17_equal_temperament Knowpia

In music, 17 equal temperament is the tempered scale derived by dividing the octave into 17 equal steps (equal frequency ratios). Each step represents a frequency ratio of ¹⁷√2, or 70.6 cents.

1 step in 17-ET

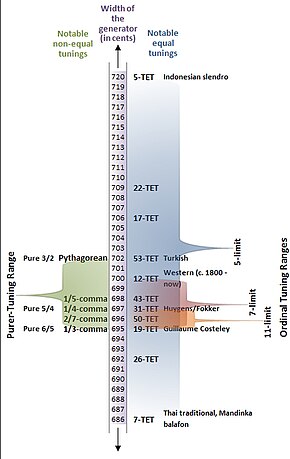
17-ET is the tuning of the regular diatonic tuning in which the tempered perfect fifth is equal to 705.88 cents, as shown in Figure 1 (look for the label "17-TET").

History and use edit

Alexander J. Ellis refers to a tuning of seventeen tones based on perfect fourths and fifths as the Arabic scale.^[2] In the thirteenth century, Middle-Eastern musician Safi al-Din Urmawi developed a theoretical system of seventeen tones to describe Arabic and Persian music, although the tones were not equally spaced. This 17-tone system remained the primary theoretical system until the development of the quarter tone scale.^{[citation needed]}

Notation edit

Notation of Easley Blackwood^[3] for 17 equal temperament: intervals are notated similarly to those they approximate and enharmonic equivalents are distinct from those of 12 equal temperament (e.g., A♯/C♭).

Easley Blackwood Jr. created a notation system where sharps and flats raised/lowered 2 steps. This yields the chromatic scale:

C, D♭, C♯, D, E♭, D♯, E, F, G♭, F♯, G, A♭, G♯, A, B♭, A♯, B, C

Quarter tone sharps and flats can also be used, yielding the following chromatic scale:

C, C

/D♭, C♯/D

, D, D

/E♭, D♯/E

, E, F, F

/G♭, F♯/G

, G, G

/A♭, G♯/A

, A, A

/B♭, A♯/B

, B, C

Interval size edit

Below are some intervals in 17-EDO compared to just.

Major chord on C in 17 equal temperament: all notes within 37 cents of just intonation (rather than 14 for 12 equal temperament)

17-et
just
12-et

I–IV–V–I chord progression in 17 equal temperament.^[4]

Whereas in 12-EDO, B♮ is 11 steps, in 17-EDO B♮ is 16 steps.

interval name	size (steps)	size (cents)	just ratio	just (cents)	error
octave	17	1200	2:1	1200	0
minor seventh	14	988.23	16:9	996	−07.77
perfect fifth	10	705.88	3:2	701.96	+03.93
septimal tritone	08	564.71	7:5	582.51	−17.81
tridecimal narrow tritone	08	564.71	18:13	563.38	+01.32
undecimal super-fourth	08	564.71	11:80	551.32	+13.39
perfect fourth	07	494.12	4:3	498.04	−03.93
septimal major third	06	423.53	9:7	435.08	−11.55
undecimal major third	06	423.53	14:11	417.51	+06.02
major third	05	352.94	5:4	386.31	−33.37
tridecimal neutral third	05	352.94	16:13	359.47	−06.53
undecimal neutral third	05	352.94	11:90	347.41	+05.53
minor third	04	282.35	6:5	315.64	−33.29
tridecimal minor third	04	282.35	13:11	289.21	−06.86
septimal minor third	04	282.35	7:6	266.87	+15.48
septimal whole tone	03	211.76	8:7	231.17	−19.41
whole tone	03	211.76	9:8	203.91	+07.85
neutral second, lesser undecimal	02	141.18	12:11	150.64	−09.46
greater tridecimal 2⁄3-tone	02	141.18	13:12	138.57	+02.60
lesser tridecimal 2⁄3-tone	02	141.18	14:13	128.30	+12.88
septimal diatonic semitone	02	141.18	15:14	119.44	+21.73
diatonic semitone	02	141.18	16:15	111.73	+29.45
septimal chromatic semitone	01	070.59	21:20	084.47	−13.88
chromatic semitone	01	070.59	25:24	070.67	−00.08

Relation to 34-ET edit

17-ET is where every other step in the 34-ET scale is included, and the others are not accessible. Conversely 34-ET is a subdivision of 17-ET.

References edit

^ Milne, Sethares & Plamondon 2007, pp. 15–32.
^ Ellis, Alexander J. (1863). "On the Temperament of Musical Instruments with Fixed Tones", Proceedings of the Royal Society of London, vol. 13. (1863–1864), pp. 404–422.
^ Blackwood, Easley (Summer 1991). "Modes and Chord Progressions in Equal Tunings". Perspectives of New Music. 29 (2): 166–200 (175). doi:10.2307/833437. JSTOR 833437.
^ Milne, Sethares & Plamondon 2007, p. 29.

Sources

Milne, Andrew; Sethares, William; Plamondon, James (Winter 2007). "Isomorphic Controllers and Dynamic Tuning: Invariant Fingering over a Tuning Continuum". Computer Music Journal. 31 (4): 15–32. doi:10.1162/comj.2007.31.4.15. S2CID 27906745.