
Summary
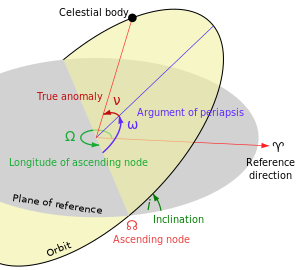
In celestial mechanics, apsidal precession (or apsidal advance)[1] is the precession (gradual rotation) of the line connecting the apsides (line of apsides) of an astronomical body's orbit. The apsides are the orbital points farthest (apoapsis) and closest (periapsis) from its primary body. The apsidal precession is the first time derivative of the argument of periapsis, one of the six main orbital elements of an orbit. Apsidal precession is considered positive when the orbit's axis rotates in the same direction as the orbital motion. An apsidal period is the time interval required for an orbit to precess through 360°,[2] which takes Earth's orbit about 112,000 years, completing a cycle and returning to the same orientation.[3]


Moon · Earth
History edit
The ancient Greek astronomer Hipparchus noted the apsidal precession of the Moon's orbit (as the revolution of the Moon's apogee with a period of approximately 8.85 years);[4] it is corrected for in the Antikythera Mechanism (circa 80 BCE) (with the supposed value of 8.88 years per full cycle, correct to within 0.34% of current measurements).[5] The precession of the solar apsides (as a motion distinct from the precession of the equinoxes), was first quantified in the second century by Ptolemy of Alexandria. He also calculated the effect of precession on movement of the heavenly bodies.[6][7][8] The apsidal precessions of the Earth and other planets are the result of a plethora of phenomena, of which a part remained difficult to account for until the 20th century when the last unidentified part of Mercury's precession was precisely explained.
Calculation edit
A variety of factors can lead to periastron precession such as general relativity, stellar quadrupole moments, mutual star–planet tidal deformations, and perturbations from other planets.[9]
- ωtotal = ωGeneral Relativity + ωquadrupole + ωtide + ωperturbations
For Mercury, the perihelion precession rate due to general relativistic effects is 43″ (arcseconds) per century. By comparison, the precession due to perturbations from the other planets in the Solar System is 532″ per century, whereas the oblateness of the Sun (quadrupole moment) causes a negligible contribution of 0.025″ per century.[10][11]
From classical mechanics, if stars and planets are considered to be purely spherical masses, then they will obey a simple 1/r2 inverse-square law, relating force to distance and hence execute closed elliptical orbits according to Bertrand's theorem. Non-spherical mass effects are caused by the application of external potential(s): the centrifugal potential of spinning bodies causes flattening between the poles and the gravity of a nearby mass raises tidal bulges. Rotational and net tidal bulges create gravitational quadrupole fields (1/r3) that lead to orbital precession.
Total apsidal precession for isolated very hot Jupiters is, considering only lowest order effects, and broadly in order of importance
- ωtotal = ωtidal perturbations + ωGeneral Relativity + ωrotational perturbations + ωrotational * + ωtidal *
with planetary tidal bulge being the dominant term, exceeding the effects of general relativity and the stellar quadrupole by more than an order of magnitude. The good resulting approximation of the tidal bulge is useful for understanding the interiors of such planets. For the shortest-period planets, the planetary interior induces precession of a few degrees per year. It is up to 19.9° per year for WASP-12b.[12][13]
Newton's theorem of revolving orbits edit
Newton derived an early theorem which attempted to explain apsidal precession. This theorem is historically notable, but it was never widely used and it proposed forces which have been found not to exist, making the theorem invalid. This theorem of revolving orbits remained largely unknown and undeveloped for over three centuries until 1995.[14] Newton proposed that variations in the angular motion of a particle can be accounted for by the addition of a force that varies as the inverse cube of distance, without affecting the radial motion of a particle.[15] Using a forerunner of the Taylor series, Newton generalized his theorem to all force laws provided that the deviations from circular orbits are small, which is valid for most planets in the Solar System.[citation needed] However, his theorem did not account for the apsidal precession of the Moon without giving up the inverse-square law of Newton's law of universal gravitation. Additionally, the rate of apsidal precession calculated via Newton's theorem of revolving orbits is not as accurate as it is for newer methods such as by perturbation theory.[citation needed]
General relativity edit
An apsidal precession of the planet Mercury was noted by Urbain Le Verrier in the mid-19th century and accounted for by Einstein's general theory of relativity.
In the 1910s, several people calculated the precession of perihelion according to special relativity. They typically obtained a value that is only 1/6 of the correct value, at 7''/year.[16][17]
Einstein showed that for a planet, the major semi-axis of its orbit being a, the eccentricity of the orbit e and the period of revolution T, then the apsidal precession due to relativistic effects, during one period of revolution in radians, is
where c is the speed of light.[18] In the case of Mercury, half of the greater axis is about 5.79×1010 m, the eccentricity of its orbit is 0.206 and the period of revolution 87.97 days or 7.6×106 s. From these and the speed of light (which is ~3×108 m/s), it can be calculated that the apsidal precession during one period of revolution is ε = 5.028×10−7 radians (2.88×10−5 degrees or 0.104″). In one hundred years, Mercury makes approximately 415 revolutions around the Sun, and thus in that time, the apsidal perihelion due to relativistic effects is approximately 43″, which corresponds almost exactly to the previously unexplained part of the measured value.
Long-term climate edit
Earth's apsidal precession slowly increases its argument of periapsis; it takes about 112,000 years for the ellipse to revolve once relative to the fixed stars.[19] Earth's polar axis, and hence the solstices and equinoxes, precess with a period of about 26,000 years in relation to the fixed stars. These two forms of 'precession' combine so that it takes between 20,800 and 29,000 years (and on average 23,000 years) for the ellipse to revolve once relative to the vernal equinox, that is, for the perihelion to return to the same date (given a calendar that tracks the seasons perfectly).[20]
This interaction between the anomalistic and tropical cycle is important in the long-term climate variations on Earth, called the Milankovitch cycles. Milankovitch cycles are central to understanding the effects of apsidal precession. An equivalent is also known on Mars.
The figure to the right illustrates the effects of precession on the northern hemisphere seasons, relative to perihelion and aphelion. Notice that the areas swept during a specific season changes through time. Orbital mechanics require that the length of the seasons be proportional to the swept areas of the seasonal quadrants, so when the orbital eccentricity is extreme, the seasons on the far side of the orbit may be substantially longer in duration.
See also edit
Notes edit
- ^ Bowler, M. G. (2010). "Apsidal advance in SS 433?". Astronomy and Astrophysics. 510 (1): A28. arXiv:0910.3536. Bibcode:2010A&A...510A..28B. doi:10.1051/0004-6361/200913471. S2CID 119289498.
- ^ Hilditch, R. W. (2001). An Introduction to Close Binary Stars. Cambridge astrophysics series. Cambridge University Press. p. 132. ISBN 9780521798006.
- ^ Buis, Alan; Laboratory, s Jet Propulsion (27 February 2020). "Milankovitch (Orbital) Cycles and Their Role in Earth's Climate – Climate Change: Vital Signs of the Planet". Climate Change: Vital Signs of the Planet. Retrieved 2 June 2023.
- ^ Jones, A., Alexander (September 1991). "The Adaptation of Babylonian Methods in Greek Numerical Astronomy" (PDF). Isis. 82 (3): 440–453. Bibcode:1991Isis...82..441J. doi:10.1086/355836. S2CID 92988054. Archived from the original (PDF) on 4 March 2016. Retrieved 7 August 2014.
- ^ Freeth, Tony; Bitsakis, Yanis; Moussas, Xenophon; Seiradakis, John. H.; Tselikas, A.; Mangou, H.; Zafeiropoulou, M.; Hadland, R.; et al. (30 November 2006). "Decoding the ancient Greek astronomical calculator known as the Antikythera Mechanism" (PDF). Nature. 444 Supplement (7119): 587–91. Bibcode:2006Natur.444..587F. doi:10.1038/nature05357. PMID 17136087. S2CID 4424998. Archived from the original (PDF) on 20 July 2015. Retrieved 20 May 2014.
- ^ Toomer, G. J. (1969), "The Solar Theory of az-Zarqāl: A History of Errors", Centaurus, 14 (1): 306–336, Bibcode:1969Cent...14..306T, doi:10.1111/j.1600-0498.1969.tb00146.x, at pp. 314–317.
- ^ "Ptolemaic Astronomy in the Middle Ages". princeton.edu. Retrieved 21 October 2022.
- ^ C. Philipp E. Nothaft (2017). "Criticism of trepidation models and advocacy of uniform precession in medieval Latin astronomy". Archive for History of Exact Sciences. 71 (3): 211–244. doi:10.1007/s00407-016-0184-1. S2CID 253894382.
- ^ David M. Kipping (8 August 2011). The Transits of Extrasolar Planets with Moons. Springer. pp. 84–. ISBN 978-3-642-22269-6. Retrieved 27 August 2013.
- ^ Kane, S. R.; Horner, J.; von Braun, K. (2012). "Cyclic Transit Probabilities of Long-period Eccentric Planets due to Periastron Precession". The Astrophysical Journal. 757 (1): 105. arXiv:1208.4115. Bibcode:2012ApJ...757..105K. doi:10.1088/0004-637x/757/1/105. S2CID 54193207.
- ^ Richard Fitzpatrick (30 June 2012). An Introduction to Celestial Mechanics. Cambridge University Press. p. 69. ISBN 978-1-107-02381-9. Retrieved 26 August 2013.
- ^ Ragozzine, D.; Wolf, A. S. (2009). "Probing the interiors of very hot Jupiters using transit light curves". The Astrophysical Journal. 698 (2): 1778–1794. arXiv:0807.2856. Bibcode:2009ApJ...698.1778R. doi:10.1088/0004-637x/698/2/1778. S2CID 29915528.
- ^ Michael Perryman (26 May 2011). The Exoplanet Handbook. Cambridge University Press. pp. 133–. ISBN 978-1-139-49851-7. Retrieved 26 August 2013.
- ^ Chandrasekhar, p. 183.
- ^ Lynden-Bell, D.; Jin, S. (1 May 2008). "Analytic central orbits and their transformation group". Monthly Notices of the Royal Astronomical Society. 386 (1): 245–260. arXiv:0711.3491. Bibcode:2008MNRAS.386..245L. doi:10.1111/j.1365-2966.2008.13018.x. ISSN 0035-8711. S2CID 15451037.
- ^ McDonald, Kirk T. "Special Relativity and the Precession of the Perihelion." JH Lab., Princeton University (2023).
- ^ Goldstein, Herbert; Poole, Charles P.; Safko, John L. (2008). Classical mechanics (3. ed., [Nachdr.] ed.). San Francisco Munich: Addison Wesley. Chapter 7, Exercise 27, Page 332. ISBN 978-0-201-65702-9.
- ^ Hawking, Stephen (2002). On the Shoulders of Giants : the Great Works of Physics and Astronomy. Philadelphia, Pennsylvania, USA: Running Press. pp. der Physik. ISBN 0-7624-1348-4.
- ^ van den Heuvel, E. P. J. (1966). "On the Precession as a Cause of Pleistocene Variations of the Atlantic Ocean Water Temperatures". Geophysical Journal International. 11 (3): 323–336. Bibcode:1966GeoJ...11..323V. doi:10.1111/j.1365-246X.1966.tb03086.x.
- ^ The Seasons and the Earth's Orbit, United States Naval Observatory, archived from the original on 2 August 2013, retrieved 16 August 2013


