
Summary
In geometry, calculating the area of a triangle is an elementary problem encountered often in many different situations. The best known and simplest formula is where b is the length of the base of the triangle, and h is the height or altitude of the triangle. The term "base" denotes any side, and "height" denotes the length of a perpendicular from the vertex opposite the base onto the line containing the base. Euclid proved that the area of a triangle is half that of a parallelogram with the same base and height in his book Elements in 300 BCE.[1] In 499 CE Aryabhata, used this illustrated method in the Aryabhatiya (section 2.6).[2]

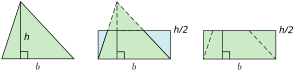
Although simple, this formula is only useful if the height can be readily found, which is not always the case. For example, the land surveyor of a triangular field might find it relatively easy to measure the length of each side, but relatively difficult to construct a 'height'. Various methods may be used in practice, depending on what is known about the triangle. Other frequently used formulas for the area of a triangle use trigonometry, side lengths (Heron's formula), vectors, coordinates, line integrals, Pick's theorem, or other properties.[3]
History edit
Heron of Alexandria found what is known as Heron's formula for the area of a triangle in terms of its sides, and a proof can be found in his book, Metrica, written around 60 CE. It has been suggested that Archimedes knew the formula over two centuries earlier,[4] and since Metrica is a collection of the mathematical knowledge available in the ancient world, it is possible that the formula predates the reference given in that work.[5] In 300 BCE Greek mathematician Euclid proved that the area of a triangle is half that of a parallelogram with the same base and height in his book Elements of Geometry.[6]
In 499 Aryabhata, a great mathematician-astronomer from the classical age of Indian mathematics and Indian astronomy, expressed the area of a triangle as one-half the base times the height in the Aryabhatiya (section 2.6).
A formula equivalent to Heron's was discovered by the Chinese independently of the Greeks. It was published in 1247 in Shushu Jiuzhang ("Mathematical Treatise in Nine Sections"), written by Qin Jiushao.
Using trigonometry edit
The height of a triangle can be found through the application of trigonometry.
- Knowing SAS (side-angle-side)
Using the labels in the image on the right, the altitude is h = a sin . Substituting this in the formula derived above, the area of the triangle can be expressed as:
(where α is the interior angle at A, β is the interior angle at B, is the interior angle at C and c is the line AB).
Furthermore, since sin α = sin (π − α) = sin (β + ), and similarly for the other two angles:
- Knowing AAS (angle-angle-side)
and analogously if the known side is a or c.
- Knowing ASA (angle-side-angle)
and analogously if the known side is b or c.[7]
Using side lengths (Heron's formula) edit
The shape of the triangle is determined by the lengths of the sides. Therefore, the area can also be derived from the lengths of the sides. By Heron's formula:
where is the semiperimeter, or half of the triangle's perimeter.
Three other equivalent ways of writing Heron's formula are
Formulas resembling Heron's formula edit
Three formulas have the same structure as Heron's formula but are expressed in terms of different variables. First, denoting the medians from sides a, b, and c respectively as ma, mb, and mc and their semi-sum (ma + mb + mc)/2 as σ, we have[8]
Next, denoting the altitudes from sides a, b, and c respectively as ha, hb, and hc, and denoting the semi-sum of the reciprocals of the altitudes as we have[9]
And denoting the semi-sum of the angles' sines as S = [(sin α) + (sin β) + (sin γ)]/2, we have[10]
where D is the diameter of the circumcircle:
Using vectors edit
The area of triangle ABC is half of the area of a parallelogram:
The area of a parallelogram embedded in a three-dimensional Euclidean space can be calculated using vectors. Let vectors AB and AC point respectively from A to B and from A to C. The area of parallelogram ABDC is then
which is the magnitude of the cross product of vectors AB and AC.
The area of triangle ABC can also be expressed in terms of dot products as follows:
In two-dimensional Euclidean space, expressing vector AB as a free vector in Cartesian space equal to (x1,y1) and AC as (x2,y2), this can be rewritten as:
Using coordinates edit
If vertex A is located at the origin (0, 0) of a Cartesian coordinate system and the coordinates of the other two vertices are given by B = (xB, yB) and C = (xC, yC), then the area can be computed as 1⁄2 times the absolute value of the determinant
For three general vertices, the equation is:
which can be written as
If the points are labeled sequentially in the counterclockwise direction, the above determinant expressions are positive and the absolute value signs can be omitted.[11] The above formula is known as the shoelace formula or the surveyor's formula.
If we locate the vertices in the complex plane and denote them in counterclockwise sequence as a = xA + yAi, b = xB + yBi, and c = xC + yCi, and denote their complex conjugates as , , and , then the formula
is equivalent to the shoelace formula.
In three dimensions, the area of a general triangle A = (xA, yA, zA), B = (xB, yB, zB) and C = (xC, yC, zC) is the Pythagorean sum of the areas of the respective projections on the three principal planes (i.e. x = 0, y = 0 and z = 0):
Using line integrals edit
The area within any closed curve, such as a triangle, is given by the line integral around the curve of the algebraic or signed distance of a point on the curve from an arbitrary oriented straight line L. Points to the right of L as oriented are taken to be at negative distance from L, while the weight for the integral is taken to be the component of arc length parallel to L rather than arc length itself.
This method is well suited to computation of the area of an arbitrary polygon. Taking L to be the x-axis, the line integral between consecutive vertices (xi,yi) and (xi+1,yi+1) is given by the base times the mean height, namely (xi+1 − xi)(yi + yi+1)/2. The sign of the area is an overall indicator of the direction of traversal, with negative area indicating counterclockwise traversal. The area of a triangle then falls out as the case of a polygon with three sides.
While the line integral method has in common with other coordinate-based methods the arbitrary choice of a coordinate system, unlike the others it makes no arbitrary choice of vertex of the triangle as origin or of side as base. Furthermore, the choice of coordinate system defined by L commits to only two degrees of freedom rather than the usual three, since the weight is a local distance (e.g. xi+1 − xi in the above) whence the method does not require choosing an axis normal to L.
When working in polar coordinates it is not necessary to convert to Cartesian coordinates to use line integration, since the line integral between consecutive vertices (ri,θi) and (ri+1,θi+1) of a polygon is given directly by riri+1sin(θi+1 − θi)/2. This is valid for all values of θ, with some decrease in numerical accuracy when |θ| is many orders of magnitude greater than π. With this formulation negative area indicates clockwise traversal, which should be kept in mind when mixing polar and cartesian coordinates. Just as the choice of y-axis (x = 0) is immaterial for line integration in cartesian coordinates, so is the choice of zero heading (θ = 0) immaterial here.
Using Pick's theorem edit
See Pick's theorem for a technique for finding the area of any arbitrary lattice polygon (one drawn on a grid with vertically and horizontally adjacent lattice points at equal distances, and with vertices on lattice points).
The theorem states:
where is the number of internal lattice points and B is the number of lattice points lying on the border of the polygon.
Other area formulas edit
Numerous other area formulas exist, such as
where r is the inradius, and s is the semiperimeter (in fact, this formula holds for all tangential polygons), and[12]: Lemma 2
where are the radii of the excircles tangent to sides a, b, c respectively.
We also have
and[13]
for circumdiameter D; and[14]
for angle α ≠ 90°.
The area can also be expressed as[15]
In 1885, Baker[16] gave a collection of over a hundred distinct area formulas for the triangle. These include:
for circumradius (radius of the circumcircle) R, and
Upper bound on the area edit
The area T of any triangle with perimeter p satisfies
with equality holding if and only if the triangle is equilateral.[17][18]: 657
Other upper bounds on the area T are given by[19]: p.290
and
both again holding if and only if the triangle is equilateral.
Bisecting the area edit
There are infinitely many lines that bisect the area of a triangle.[20] Three of them are the medians, which are the only area bisectors that go through the centroid. Three other area bisectors are parallel to the triangle's sides.
Any line through a triangle that splits both the triangle's area and its perimeter in half goes through the triangle's incenter. There can be one, two, or three of these for any given triangle.
See also edit
References edit
- ^ "Euclid's Proof of the Pythagorean Theorem | Synaptic". Central College. Retrieved 2023-07-12.
- ^ The Āryabhaṭīya by Āryabhaṭa (translated into English by Walter Eugene Clark, 1930) hosted online by the Internet Archive.
- ^ Weisstein, Eric W. "Triangle area". MathWorld.
- ^ Heath, Thomas L. (1921). A History of Greek Mathematics (Vol II). Oxford University Press. pp. 321–323.
- ^ Weisstein, Eric W. "Heron's Formula". MathWorld.
- ^ "Euclid's Proof of the Pythagorean Theorem | Synaptic". Central College. Retrieved 2023-07-12.
- ^ Weisstein, Eric W. "Triangle". MathWorld.
- ^ Benyi, Arpad, "A Heron-type formula for the triangle," Mathematical Gazette 87, July 2003, 324–326.
- ^ Mitchell, Douglas W., "A Heron-type formula for the reciprocal area of a triangle," Mathematical Gazette 89, November 2005, 494.
- ^ Mitchell, Douglas W., "A Heron-type area formula in terms of sines," Mathematical Gazette 93, March 2009, 108–109.
- ^ Bart Braden (1986). "The Surveyor's Area Formula" (PDF). The College Mathematics Journal. 17 (4): 326–337. doi:10.2307/2686282. JSTOR 2686282. Archived from the original (PDF) on 5 November 2003. Retrieved 5 January 2012.
- ^ "Sa ́ndor Nagydobai Kiss, "A Distance Property of the Feuerbach Point and Its Extension", Forum Geometricorum 16, 2016, 283–290" (PDF).
- ^ "Circumradius". AoPSWiki. Archived from the original on 20 June 2013. Retrieved 26 July 2012.
- ^ Mitchell, Douglas W., "The area of a quadrilateral," Mathematical Gazette 93, July 2009, 306–309.
- ^ Pathan, Alex, and Tony Collyer, "Area properties of triangles revisited," Mathematical Gazette 89, November 2005, 495–497.
- ^ Baker, Marcus, "A collection of formulae for the area of a plane triangle," Annals of Mathematics, part 1 in vol. 1(6), January 1885, 134–138; part 2 in vol. 2(1), September 1885, 11–18. The formulas given here are #9, #39a, #39b, #42, and #49. The reader is advised that several of the formulas in this source are not correct.
- ^ Chakerian, G.D. "A Distorted View of Geometry." Ch. 7 in Mathematical Plums (R. Honsberger, editor). Washington, DC: Mathematical Association of America, 1979: 147.
- ^ Rosenberg, Steven; Spillane, Michael; and Wulf, Daniel B. "Heron triangles and moduli spaces", Mathematics Teacher 101, May 2008, 656–663.
- ^ Posamentier, Alfred S., and Lehmann, Ingmar, The Secrets of Triangles, Prometheus Books, 2012.
- ^ Dunn, J.A., and Pretty, J.E., "Halving a triangle," Mathematical Gazette 56, May 1972, 105–108.




