
Summary
In mathematics, the associative property[1] is a property of some binary operations, which means that rearranging the parentheses in an expression will not change the result. In propositional logic, associativity is a valid rule of replacement for expressions in logical proofs.
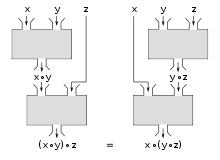 A visual graph representing associative operations; | |
| Type | Law, rule of replacement |
|---|---|
| Field | |
| Symbolic statement |
|
Within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not changed. That is (after rewriting the expression with parentheses and in infix notation if necessary), rearranging the parentheses in such an expression will not change its value. Consider the following equations:
Even though the parentheses were rearranged on each line, the values of the expressions were not altered. Since this holds true when performing addition and multiplication on any real numbers, it can be said that "addition and multiplication of real numbers are associative operations".
Associativity is not the same as commutativity, which addresses whether the order of two operands affects the result. For example, the order does not matter in the multiplication of real numbers, that is, a × b = b × a, so we say that the multiplication of real numbers is a commutative operation. However, operations such as function composition and matrix multiplication are associative, but not (generally) commutative.
Associative operations are abundant in mathematics; in fact, many algebraic structures (such as semigroups and categories) explicitly require their binary operations to be associative.
However, many important and interesting operations are non-associative; some examples include subtraction, exponentiation, and the vector cross product. In contrast to the theoretical properties of real numbers, the addition of floating point numbers in computer science is not associative, and the choice of how to associate an expression can have a significant effect on rounding error.
Definition edit
Formally, a binary operation ∗ on a set S is called associative if it satisfies the associative law:
Here, ∗ is used to replace the symbol of the operation, which may be any symbol, and even the absence of symbol (juxtaposition) as for multiplication.
The associative law can also be expressed in functional notation thus: f(f(x, y), z) = f(x, f(y, z)).
Generalized associative law edit
If a binary operation is associative, repeated application of the operation produces the same result regardless of how valid pairs of parentheses are inserted in the expression.[2] This is called the generalized associative law.
The number of possible bracketings is just the Catalan number, Cn, for n operations on n+1 values. For instance, a product of 3 operations on 4 elements may be written (ignoring permutations of the arguments), in C3 = 5 possible ways:
- ((ab)c)d
- (ab)(cd)
- (a(bc))d
- a((bc)d)
- a(b(cd))
If the product operation is associative, the generalized associative law says that all these expressions will yield the same result. So unless the expression with omitted parentheses already has a different meaning (see below), the parentheses can be considered unnecessary and "the" product can be written unambiguously as
As the number of elements increases, the number of possible ways to insert parentheses grows quickly, but they remain unnecessary for disambiguation.
An example where this does not work is the logical biconditional ↔. It is associative; thus, A ↔ (B ↔ C) is equivalent to (A ↔ B) ↔ C, but A ↔ B ↔ C most commonly means (A ↔ B) and (B ↔ C), which is not equivalent.
Examples edit
Some examples of associative operations include the following.
- The concatenation of the three strings
"hello"," ","world"can be computed by concatenating the first two strings (giving"hello ") and appending the third string ("world"), or by joining the second and third string (giving" world") and concatenating the first string ("hello") with the result. The two methods produce the same result; string concatenation is associative (but not commutative). - In arithmetic, addition and multiplication of real numbers are associative; i.e.,
Because of associativity, the grouping parentheses can be omitted without ambiguity.
- The trivial operation x ∗ y = x (that is, the result is the first argument, no matter what the second argument is) is associative but not commutative. Likewise, the trivial operation x ∘ y = y (that is, the result is the second argument, no matter what the first argument is) is associative but not commutative.
- Addition and multiplication of complex numbers and quaternions are associative. Addition of octonions is also associative, but multiplication of octonions is non-associative.
- The greatest common divisor and least common multiple functions act associatively.
- Taking the intersection or the union of sets:
- If M is some set and S denotes the set of all functions from M to M, then the operation of function composition on S is associative:
- Slightly more generally, given four sets M, N, P and Q, with h : M → N, g : N → P, and f : P → Q, then
as before. In short, composition of maps is always associative.
- In category theory, composition of morphisms is associative by definition. Associativity of functors and natural transformations follows from associativity of morphisms.
- Consider a set with three elements, A, B, and C. The following operation:
is associative. Thus, for example, A(BC) = (AB)C = A. This operation is not commutative.× A B C A A A A B A B C C A A A - Because matrices represent linear functions, and matrix multiplication represents function composition, one can immediately conclude that matrix multiplication is associative.[3]
- For real numbers (and for any totally ordered set), the minimum and maximum operation is associative:
Propositional logic edit
Rule of replacement edit
In standard truth-functional propositional logic, association,[4][5] or associativity[6] are two valid rules of replacement. The rules allow one to move parentheses in logical expressions in logical proofs. The rules (using logical connectives notation) are:
and
where " " is a metalogical symbol representing "can be replaced in a proof with".
Truth functional connectives edit
Associativity is a property of some logical connectives of truth-functional propositional logic. The following logical equivalences demonstrate that associativity is a property of particular connectives. The following (and their converses, since ↔ is commutative) are truth-functional tautologies.[citation needed]
- Associativity of disjunction
- Associativity of conjunction
- Associativity of equivalence
Joint denial is an example of a truth functional connective that is not associative.
Non-associative operation edit
A binary operation on a set S that does not satisfy the associative law is called non-associative. Symbolically,
For such an operation the order of evaluation does matter. For example:
Also although addition is associative for finite sums, it is not associative inside infinite sums (series). For example,
Some non-associative operations are fundamental in mathematics. They appear often as the multiplication in structures called non-associative algebras, which have also an addition and a scalar multiplication. Examples are the octonions and Lie algebras. In Lie algebras, the multiplication satisfies Jacobi identity instead of the associative law; this allows abstracting the algebraic nature of infinitesimal transformations.
Other examples are quasigroup, quasifield, non-associative ring, and commutative non-associative magmas.
Nonassociativity of floating point calculation edit
In mathematics, addition and multiplication of real numbers is associative. By contrast, in computer science, the addition and multiplication of floating point numbers is not associative, as rounding errors are introduced when dissimilar-sized values are joined together.[7]
To illustrate this, consider a floating point representation with a 4-bit mantissa:
Even though most computers compute with 24 or 53 bits of mantissa,[8] this is an important source of rounding error, and approaches such as the Kahan summation algorithm are ways to minimise the errors. It can be especially problematic in parallel computing.[9][10]
Notation for non-associative operations edit
In general, parentheses must be used to indicate the order of evaluation if a non-associative operation appears more than once in an expression (unless the notation specifies the order in another way, like ). However, mathematicians agree on a particular order of evaluation for several common non-associative operations. This is simply a notational convention to avoid parentheses.
A left-associative operation is a non-associative operation that is conventionally evaluated from left to right, i.e.,
while a right-associative operation is conventionally evaluated from right to left:
Both left-associative and right-associative operations occur. Left-associative operations include the following:
This notation can be motivated by the currying isomorphism, which enables partial application.
Right-associative operations include the following:
- Exponentiation of real numbers in superscript notation
-
Exponentiation is commonly used with brackets or right-associatively because a repeated left-associative exponentiation operation is of little use. Repeated powers would mostly be rewritten with multiplication:
-
Formatted correctly, the superscript inherently behaves as a set of parentheses; e.g. in the expression the addition is performed before the exponentiation despite there being no explicit parentheses wrapped around it. Thus given an expression such as , the full exponent of the base is evaluated first. However, in some contexts, especially in handwriting, the difference between , and can be hard to see. In such a case, right-associativity is usually implied.
- Function definition
-
Using right-associative notation for these operations can be motivated by the Curry–Howard correspondence and by the currying isomorphism.
Non-associative operations for which no conventional evaluation order is defined include the following.
- Exponentiation of real numbers in infix notation[16]
- Knuth's up-arrow operators
- Taking the cross product of three vectors
- Taking the pairwise average of real numbers
- Taking the relative complement of sets
- .
(Compare material nonimplication in logic.)
History edit
William Rowan Hamilton seems to have coined the term "associative property"[17] around 1844, a time when he was contemplating the non-associative algebra of the octonions he had learned about from John T. Graves.[18]
See also edit
- Light's associativity test
- Telescoping series, the use of addition associativity for cancelling terms in an infinite series
- A semigroup is a set with an associative binary operation.
- Commutativity and distributivity are two other frequently discussed properties of binary operations.
- Power associativity, alternativity, flexibility and N-ary associativity are weak forms of associativity.
- Moufang identities also provide a weak form of associativity.
References edit
- ^
Hungerford, Thomas W. (1974). Algebra (1st ed.). Springer. p. 24. ISBN 978-0387905181.
Definition 1.1 (i) a(bc) = (ab)c for all a, b, c in G.
- ^ Durbin, John R. (1992). Modern Algebra: an Introduction (3rd ed.). New York: Wiley. p. 78. ISBN 978-0-471-51001-7.
If are elements of a set with an associative operation, then the product is unambiguous; this is, the same element will be obtained regardless of how parentheses are inserted in the product.
- ^ "Matrix product associativity". Khan Academy. Retrieved 5 June 2016.
- ^ Moore, Brooke Noel; Parker, Richard (2017). Critical Thinking (12th ed.). New York: McGraw-Hill Education. p. 321. ISBN 9781259690877.
- ^ Copi, Irving M.; Cohen, Carl; McMahon, Kenneth (2014). Introduction to Logic (14th ed.). Essex: Pearson Education. p. 387. ISBN 9781292024820.
- ^ Hurley, Patrick J.; Watson, Lori (2016). A Concise Introduction to Logic (13th ed.). Boston: Cengage Learning. p. 427. ISBN 9781305958098.
- ^ Knuth, Donald, The Art of Computer Programming, Volume 3, section 4.2.2
- ^ IEEE Computer Society (29 August 2008). IEEE Standard for Floating-Point Arithmetic. doi:10.1109/IEEESTD.2008.4610935. ISBN 978-0-7381-5753-5. IEEE Std 754-2008.
- ^ Villa, Oreste; Chavarría-mir, Daniel; Gurumoorthi, Vidhya; Márquez, Andrés; Krishnamoorthy, Sriram, Effects of Floating-Point non-Associativity on Numerical Computations on Massively Multithreaded Systems (PDF), archived from the original (PDF) on 15 February 2013, retrieved 8 April 2014
- ^ Goldberg, David (March 1991). "What Every Computer Scientist Should Know About Floating-Point Arithmetic" (PDF). ACM Computing Surveys. 23 (1): 5–48. doi:10.1145/103162.103163. S2CID 222008826. Archived (PDF) from the original on 2022-05-19. Retrieved 20 January 2016.
- ^ George Mark Bergman "Order of arithmetic operations"
- ^ "The Order of Operations". Education Place.
- ^ "The Order of Operations", timestamp 5m40s. Khan Academy.
- ^ "Using Order of Operations and Exploring Properties" Archived 2022-07-16 at the Wayback Machine, section 9. Virginia Department of Education.
- ^ Bronstein, de:Taschenbuch der Mathematik, pages 115-120, chapter: 2.4.1.1, ISBN 978-3-8085-5673-3
- ^ Exponentiation Associativity and Standard Math Notation Codeplea. 23 August 2016. Retrieved 20 September 2016.
- ^ Hamilton, W.R. (1844–1850). "On quaternions or a new system of imaginaries in algebra". David R. Wilkins collection. Philosophical Magazine. Trinity College Dublin.
- ^ Baez, John C. (2002). "The Octonions" (PDF). Bulletin of the American Mathematical Society. 39 (2): 145–205. arXiv:math/0105155. doi:10.1090/S0273-0979-01-00934-X. ISSN 0273-0979. MR 1886087. S2CID 586512.







