Cantor_distribution Knowpia

Cantor
	Cumulative distribution function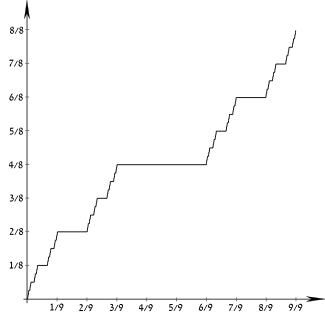
Parameters	none
Support	Cantor set, a subset of [0,1]
PMF	none
CDF	Cantor function
Mean	1/2
Median	anywhere in [1/3, 2/3]
Mode	n/a
Variance	1/8
Skewness	0
Excess kurtosis	−8/5
MGF
CF

The Cantor distribution is the probability distribution whose cumulative distribution function is the Cantor function.

This distribution has neither a probability density function nor a probability mass function, since although its cumulative distribution function is a continuous function, the distribution is not absolutely continuous with respect to Lebesgue measure, nor does it have any point-masses. It is thus neither a discrete nor an absolutely continuous probability distribution, nor is it a mixture of these. Rather it is an example of a singular distribution.

Its cumulative distribution function is continuous everywhere but horizontal almost everywhere, so is sometimes referred to as the Devil's staircase, although that term has a more general meaning.

Characterization edit

The support of the Cantor distribution is the Cantor set, itself the intersection of the (countably infinitely many) sets:

{\begin{aligned}C_{0}={}&[0,1]\\[8pt]C_{1}={}&[0,1/3]\cup [2/3,1]\\[8pt]C_{2}={}&[0,1/9]\cup [2/9,1/3]\cup [2/3,7/9]\cup [8/9,1]\\[8pt]C_{3}={}&[0,1/27]\cup [2/27,1/9]\cup [2/9,7/27]\cup [8/27,1/3]\cup \\[4pt]{}&[2/3,19/27]\cup [20/27,7/9]\cup [8/9,25/27]\cup [26/27,1]\\[8pt]C_{4}={}&[0,1/81]\cup [2/81,1/27]\cup [2/27,7/81]\cup [8/81,1/9]\cup [2/9,19/81]\cup [20/81,7/27]\cup \\[4pt]&[8/27,25/81]\cup [26/81,1/3]\cup [2/3,55/81]\cup [56/81,19/27]\cup [20/27,61/81]\cup \\[4pt]&[62/81,21/27]\cup [8/9,73/81]\cup [74/81,25/27]\cup [26/27,79/81]\cup [80/81,1]\\[8pt]C_{5}={}&\cdots \end{aligned}}

The Cantor distribution is the unique probability distribution for which for any C_t (t ∈ { 0, 1, 2, 3, ... }), the probability of a particular interval in C_t containing the Cantor-distributed random variable is identically 2^−t on each one of the 2^t intervals.

Moments edit

It is easy to see by symmetry and being bounded that for a random variable X having this distribution, its expected value E(X) = 1/2, and that all odd central moments of X are 0.

The law of total variance can be used to find the variance var(X), as follows. For the above set C₁, let Y = 0 if X ∈ [0,1/3], and 1 if X ∈ [2/3,1]. Then:

{\begin{aligned}\operatorname {var} (X)&=\operatorname {E} (\operatorname {var} (X\mid Y))+\operatorname {var} (\operatorname {E} (X\mid Y))\\&={\frac {1}{9}}\operatorname {var} (X)+\operatorname {var} \left\{{\begin{matrix}1/6&{\mbox{with probability}}\ 1/2\\5/6&{\mbox{with probability}}\ 1/2\end{matrix}}\right\}\\&={\frac {1}{9}}\operatorname {var} (X)+{\frac {1}{9}}\end{aligned}}

From this we get:

\operatorname {var} (X)={\frac {1}{8}}.

A closed-form expression for any even central moment can be found by first obtaining the even cumulants^[1]

\kappa _{2n}={\frac {2^{2n-1}(2^{2n}-1)B_{2n}}{n\,(3^{2n}-1)}},\,\!

where B_2n is the 2nth Bernoulli number, and then expressing the moments as functions of the cumulants.

References edit

^ Morrison, Kent (1998-07-23). "Random Walks with Decreasing Steps" (PDF). Department of Mathematics, California Polytechnic State University. Archived from the original (PDF) on 2015-12-02. Retrieved 2007-02-16.

Summary

Characterization edit

Moments edit

References edit

Further reading edit