
Summary
In mathematics, the distributive property of binary operations is a generalization of the distributive law, which asserts that the equality is always true in elementary algebra. For example, in elementary arithmetic, one has Therefore, one would say that multiplication distributes over addition.
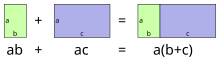 Visualization of distributive law for positive numbers | |
| Type | Law, rule of replacement |
|---|---|
| Field | |
| Symbolic statement |
|
This basic property of numbers is part of the definition of most algebraic structures that have two operations called addition and multiplication, such as complex numbers, polynomials, matrices, rings, and fields. It is also encountered in Boolean algebra and mathematical logic, where each of the logical and (denoted ) and the logical or (denoted ) distributes over the other.
Definition
editGiven a set and two binary operators and on
- the operation is left-distributive over (or with respect to) if, given any elements of
- the operation is right-distributive over if, given any elements of
- and the operation is distributive over if it is left- and right-distributive.[1]
When is commutative, the three conditions above are logically equivalent.
Meaning
editThe operators used for examples in this section are those of the usual addition and multiplication
If the operation denoted is not commutative, there is a distinction between left-distributivity and right-distributivity:
In either case, the distributive property can be described in words as:
To multiply a sum (or difference) by a factor, each summand (or minuend and subtrahend) is multiplied by this factor and the resulting products are added (or subtracted).
If the operation outside the parentheses (in this case, the multiplication) is commutative, then left-distributivity implies right-distributivity and vice versa, and one talks simply of distributivity.
One example of an operation that is "only" right-distributive is division, which is not commutative: In this case, left-distributivity does not apply:
The distributive laws are among the axioms for rings (like the ring of integers) and fields (like the field of rational numbers). Here multiplication is distributive over addition, but addition is not distributive over multiplication. Examples of structures with two operations that are each distributive over the other are Boolean algebras such as the algebra of sets or the switching algebra.
Multiplying sums can be put into words as follows: When a sum is multiplied by a sum, multiply each summand of a sum with each summand of the other sum (keeping track of signs) then add up all of the resulting products.
Examples
editReal numbers
editIn the following examples, the use of the distributive law on the set of real numbers is illustrated. When multiplication is mentioned in elementary mathematics, it usually refers to this kind of multiplication. From the point of view of algebra, the real numbers form a field, which ensures the validity of the distributive law.
- First example (mental and written multiplication)
- During mental arithmetic, distributivity is often used unconsciously: Thus, to calculate in one's head, one first multiplies and and add the intermediate results. Written multiplication is also based on the distributive law.
- Second example (with variables)
- Third example (with two sums)
- Here the distributive law was applied twice, and it does not matter which bracket is first multiplied out.
- Fourth example
- Here the distributive law is applied the other way around compared to the previous examples. Consider Since the factor occurs in all summands, it can be factored out. That is, due to the distributive law one obtains
Matrices
editThe distributive law is valid for matrix multiplication. More precisely, for all -matrices and -matrices as well as for all -matrices and -matrices Because the commutative property does not hold for matrix multiplication, the second law does not follow from the first law. In this case, they are two different laws.
Other examples
edit- Multiplication of ordinal numbers, in contrast, is only left-distributive, not right-distributive.
- The cross product is left- and right-distributive over vector addition, though not commutative.
- The union of sets is distributive over intersection, and intersection is distributive over union.
- Logical disjunction ("or") is distributive over logical conjunction ("and"), and vice versa.
- For real numbers (and for any totally ordered set), the maximum operation is distributive over the minimum operation, and vice versa:
- For integers, the greatest common divisor is distributive over the least common multiple, and vice versa:
- For real numbers, addition distributes over the maximum operation, and also over the minimum operation:
- For binomial multiplication, distribution is sometimes referred to as the FOIL Method[2] (First terms Outer Inner and Last ) such as:
- In all semirings, including the complex numbers, the quaternions, polynomials, and matrices, multiplication distributes over addition:
- In all algebras over a field, including the octonions and other non-associative algebras, multiplication distributes over addition.
Propositional logic
editRule of replacement
editIn standard truth-functional propositional logic, distribution[3][4] in logical proofs uses two valid rules of replacement to expand individual occurrences of certain logical connectives, within some formula, into separate applications of those connectives across subformulas of the given formula. The rules are where " ", also written is a metalogical symbol representing "can be replaced in a proof with" or "is logically equivalent to".
Truth functional connectives
editDistributivity is a property of some logical connectives of truth-functional propositional logic. The following logical equivalences demonstrate that distributivity is a property of particular connectives. The following are truth-functional tautologies.
- Double distribution
Distributivity and rounding
editIn approximate arithmetic, such as floating-point arithmetic, the distributive property of multiplication (and division) over addition may fail because of the limitations of arithmetic precision. For example, the identity fails in decimal arithmetic, regardless of the number of significant digits. Methods such as banker's rounding may help in some cases, as may increasing the precision used, but ultimately some calculation errors are inevitable.
In rings and other structures
editDistributivity is most commonly found in semirings, notably the particular cases of rings and distributive lattices.
A semiring has two binary operations, commonly denoted and and requires that must distribute over
A ring is a semiring with additive inverses.
A lattice is another kind of algebraic structure with two binary operations, If either of these operations distributes over the other (say distributes over ), then the reverse also holds ( distributes over ), and the lattice is called distributive. See also Distributivity (order theory).
A Boolean algebra can be interpreted either as a special kind of ring (a Boolean ring) or a special kind of distributive lattice (a Boolean lattice). Each interpretation is responsible for different distributive laws in the Boolean algebra.
Similar structures without distributive laws are near-rings and near-fields instead of rings and division rings. The operations are usually defined to be distributive on the right but not on the left.
Generalizations
edit
In several mathematical areas, generalized distributivity laws are considered. This may involve the weakening of the above conditions or the extension to infinitary operations. Especially in order theory one finds numerous important variants of distributivity, some of which include infinitary operations, such as the infinite distributive law; others being defined in the presence of only one binary operation, such as the according definitions and their relations are given in the article distributivity (order theory). This also includes the notion of a completely distributive lattice.
In the presence of an ordering relation, one can also weaken the above equalities by replacing by either or Naturally, this will lead to meaningful concepts only in some situations. An application of this principle is the notion of sub-distributivity as explained in the article on interval arithmetic.
In category theory, if and are monads on a category a distributive law is a natural transformation such that is a lax map of monads and is a colax map of monads This is exactly the data needed to define a monad structure on : the multiplication map is and the unit map is See: distributive law between monads.
A generalized distributive law has also been proposed in the area of information theory.
Antidistributivity
editThe ubiquitous identity that relates inverses to the binary operation in any group, namely which is taken as an axiom in the more general context of a semigroup with involution, has sometimes been called an antidistributive property (of inversion as a unary operation).[5]
In the context of a near-ring, which removes the commutativity of the additively written group and assumes only one-sided distributivity, one can speak of (two-sided) distributive elements but also of antidistributive elements. The latter reverse the order of (the non-commutative) addition; assuming a left-nearring (i.e. one which all elements distribute when multiplied on the left), then an antidistributive element reverses the order of addition when multiplied to the right: [6]
In the study of propositional logic and Boolean algebra, the term antidistributive law is sometimes used to denote the interchange between conjunction and disjunction when implication factors over them:[7]
These two tautologies are a direct consequence of the duality in De Morgan's laws.
Notes
edit- ^ Distributivity of Binary Operations from Mathonline
- ^ Kim Steward (2011) Multiplying Polynomials from Virtual Math Lab at West Texas A&M University
- ^ Elliott Mendelson (1964) Introduction to Mathematical Logic, page 21, D. Van Nostrand Company
- ^ Alfred Tarski (1941) Introduction to Logic, page 52, Oxford University Press
- ^ Chris Brink; Wolfram Kahl; Gunther Schmidt (1997). Relational Methods in Computer Science. Springer. p. 4. ISBN 978-3-211-82971-4.
- ^ Celestina Cotti Ferrero; Giovanni Ferrero (2002). Nearrings: Some Developments Linked to Semigroups and Groups. Kluwer Academic Publishers. pp. 62 and 67. ISBN 978-1-4613-0267-4.
- ^ Eric C.R. Hehner (1993). A Practical Theory of Programming. Springer Science & Business Media. p. 230. ISBN 978-1-4419-8596-5.
External links
edit- A demonstration of the Distributive Law for integer arithmetic (from cut-the-knot)








