
Summary
In mathematics, in the theory of functions of several complex variables, a domain of holomorphy is a domain which is maximal in the sense that there exists a holomorphic function on this domain which cannot be extended to a bigger domain.
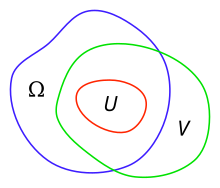
Formally, an open set in the n-dimensional complex space is called a domain of holomorphy if there do not exist non-empty open sets and where is connected, and such that for every holomorphic function on there exists a holomorphic function on with on
In the case, every open set is a domain of holomorphy: we can define a holomorphic function with zeros accumulating everywhere on the boundary of the domain, which must then be a natural boundary for a domain of definition of its reciprocal. For this is no longer true, as it follows from Hartogs' lemma.
Equivalent conditions edit
For a domain the following conditions are equivalent:
- is a domain of holomorphy
- is holomorphically convex
- is pseudoconvex
- is Levi convex - for every sequence of analytic compact surfaces such that for some set we have ( cannot be "touched from inside" by a sequence of analytic surfaces)
- has local Levi property - for every point there exist a neighbourhood of and holomorphic on such that cannot be extended to any neighbourhood of
Implications are standard results (for , see Oka's lemma). The main difficulty lies in proving , i.e. constructing a global holomorphic function which admits no extension from non-extendable functions defined only locally. This is called the Levi problem (after E. E. Levi) and was first solved by Kiyoshi Oka, and then by Lars Hörmander using methods from functional analysis and partial differential equations (a consequence of -problem).
Properties edit
- If are domains of holomorphy, then their intersection is also a domain of holomorphy.
- If is an ascending sequence of domains of holomorphy, then their union is also a domain of holomorphy (see Behnke-Stein theorem).
- If and are domains of holomorphy, then is a domain of holomorphy.
- The first Cousin problem is always solvable in a domain of holomorphy; this is also true, with additional topological assumptions, for the second Cousin problem.
See also edit
- Behnke–Stein theorem
- Levi pseudoconvex
- solution of the Levi problem
- Stein manifold
References edit
- Steven G. Krantz. Function Theory of Several Complex Variables, AMS Chelsea Publishing, Providence, Rhode Island, 1992.
- Boris Vladimirovich Shabat, Introduction to Complex Analysis, AMS, 1992
This article incorporates material from Domain of holomorphy on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.















