
Summary
| Lie groups and Lie algebras |
|---|
 |
In the mathematical field of Lie theory, a Dynkin diagram, named for Eugene Dynkin, is a type of graph with some edges doubled or tripled (drawn as a double or triple line). Dynkin diagrams arise in the classification of semisimple Lie algebras over algebraically closed fields, in the classification of Weyl groups and other finite reflection groups, and in other contexts. Various properties of the Dynkin diagram (such as whether it contains multiple edges, or its symmetries) correspond to important features of the associated Lie algebra.


The term "Dynkin diagram" can be ambiguous. In some cases, Dynkin diagrams are assumed to be directed, in which case they correspond to root systems and semi-simple Lie algebras, while in other cases they are assumed to be undirected, in which case they correspond to Weyl groups. In this article, "Dynkin diagram" means directed Dynkin diagram, and undirected Dynkin diagrams will be explicitly so named.
Classification of semisimple Lie algebras edit
The fundamental interest in Dynkin diagrams is that they classify semisimple Lie algebras over algebraically closed fields. One classifies such Lie algebras via their root system, which can be represented by a Dynkin diagram. One then classifies Dynkin diagrams according to the constraints they must satisfy, as described below.
Dropping the direction on the graph edges corresponds to replacing a root system by the finite reflection group it generates, the so-called Weyl group, and thus undirected Dynkin diagrams classify Weyl groups.
They have the following correspondence for the Lie algebras associated to classical groups over the complex numbers:
- : , the special linear Lie algebra.
- : , the odd-dimensional special orthogonal Lie algebra.
- : , the symplectic Lie algebra.
- : , the even-dimensional special orthogonal Lie algebra ().
For the exceptional groups, the names for the Lie algebra and the associated Dynkin diagram coincide.
Related classifications edit
Dynkin diagrams can be interpreted as classifying many distinct, related objects, and the notation "An, Bn, ..." is used to refer to all such interpretations, depending on context; this ambiguity can be confusing.
The central classification is that a simple Lie algebra has a root system, to which is associated an (oriented) Dynkin diagram; all three of these may be referred to as Bn, for instance.
The unoriented Dynkin diagram is a form of Coxeter diagram, and corresponds to the Weyl group, which is the finite reflection group associated to the root system. Thus Bn may refer to the unoriented diagram (a special kind of Coxeter diagram), the Weyl group (a concrete reflection group), or the abstract Coxeter group.
Although the Weyl group is abstractly isomorphic to the Coxeter group, a specific isomorphism depends on an ordered choice of simple roots. Likewise, while Dynkin diagram notation is standardized, Coxeter diagram and group notation is varied and sometimes agrees with Dynkin diagram notation and sometimes does not.[citation needed]
Lastly, sometimes associated objects are referred to by the same notation, though this cannot always be done regularly. Examples include:
- The root lattice generated by the root system, as in the E8 lattice. This is naturally defined, but not one-to-one – for example, A2 and G2 both generate the hexagonal lattice.
- An associated polytope – for example Gosset 421 polytope may be referred to as "the E8 polytope", as its vertices are derived from the E8 root system and it has the E8 Coxeter group as symmetry group.
- An associated quadratic form or manifold – for example, the E8 manifold has intersection form given by the E8 lattice.
These latter notations are mostly used for objects associated with exceptional diagrams – objects associated to the regular diagrams (A, B, C, D) instead have traditional names.
The index (the n) equals to the number of nodes in the diagram, the number of simple roots in a basis, the dimension of the root lattice and span of the root system, the number of generators of the Coxeter group, and the rank of the Lie algebra. However, n does not equal the dimension of the defining module (a fundamental representation) of the Lie algebra – the index on the Dynkin diagram should not be confused with the index on the Lie algebra. For example, corresponds to which naturally acts on 9-dimensional space, but has rank 4 as a Lie algebra.
The simply laced Dynkin diagrams, those with no multiple edges (A, D, E) classify many further mathematical objects; see discussion at ADE classification.
Example: A2 edit

For example, the symbol may refer to:
- The Dynkin diagram with 2 connected nodes,


 , which may also be interpreted as a Coxeter diagram.
, which may also be interpreted as a Coxeter diagram. - The root system with 2 simple roots at a (120 degree) angle.
- The Lie algebra of rank 2.
- The Weyl group of symmetries of the roots (reflections in the hyperplane orthogonal to the roots), isomorphic to the symmetric group (of order 6).
- The abstract Coxeter group, presented by generators and relations,
Construction from root systems edit
Consider a root system, assumed to be reduced and integral (or "crystallographic"). In many applications, this root system will arise from a semisimple Lie algebra. Let be a set of positive simple roots. We then construct a diagram from as follows.[1] Form a graph with one vertex for each element of . Then insert edges between each pair of vertices according to the following recipe. If the roots corresponding to the two vertices are orthogonal, there is no edge between the vertices. If the angle between the two roots is 120 degrees, we put one edge between the vertices. If the angle is 135 degrees, we put two edges, and if the angle is 150 degrees, we put three edges. (These four cases exhaust all possible angles between pairs of positive simple roots.[2]) Finally, if there are any edges between a given pair of vertices, we decorate them with an arrow pointing from the vertex corresponding to the longer root to the vertex corresponding to the shorter one. (The arrow is omitted if the roots have the same length.) Thinking of the arrow as a "greater than" sign makes it clear which way the arrow should go. Dynkin diagrams lead to a classification of root systems. The angles and length ratios between roots are related.[3] Thus, the edges for non-orthogonal roots may alternatively be described as one edge for a length ratio of 1, two edges for a length ratio of , and three edges for a length ratio of . (There are no edges when the roots are orthogonal, regardless of the length ratio.)
In the root system, shown at right, the roots labeled and form a base. Since these two roots are at angle of 120 degrees (with a length ratio of 1), the Dynkin diagram consists of two vertices connected by a single edge: ![]()
![]()
![]() .
.
Constraints edit
Dynkin diagrams must satisfy certain constraints; these are essentially those satisfied by finite Coxeter–Dynkin diagrams, together with an additional crystallographic constraint.
Connection with Coxeter diagrams edit
Dynkin diagrams are closely related to Coxeter diagrams of finite Coxeter groups, and the terminology is often conflated.[note 1]
Dynkin diagrams differ from Coxeter diagrams of finite groups in two important respects:
- Partly directed
- Dynkin diagrams are partly directed – any multiple edge (in Coxeter terms, labeled with "4" or above) has a direction (an arrow pointing from one node to the other); thus Dynkin diagrams have more data than the underlying Coxeter diagram (undirected graph).
- At the level of root systems the direction corresponds to pointing towards the shorter vector; edges labeled "3" have no direction because the corresponding vectors must have equal length. (Caution: Some authors reverse this convention, with the arrow pointing towards the longer vector.)
- Crystallographic restriction
- Dynkin diagrams must satisfy an additional restriction, namely that the only allowable edge labels are 2, 3, 4, and 6, a restriction not shared by Coxeter diagrams, so not every Coxeter diagram of a finite group comes from a Dynkin diagram.
- At the level of root systems this corresponds to the crystallographic restriction theorem, as the roots form a lattice.
A further difference, which is only stylistic, is that Dynkin diagrams are conventionally drawn with double or triple edges between nodes (for p = 4, 6), rather than an edge labeled with "p".
The term "Dynkin diagram" at times refers to the directed graph, at times to the undirected graph. For precision, in this article "Dynkin diagram" will mean directed, and the underlying undirected graph will be called an "undirected Dynkin diagram". Then Dynkin diagrams and Coxeter diagrams may be related as follows:
| crystallographic | point group | |
|---|---|---|
| directed | Dynkin diagrams | |
| undirected | undirected Dynkin diagrams | Coxeter diagrams of finite groups |
By this is meant that Coxeter diagrams of finite groups correspond to point groups generated by reflections, while Dynkin diagrams must satisfy an additional restriction corresponding to the crystallographic restriction theorem, and that Coxeter diagrams are undirected, while Dynkin diagrams are (partly) directed.
The corresponding mathematical objects classified by the diagrams are:
| crystallographic | point group | |
|---|---|---|
| directed | root systems | |
| undirected | Weyl groups | finite Coxeter groups |
The blank in the upper right, corresponding to directed graphs with underlying undirected graph any Coxeter diagram (of a finite group), can be defined formally, but is little-discussed, and does not appear to admit a simple interpretation in terms of mathematical objects of interest.
There are natural maps down – from Dynkin diagrams to undirected Dynkin diagrams; respectively, from root systems to the associated Weyl groups – and right – from undirected Dynkin diagrams to Coxeter diagrams; respectively from Weyl groups to finite Coxeter groups.
The down map is onto (by definition) but not one-to-one, as the Bn and Cn diagrams map to the same undirected diagram, with the resulting Coxeter diagram and Weyl group thus sometimes denoted BCn.
The right map is simply an inclusion – undirected Dynkin diagrams are special cases of Coxeter diagrams, and Weyl groups are special cases of finite Coxeter groups – and is not onto, as not every Coxeter diagram is an undirected Dynkin diagram (the missed diagrams being H3, H4 and I2(p) for p = 5 p ≥ 7), and correspondingly not every finite Coxeter group is a Weyl group.
Isomorphisms edit

Dynkin diagrams are conventionally numbered so that the list is non-redundant: for for for for and starting at The families can however be defined for lower n, yielding exceptional isomorphisms of diagrams, and corresponding exceptional isomorphisms of Lie algebras and associated Lie groups.
Trivially, one can start the families at or which are all then isomorphic as there is a unique empty diagram and a unique 1-node diagram. The other isomorphisms of connected Dynkin diagrams are:
These isomorphisms correspond to isomorphism of simple and semisimple Lie algebras, which also correspond to certain isomorphisms of Lie group forms of these. They also add context to the En family.[4]
Automorphisms edit

In addition to isomorphism between different diagrams, some diagrams also have self-isomorphisms or "automorphisms". Diagram automorphisms correspond to outer automorphisms of the Lie algebra, meaning that the outer automorphism group Out = Aut/Inn equals the group of diagram automorphisms.[5][6][7]
The diagrams that have non-trivial automorphisms are An (), Dn (), and E6. In all these cases except for D4, there is a single non-trivial automorphism (Out = C2, the cyclic group of order 2), while for D4, the automorphism group is the symmetric group on three letters (S3, order 6) – this phenomenon is known as "triality". It happens that all these diagram automorphisms can be realized as Euclidean symmetries of how the diagrams are conventionally drawn in the plane, but this is just an artifact of how they are drawn, and not intrinsic structure.

For An, the diagram automorphism is reversing the diagram, which is a line. The nodes of the diagram index the fundamental weights, which (for An−1) are for , and the diagram automorphism corresponds to the duality Realized as the Lie algebra the outer automorphism can be expressed as negative transpose, , which is how the dual representation acts.[6]

For Dn, the diagram automorphism is switching the two nodes at the end of the Y, and corresponds to switching the two chiral spin representations. Realized as the Lie algebra the outer automorphism can be expressed as conjugation by a matrix in O(2n) with determinant −1. When n = 3, one has so their automorphisms agree, while is disconnected, and the automorphism corresponds to switching the two nodes.
For D4, the fundamental representation is isomorphic to the two spin representations, and the resulting symmetric group on three letter (S3, or alternatively the dihedral group of order 6, Dih3) corresponds both to automorphisms of the Lie algebra and automorphisms of the diagram.
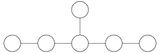
The automorphism group of E6 corresponds to reversing the diagram, and can be expressed using Jordan algebras.[6][8]
Disconnected diagrams, which correspond to semisimple Lie algebras, may have automorphisms from exchanging components of the diagram.

In positive characteristic there are additional "diagram automorphisms" – roughly speaking, in characteristic p one is sometimes allowed to ignore the arrow on bonds of multiplicity p in the Dynkin diagram when taking diagram automorphisms. Thus in characteristic 2 there is an order 2 automorphism of and of F4, while in characteristic 3 there is an order 2 automorphism of G2. But doesn't apply in all circumstances: for example, such automorphisms need not arise as automorphisms of the corresponding algebraic group, but rather on the level of points valued in a finite field.
Construction of Lie groups via diagram automorphisms edit
Diagram automorphisms in turn yield additional Lie groups and groups of Lie type, which are of central importance in the classification of finite simple groups.
The Chevalley group construction of Lie groups in terms of their Dynkin diagram does not yield some of the classical groups, namely the unitary groups and the non-split orthogonal groups. The Steinberg groups construct the unitary groups 2An, while the other orthogonal groups are constructed as 2Dn, where in both cases this refers to combining a diagram automorphism with a field automorphism. This also yields additional exotic Lie groups 2E6 and 3D4, the latter only defined over fields with an order 3 automorphism.
The additional diagram automorphisms in positive characteristic yield the Suzuki–Ree groups, 2B2, 2F4, and 2G2.
Folding edit


A (simply-laced) Dynkin diagram (finite or affine) that has a symmetry (satisfying one condition, below) can be quotiented by the symmetry, yielding a new, generally multiply laced diagram, with the process called folding (due to most symmetries being 2-fold). At the level of Lie algebras, this corresponds to taking the invariant subalgebra under the outer automorphism group, and the process can be defined purely with reference to root systems, without using diagrams.[9] Further, every multiply laced diagram (finite or infinite) can be obtained by folding a simply-laced diagram.[10]
The one condition on the automorphism for folding to be possible is that distinct nodes of the graph in the same orbit (under the automorphism) must not be connected by an edge; at the level of root systems, roots in the same orbit must be orthogonal.[10] At the level of diagrams, this is necessary as otherwise the quotient diagram will have a loop, due to identifying two nodes but having an edge between them, and loops are not allowed in Dynkin diagrams.
The nodes and edges of the quotient ("folded") diagram are the orbits of nodes and edges of the original diagram; the edges are single unless two incident edges map to the same edge (notably at nodes of valence greater than 2) – a "branch point" of the map, in which case the weight is the number of incident edges, and the arrow points towards the node at which they are incident – "the branch point maps to the non-homogeneous point". For example, in D4 folding to G2, the edge in G2 points from the class of the 3 outer nodes (valence 1), to the class of the central node (valence 3).
The foldings of finite diagrams are:[11][note 2]
- (The automorphism of A2n does not yield a folding because the middle two nodes are connected by an edge, but in the same orbit.)
- (if quotienting by the full group or a 3-cycle, in addition to in 3 different ways, if quotienting by an involution)
Similar foldings exist for affine diagrams, including:
The notion of foldings can also be applied more generally to Coxeter diagrams[12] – notably, one can generalize allowable quotients of Dynkin diagrams to Hn and I2(p). Geometrically this corresponds to projections of uniform polytopes. Notably, any simply laced Dynkin diagram can be folded to I2(h), where h is the Coxeter number, which corresponds geometrically to projection to the Coxeter plane.
Folding can be applied to reduce questions about (semisimple) Lie algebras to questions about simply-laced ones, together with an automorphism, which may be simpler than treating multiply laced algebras directly; this can be done in constructing the semisimple Lie algebras, for instance. See Math Overflow: Folding by Automorphisms for further discussion.
Other maps of diagrams edit
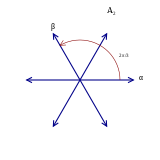 A2 root system |
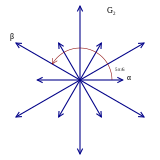 G2 root system |
Some additional maps of diagrams have meaningful interpretations, as detailed below. However, not all maps of root systems arise as maps of diagrams.[13]
For example, there are two inclusions of root systems of A2 in G2, either as the six long roots or the six short roots. However, the nodes in the G2 diagram correspond to one long root and one short root, while the nodes in the A2 diagram correspond to roots of equal length, and thus this map of root systems cannot be expressed as a map of the diagrams.
Some inclusions of root systems can be expressed as one diagram being an induced subgraph of another, meaning "a subset of the nodes, with all edges between them". This is because eliminating a node from a Dynkin diagram corresponds to removing a simple root from a root system, which yields a root system of rank one lower. By contrast, removing an edge (or changing the multiplicity of an edge) while leaving the nodes unchanged corresponds to changing the angles between roots, which cannot be done without changing the entire root system. Thus, one can meaningfully remove nodes, but not edges. Removing a node from a connected diagram may yield a connected diagram (simple Lie algebra), if the node is a leaf, or a disconnected diagram (semisimple but not simple Lie algebra), with either two or three components (the latter for Dn and En). At the level of Lie algebras, these inclusions correspond to sub-Lie algebras.
The maximal subgraphs are as follows; subgraphs related by a diagram automorphism are labeled "conjugate":
- An+1: An, in 2 conjugate ways.
- Bn+1: An, Bn.
- Cn+1: An, Cn.
- Dn+1: An (2 conjugate ways), Dn.
- En+1: An, Dn, En.
- For E6, two of these coincide: and are conjugate.
- F4: B3, C3.
- G2: A1, in 2 non-conjugate ways (as a long root or a short root).
Finally, duality of diagrams corresponds to reversing the direction of arrows, if any:[13] Bn and Cn are dual, while F4, and G2 are self-dual, as are the simply-laced ADE diagrams.
Simply laced edit

A Dynkin diagram with no multiple edges is called simply laced, as are the corresponding Lie algebra and Lie group. These are the diagrams, and phenomena that such diagrams classify are referred to as an ADE classification. In this case the Dynkin diagrams exactly coincide with Coxeter diagrams, as there are no multiple edges.
Satake diagrams edit
Dynkin diagrams classify complex semisimple Lie algebras. Real semisimple Lie algebras can be classified as real forms of complex semisimple Lie algebras, and these are classified by Satake diagrams, which are obtained from the Dynkin diagram by labeling some vertices black (filled), and connecting some other vertices in pairs by arrows, according to certain rules.
History edit

Dynkin diagrams are named for Eugene Dynkin, who used them in two papers (1946, 1947) simplifying the classification of semisimple Lie algebras;[14] see (Dynkin 2000). When Dynkin left the Soviet Union in 1976, which was at the time considered tantamount to treason, Soviet mathematicians were directed to refer to "diagrams of simple roots" rather than use his name.[citation needed]
Undirected graphs had been used earlier by Coxeter (1934) to classify reflection groups, where the nodes corresponded to simple reflections; the graphs were then used (with length information) by Witt (1941) in reference to root systems, with the nodes corresponding to simple roots, as they are used today.[14][15] Dynkin then used them in 1946 and 1947, acknowledging Coxeter and Witt in his 1947 paper.
Conventions edit
Dynkin diagrams have been drawn in a number of ways;[15] the convention followed here is common, with 180° angles on nodes of valence 2, 120° angles on the valence 3 node of Dn, and 90°/90°/180° angles on the valence 3 node of En, with multiplicity indicated by 1, 2, or 3 parallel edges, and root length indicated by drawing an arrow on the edge for orientation. Beyond simplicity, a further benefit of this convention is that diagram automorphisms are realized by Euclidean isometries of the diagrams.
Alternative convention include writing a number by the edge to indicate multiplicity (commonly used in Coxeter diagrams), darkening nodes to indicate root length, or using 120° angles on valence 2 nodes to make the nodes more distinct.
There are also conventions about numbering the nodes. The most common modern convention had developed by the 1960s and is illustrated in (Bourbaki 1968).[15]
Rank 2 Dynkin diagrams edit
Dynkin diagrams are equivalent to generalized Cartan matrices, as shown in this table of rank 2 Dynkin diagrams with their corresponding 2 × 2 Cartan matrices.
For rank 2, the Cartan matrix form is:
A multi-edged diagram corresponds to the nondiagonal Cartan matrix elements , with the number of edges drawn equal to , and an arrow pointing towards nonunity elements.
A generalized Cartan matrix is a square matrix such that:
- For diagonal entries, .
- For non-diagonal entries, .
- if and only if
The Cartan matrix determines whether the group is of finite type (if it is a positive-definite matrix, i.e. all eigenvalues are positive), of affine type (if it is not positive-definite but positive-semidefinite, i.e. all eigenvalues are non-negative), or of indefinite type. The indefinite type often is further subdivided, for example a Coxeter group is Lorentzian if it has one negative eigenvalue and all other eigenvalues are positive. Moreover, multiple sources refer to hyberbolic Coxeter groups, but there are several non-equivalent definitions for this term. In the discussion below, hyperbolic Coxeter groups are a special case of Lorentzian, satisfying an extra condition. For rank 2, all negative determinant Cartan matrices correspond to hyperbolic Coxeter group. But in general, most negative determinant matrices are neither hyperbolic nor Lorentzian.
Finite branches have , and affine branches (with a zero determinant) have .
| Group name |
Dynkin diagram | Cartan matrix | Symmetry order |
Related simply-laced group3 | |||
|---|---|---|---|---|---|---|---|
| (Standard) multi-edged graph |
Valued graph1 |
Coxeter graph2 |
Determinant | ||||
| Finite | Determinant > 0 | ||||||
| A1xA1 | 4 | 2 | |||||
| A2 (undirected) |
3 | 3 | |||||
| B2 | 2 | 4 | | ||||
| C2 | 2 | 4 | | ||||
| BC2 (undirected) |
2 | 4 | |||||
| G2 | 1 | 6 | | ||||
| G2 (undirected) |
1 | 6 | |||||
| Affine | Determinant = 0 | ||||||
| A1(1) | 0 | ∞ | | ||||
| A2(2) | 0 | ∞ | | ||||
| Hyperbolic | Determinant < 0 | ||||||
| −1 | — | ||||||
| −2 | — | ||||||
| −2 | — | ||||||
| −3 | — | ||||||
| −4 | — | ||||||
| −4 | — | ||||||
| −5 | — | ||||||
| — | |||||||
|
Note1: For hyperbolic groups, (a12·a21>4), the multiedge style is abandoned in favor of an explicit labeling (a21, a12) on the edge. These are usually not applied to finite and affine graphs.[16] Note2: For undirected groups, Coxeter diagrams are interchangeable. They are usually labeled by their order of symmetry, with order-3 implied with no label. Note3: Many multi-edged groups can be obtained from a higher ranked simply-laced group by applying a suitable folding operation. | |||||||
Finite Dynkin diagrams edit
| Rank | Classical Lie groups | Exceptional Lie groups | ||||
|---|---|---|---|---|---|---|
| / | ||||||
| 1 | A1 |
|||||
| 2 | A2 |
B2 |
C2=B2 |
D2=A1A1 |
G2 | |
| 3 | A3 |
B3 |
C3 |
D3=A3 |
E3=A2A1 |
|
| 4 | A4 |
B4 |
C4 |
D4 |
E4=A4 |
F4 |
| 5 | A5 |
B5 |
C5 |
D5 |
E5=D5 | |
| 6 | A6 |
B6 |
C6 |
D6 |
E6 | |
| 7 | A7 |
B7 |
C7 |
D7 |
E7 | |
| 8 | A8 |
B8 |
C8 |
D8 |
E8 | |
| 9 | A9 |
B9 |
C9 |
D9 | ||
| 10+ | .. | .. | .. | .. | ||
Affine Dynkin diagrams edit
There are extensions of Dynkin diagrams, namely the affine Dynkin diagrams; these classify Cartan matrices of affine Lie algebras. These are classified in (Kac 1994, Chapter 4, pp. 47–), specifically listed on (Kac 1994, pp. 53–55). Affine diagrams are denoted as or where X is the letter of the corresponding finite diagram, and the exponent depends on which series of affine diagrams they are in. The first of these, are most common, and are called extended Dynkin diagrams and denoted with a tilde, and also sometimes marked with a + superscript.[17] as in . The (2) and (3) series are called twisted affine diagrams.
See Dynkin diagram generator for diagrams.
 The set of extended affine Dynkin diagrams, with added nodes in green ( for and for ) |
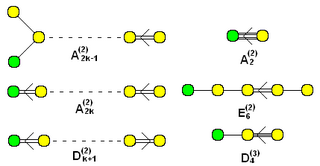 "Twisted" affine forms are named with (2) or (3) superscripts. (The subscript k always counts the number of yellow nodes in the graph, i.e. the total number of nodes minus 1.) |
Here are all of the Dynkin graphs for affine groups up to 10 nodes. Extended Dynkin graphs are given as the ~ families, the same as the finite graphs above, with one node added. Other directed-graph variations are given with a superscript value (2) or (3), representing foldings of higher order groups. These are categorized as Twisted affine diagrams.[18]
| Rank | E / F / G | ||||
|---|---|---|---|---|---|
| 2 | or |
: |
|||
| 3 | or |
or : : |
or | ||
| 4 | or |
or : |
or : : |
||
| 5 | or |
or : |
or : : |
or |
or |
| 6 | or |
or : |
or : : |
or |
|
| 7 | or |
or : |
or : : |
or |
or |
| 8 | or |
or : |
or : : |
or |
or |
| 9 | or |
or : |
or : : |
or |
or |
| 10 | or |
or : |
or : : |
or | |
| 11 | ... | ... | ... | ... |
Hyperbolic and higher Dynkin diagrams edit
The set of compact and noncompact hyperbolic Dynkin graphs has been enumerated.[19] All rank 3 hyperbolic graphs are compact. Compact hyperbolic Dynkin diagrams exist up to rank 5, and noncompact hyperbolic graphs exist up to rank 10.
| Rank | Compact | Noncompact | Total |
|---|---|---|---|
| 3 | 31 | 93 | 123 |
| 4 | 3 | 50 | 53 |
| 5 | 1 | 21 | 22 |
| 6 | 0 | 22 | 22 |
| 7 | 0 | 4 | 4 |
| 8 | 0 | 5 | 5 |
| 9 | 0 | 5 | 5 |
| 10 | 0 | 4 | 4 |
Compact hyperbolic Dynkin diagrams edit
| Rank 3 | Rank 4 | Rank 5 | |
|---|---|---|---|
Linear graphs
|
Cyclic graphs
|
|
|
Noncompact (over-extended) forms edit
Some notations used in theoretical physics, such as M-theory, use a "+" superscript for extended groups instead of a "~" and this allows higher extensions groups to be defined.
- Extended Dynkin diagrams (affine) are given "+" and represent one added node. (Same as "~")
- Over-extended Dynkin diagrams (hyperbolic) are given "^" or "++" and represent two added nodes.
- Very-extended Dynkin diagrams with 3 nodes added are given "+++".
| Rank | AEn = An-2(1)^ | BEn = Bn-2(1)^ CEn |
Cn-2(1)^ | DEn = Dn-2(1)^ | E / F / G |
|---|---|---|---|---|---|
| 3 | AE3: |
||||
| 4 | AE4: |
C2(1)^ A4(2)'^ A4(2)^ D3(2)^ |
G2(1)^ D4(3)^ | ||
| 5 | AE5: |
BE5 CE5 |
C3(1)^ A6(2)^ A6(2)'^ D5(2)^ |
||
| 6 | AE6 |
BE6 CE6 |
C4(1)^ A8(2)^ A8(2)'^ D7(2)^ |
DE6 |
F4(1)^ E6(2)^ |
| 7 | AE7 |
BE7 CE7 |
DE7 |
||
| 8 | AE8 |
BE8 CE8 |
DE8 |
E6(1)^ | |
| 9 | AE9 |
BE9 CE9 |
DE9 |
E7(1)^ | |
| 10 | BE10 CE10 |
DE10 |
E10=E8(1)^ |
238 Hyperbolic groups (compact and noncompact) edit
The 238 hyperbolic groups (compact and noncompact) of rank are named as and listed as for each rank.
Very-extended edit
Very-extended groups are Lorentz groups, defined by adding three nodes to the finite groups. The E8, E7, E6, F4, and G2 offer six series ending as very-extended groups. Other extended series not shown can be defined from An, Bn, Cn, and Dn, as different series for each n. The determinant of the associated Cartan matrix determine where the series changes from finite (positive) to affine (zero) to a noncompact hyperbolic group (negative), and ending as a Lorentz group that can be defined with the use of one time-like dimension, and is used in M theory.[20]
| Finite | |||
|---|---|---|---|
| 2 | A2 |
C2 |
G2 |
| 3 | |||
| 4 | A2++ |
C2++ |
G2++ |
| 5 | A2+++ |
C2+++ |
G2+++ |
| Det(Mn) | 3(3−n) | 2(3−n) | 3−n |
| Finite | |||||||
|---|---|---|---|---|---|---|---|
| 4 | B3A1 |
A3A1 |
A22 | ||||
| 5 | A5 |
D5 |
B4A1 |
D4A1 |
A5 | ||
| 6 | A6 |
B6 |
D6 |
E6 | |||
| 7 | A5++ |
B5++ |
D5++ |
||||
| 8 | A5+++ |
B5+++ |
D5+++ |
A6++ |
B6++ |
D6++ |
E6++ |
| 9 | A6+++ |
B6+++ |
D6+++ |
E6+++ | |||
| Det(Mn) | 6(6−n) | 2(6−n) | 4(6−n) | 7(7−n) | 2(7−n) | 4(7−n) | 3(7−n) |
| Finite | A7 | B7 | D7 | E7 | E8 |
|---|---|---|---|---|---|
| 3 | E3=A2A1 | ||||
| 4 | A3A1 |
E4=A4 | |||
| 5 | A5 |
E5=D5 | |||
| 6 | B5A1 |
D5A1 |
D6 |
E6 | |
| 7 | A7 |
B7 |
D7 |
E7 |
E7 |
| 8 | |
|
|
|
E8 |
| 9 | A7++ |
B7++ |
D7++ |
E7++ |
|
| 10 | A7+++ |
B7+++ |
D7+++ |
E7+++ |
E10=E8++ |
| 11 | E11=E8+++ | ||||
| Det(Mn) | 8(8−n) | 2(8−n) | 4(8−n) | 2(8−n) | 9−n |
See also edit
- Satake diagram
- List of irreducible Tits indices
- Klassifikation von Wurzelsystemen (Classification of root systems) (in German)
Notes edit
Citations edit
- ^ Hall 2015 Section 8.6
- ^ Hall 2015 Propositions 8.6 and 8.13
- ^ Hall 2015 Proposition 8.6
- ^ Baez, John (April 13, 1998), This Week's Finds in Mathematical Physics (Week 119)
- ^ Fulton & Harris 1991, Proposition D.40
- ^ a b c Outer automorphisms of simple Lie Algebras
- ^ Humphreys 1972, § 16.5
- ^ Jacobson 1971, § 7
- ^ Algebraic geometry and number theory: in honor of Vladimir Drinfeld's 50th Birthday, edited by Victor Ginzburg, p. 47, section 3.6: Cluster folding
- ^ a b Folding by Automorphisms Archived 2016-03-04 at the Wayback Machine, John Stembridge, 4pp., 79K, 20 August 2008, Other Articles by John Stembridge
- ^ See Stekolshchik 2008, p. 102, remark 5.4 for illustrations of these foldings and references.
- ^ Zuber, Jean-Bernard (1998). "Generalized Dynkin diagrams and root systems and their folding". In Kashiwara, M.; Matsuo, A.; Saito, K.; Satake, I. (eds.). Topological Field Theory, Primitive Forms and Related Topics. Progress in Mathematics. Vol. 160. pp. 28–30. CiteSeerX 10.1.1.54.3122. doi:10.1007/978-1-4612-0705-4_16. ISBN 978-1-4612-6874-1. S2CID 12429369.
- ^ a b Armstrong, John (March 5, 2010). "Transformations of Dynkin Diagrams".
- ^ a b Knapp 2002, p. 758
- ^ a b c Why are the Dynkin diagrams E6, E7 and E8 always drawn the way they are drawn?
- ^ Section 2.1 in Stekolshchik, Rafael (2005). "Notes on Coxeter Transformations and the McKay correspondence". arXiv:math/0510216v1.
- ^ See for example Humphreys, James E. (1990). "48. Fundamental domain § Affine reflection groups". Reflection Groups and Coxeter Groups. Cambridge University Press. p. 96. ISBN 978-0-521-43613-7.
- ^ Kac, Victor G. (1990). "4. A Classification of Generalized Cartan Matrices". Infinite-Dimensional Lie Algebras. Cambridge University Press. pp. 53–. ISBN 978-0-521-46693-6.
- ^ Carbone, Lisa; Chung, Sjuvon; Cobbs, Leigh; McRae, Robert; Nandi, Debajyoti; Naqvi, Yusra; Penta, Diego (2010). "Classification of hyperbolic Dynkin diagrams, root lengths and Weyl group orbits". Journal of Physics A: Mathematical and Theoretical. 43 (15): 155209. arXiv:1003.0564. Bibcode:2010JPhA...43o5209C. doi:10.1088/1751-8113/43/15/155209. S2CID 16946456.
- ^ Englert, François; Houart, Laurent; Taormina, Anne; West, Peter (2003). "The symmetry of M-theories". Journal of High Energy Physics. 2003 (9): 020. arXiv:hep-th/0304206. Bibcode:2003JHEP...09..020E. doi:10.1088/1126-6708/2003/09/020. S2CID 15680493.
References edit
- Dynkin, E. B. (1947), "The structure of semi-simple algebras .", Uspekhi Mat. Nauk, N.S. (in Russian), 2 (4(20)): 59–127
- Bourbaki, Nicolas (1968), "Chapters 4–6", Groupes et algebres de Lie, Paris: Hermann
- Jacobson, Nathan (1971-06-01), Exceptional Lie Algebras, CRC Press, ISBN 978-0-8247-1326-3
- Humphreys, James E. (1972), Introduction to Lie Algebras and Representation Theory, Birkhäuser, ISBN 978-0-387-90053-7
- Fulton, William; Harris, Joe (1991). Representation theory. A first course. Graduate Texts in Mathematics, Readings in Mathematics. Vol. 129. New York: Springer-Verlag. doi:10.1007/978-1-4612-0979-9. ISBN 978-0-387-97495-8. MR 1153249. OCLC 246650103.
- Dynkin, Evgeniĭ Borisovich; Alexander Adolph Yushkevich; Gary M. Seitz; A. L. Onishchik (2000), Selected papers of E.B. Dynkin with commentary, AMS Bookstore, ISBN 978-0-8218-1065-1
- Hall, Brian C. (2015), Lie Groups, Lie Algebras, and Representations: An Elementary Introduction, Graduate Texts in Mathematics, vol. 222 (2nd ed.), Springer, ISBN 978-3319134666
- Knapp, Anthony W. (2002), Lie groups beyond an introduction (2nd ed.), Birkhäuser, ISBN 978-0-8176-4259-4
- Stekolshchik, R. (2008), Notes on Coxeter Transformations and the McKay Correspondence, Springer Monographs in Mathematics, arXiv:math/0510216, doi:10.1007/978-3-540-77399-3, ISBN 978-3-540-77398-6, S2CID 117958873
- Carbone, Lisa; Chung, Sjuvon; Cobbs, Leigh; Mcrae, Robert; Nandi, Debajyoti; Navqi, Yusra; Penta, Diego (March 2010), "Classification of hyperbolic Dynkin diagrams, root lengths and Weyl group orbits." (PDF), Journal of Physics A: Mathematical and Theoretical, 43 (15): 155209, arXiv:1003.0564, Bibcode:2010JPhA...43o5209C, doi:10.1088/1751-8113/43/15/155209, MR 2608277, S2CID 16946456
- Kac, Victor G. (1994). Infinite-Dimensional Lie Algebras. Cambridge University Press. ISBN 978-0-521-46693-6.
- Dynkin, Eugene B. (2000). Yushkevich, A. A.; Seitz, G. M.; Onishchik, A. L. (eds.). Selected papers of E. B. Dynkin with commentary. Providence, R.I.: American Mathematical Society. ISBN 978-0-8218-1065-1. MR 1757976.
External links edit
- John Baez on the ubiquity of Dynkin diagrams in mathematics
- Web tool for making publication-quality Dynkin diagrams with labels (written in JavaScript)































































![{\displaystyle A=\left[{\begin{matrix}2&a_{12}\\a_{21}&2\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f0c38b6f92dd343e402c1f09e8a077371712646)









![{\displaystyle \left[{\begin{matrix}2&a_{12}\\a_{21}&2\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/609b9b4324da49c4903330c430b14203d6f971cb)

![{\displaystyle \left[{\begin{smallmatrix}2&0\\0&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58d402f7fd38428fe2ac791f5a5d12bf7832c69f)
![{\displaystyle \left[{\begin{smallmatrix}2&-1\\-1&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/18cb26b504d63dba11f3a12c7ee8fa25fe3bdf0a)
![{\displaystyle \left[{\begin{smallmatrix}2&-2\\-1&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07ca67f2863fd2e6f5a6d91133f30d43a1c95805)

![{\displaystyle \left[{\begin{smallmatrix}2&-1\\-2&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a86fb5415f60aea3cee78429d52d340fc1df9ab)
![{\displaystyle \left[{\begin{smallmatrix}2&-{\sqrt {2}}\\-{\sqrt {2}}&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/934421fb85592c1788a92b7d350953dd2ca94b5e)
![{\displaystyle \left[{\begin{smallmatrix}2&-1\\-3&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8008c32cde8626798763d8c84924571bffad4812)

![{\displaystyle \left[{\begin{smallmatrix}2&-{\sqrt {3}}\\-{\sqrt {3}}&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b77e92921199a57f051014d4938de1a0d22ef38)
![{\displaystyle \left[{\begin{smallmatrix}2&-2\\-2&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd86323eaf497d2bb96f757556dd458abd5863cf)

![{\displaystyle \left[{\begin{smallmatrix}2&-1\\-4&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ee764ce2933d720bd85ab4f4425789a0452bb97)

![{\displaystyle \left[{\begin{smallmatrix}2&-1\\-5&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5f8667328ef032fcc28485f9498d0aa472592ef)
![{\displaystyle \left[{\begin{smallmatrix}2&-2\\-3&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de5c1b92cef68df449f22b4667b47f409865b4a9)
![{\displaystyle \left[{\begin{smallmatrix}2&-1\\-6&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/209a341193290b49c172a7b764b7c280f8a4e95e)
![{\displaystyle \left[{\begin{smallmatrix}2&-1\\-7&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13892cd6e699b3c266c6f2c5155a7d3a81171728)
![{\displaystyle \left[{\begin{smallmatrix}2&-2\\-4&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3373a4f62ccb77cbfad04b43f2a9b57dc7fdc618)
![{\displaystyle \left[{\begin{smallmatrix}2&-1\\-8&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/457a113c8f8ee31dbb097965abe5da05593e254b)
![{\displaystyle \left[{\begin{smallmatrix}2&-3\\-3&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58de83867bd03b11edff1e45a0f03073a287b066)
![{\displaystyle \left[{\begin{smallmatrix}2&-b\\-a&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6f2eb2e6d752a7d458a6c9892cee665463ab8fa)


































































































































































