
Summary
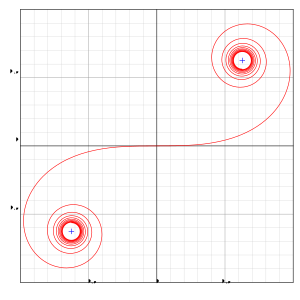
An Euler spiral is a curve whose curvature changes linearly with its curve length (the curvature of a circular curve is equal to the reciprocal of the radius). This curve is also referred to as a clothoid or Cornu spiral.[1][2] The behavior of Fresnel integrals can be illustrated by a Euler spiral, a connection first made by Alfred Marie Cornu 1874.[3] Euler's spiral is a type of superspiral that has the property of a monotonic curvature function.[4]
The Euler spiral has applications to diffraction computations. They are also widely used in railway and highway engineering to design transition curves between straight and curved sections of railway or roads. A similar application is also found in photonic integrated circuits. The principle of linear variation of the curvature of the transition curve between a tangent and a circular curve defines the geometry of the Euler spiral:
- Its curvature begins with zero at the straight section (the tangent) and increases linearly with its curve length.
- Where the Euler spiral meets the circular curve, its curvature becomes equal to that of the latter.
History edit
The spiral has multiple names reflecting its discovery and application in multiple fields. The three major arenas were elastic springs ("Euler spiral", 1744), graphical computations in light diffraction ("Cornu spiral", 1874), and railway transitions ("the railway transition spiral", 1890).[2]
Leonhard Euler's work on the spiral came after James Bernoulli posed a problem in the theory of elasticity: what shape must a pre-curved wire spring be in such that, when flattened by pressing on the free end, it becomes a straight line? Euler established the properties of the spiral in 1744, noting at that time that the curve must have two limits, points that the curve wraps around and around but never reaches. Thirty-eight years later, in 1781, he reported his discovery of the formula for the limit (by "happy chance").[2]
Augustin Fresnel, working in 1818 on the diffraction of light, developed the Fresnel integral that defines the same spiral. He was unaware of Euler's integrals or the connection to the theory of elasticity. In 1874, Alfred Marie Cornu showed that diffraction intensity could be read off of a graph of the spiral by squaring the distance between two points on the graph. In his biographical sketch of Cornu, Henri Poincare praised the advantages of "spiral of Cornu" over the "unpleasant multitude of hairy integral formulas". Ernesto Cesaro chose to name the same curve "clothoid" after Clotho, one of the three Fates who spin the thread of life in Greek mythology.[2]
The third independent discovery occurred in the 1800's when various railway engineers sought a formula for gradual curvature in track shape. By 1880 Arthur Newell Talbot worked out the integral formulas and their solution, which he called the "railway transition spiral". The connection to Euler's work was not made until 1922.[2]
Applications edit
Track transition curve edit
To travel along a circular path, an object needs to be subject to a centripetal acceleration (for example: the Moon circles around the Earth because of gravity; a car turns its front wheels inward to generate a centripetal force). If a vehicle traveling on a straight path were to suddenly transition to a tangential circular path, it would require centripetal acceleration suddenly switching at the tangent point from zero to the required value; this would be difficult to achieve (think of a driver instantly moving the steering wheel from straight line to turning position, and the car actually doing it), putting mechanical stress on the vehicle's parts, and causing much discomfort (due to lateral jerk).
On early railroads this instant application of lateral force was not an issue since low speeds and wide-radius curves were employed (lateral forces on the passengers and the lateral sway was small and tolerable). As speeds of rail vehicles increased over the years, it became obvious that an easement is necessary, so that the centripetal acceleration increases smoothly with the traveled distance. Given the expression of centripetal acceleration v2/r, the obvious solution is to provide an easement curve whose curvature, 1/R, increases linearly with the traveled distance. This geometry is a "clothoid", another name for the Euler spiral.[5]
Unaware of the solution of the geometry by Leonhard Euler, Rankine cited the cubic curve (a polynomial curve of degree 3), which is an approximation of the Euler spiral for small angular changes in the same way that a parabola is an approximation to a circular curve.
Marie Alfred Cornu (and later some civil engineers) also solved the calculus of the Euler spiral independently. Euler spirals are now widely used in rail and highway engineering for providing a transition or an easement between a tangent and a horizontal circular curve.
Optics edit
In optics the term "Cornu spiral" is used.[6]: 432 The Cornu spiral can be used to describe a diffraction pattern.[7] Consider a plane wave with phasor amplitude E0e−jkz which is diffracted by a "knife edge" of height h above x = 0 on the z = 0 plane. Then the diffracted wave field can be expressed as
So, to simplify the calculation of plane wave attenuation as it is diffracted from the knife-edge, one can use the diagram of a Cornu spiral by representing the quantities Fr(a) − Fr(b) as the physical distances between the points represented by Fr(a) and Fr(b) for appropriate a and b. This facilitates a rough computation of the attenuation of the plane wave by the knife edge of height h at a location (x, z) beyond the knife edge.
Integrated optics edit
Bends with continuously varying radius of curvature following the Euler spiral are also used to reduce losses in photonic integrated circuits, either in singlemode waveguides,[8][9] to smoothen the abrupt change of curvature and suppress coupling to radiation modes, or in multimode waveguides,[10] in order to suppress coupling to higher order modes and ensure effective singlemode operation. A pioneering and very elegant application of the Euler spiral to waveguides had been made as early as 1957,[11] with a hollow metal waveguide for microwaves. There the idea was to exploit the fact that a straight metal waveguide can be physically bent to naturally take a gradual bend shape resembling an Euler spiral.
Feynman's path integral edit
In the path integral formulation of quantum mechanics, the probability amplitude for propagation between two points can be visualized by connecting action phase arrows for each time step between the two points. The arrows spiral around each endpoint forming what is termed a Cornu spiral.[12]
Auto racing edit
Motorsport author Adam Brouillard has shown the Euler spiral's use in optimizing the racing line during the corner entry portion of a turn.[13]
Typography and digital vector drawing edit
Raph Levien has released Spiro as a toolkit for curve design, especially font design, in 2007[14][15] under a free licence. This toolkit has been implemented quite quickly afterwards in the font design tool Fontforge and the digital vector drawing Inkscape.
Map projection edit
Cutting a sphere along a spiral with width 1/N and flattening out the resulting shape yields an Euler spiral when n tends to the infinity.[16] If the sphere is the globe, this produces a map projection whose distortion tends to zero as n tends to the infinity.[17]
Whisker shapes edit
Natural shapes of rats' whiskers are well approximated by segments of Euler spirals; for a single rat all of the whiskers can be approximated as segments of the same spiral.[18] The two parameters of the Cesàro equation for an Euler spiral segment might give insight into the keratinization mechanism of whisker growth.[19]
Formulation edit
Symbols edit
| R | Radius of curvature |
| Rc | Radius of circular curve at the end of the spiral |
| θ | Angle of curve from beginning of spiral (infinite R) to a particular point on the spiral.
This can also be measured as the angle between the initial tangent and the tangent at the concerned point. |
| θs | Angle of full spiral curve |
| L, s | Length measured along the spiral curve from its initial position |
| Ls, so | Length of spiral curve |
| Derivation |
|---|
The graph on the right illustrates an Euler spiral used as an easement (transition) curve between two given curves, in this case a straight line (the negative x axis) and a circle. The spiral starts at the origin in the positive x direction and gradually turns anticlockwise to osculate the circle. The spiral is a small segment of the above double-end Euler spiral in the first quadrant. From the definition of the curvature, |
Expansion of Fresnel integral edit
If a = 1, which is the case for normalized Euler curve, then the Cartesian coordinates are given by Fresnel integrals (or Euler integrals):
Normalization edit
For a given Euler curve with:
The process of obtaining solution of (x, y) of an Euler spiral can thus be described as:
- Map L of the original Euler spiral by multiplying with factor a to L′ of the normalized Euler spiral;
- Find (x′, y′) from the Fresnel integrals; and
- Map (x′, y′) to (x, y) by scaling up (denormalize) with factor 1/a. Note that 1/a > 1.
In the normalization process,
Generally the normalization reduces L′ to a small value (less than 1) and results in good converging characteristics of the Fresnel integral manageable with only a few terms (at a price of increased numerical instability of the calculation, especially for bigger θ values.).
Illustration edit
Given:
We scale down the Euler spiral by √60000, i.e. 100√6 to normalized Euler spiral that has:
The two angles θs are the same. This thus confirms that the original and normalized Euler spirals are geometrically similar. The locus of the normalized curve can be determined from Fresnel Integral, while the locus of the original Euler spiral can be obtained by scaling up or denormalizing.
Other properties of normalized Euler spirals edit
Normalized Euler spirals can be expressed as:
The normalized Euler spiral will converge to a single point in the limit as the parameter L approaches infinity, which can be expressed as:
Normalized Euler spirals have the following properties:
Note that 2RcLs = 1 also means 1/Rc = 2Ls, in agreement with the last mathematical statement.
See also edit
References edit
- ^ Von Seggern, David H. (1994). Practical handbook of curve design and generation. Boca Raton, Fla.: CRC Press. ISBN 978-0-8493-8916-0.
- ^ a b c d e Levien, Raph. "The Euler spiral: a mathematical history." Rapp. tech (2008).
- ^ Marie Alfred Cornu. M´ethode nouvelle pour la discussion des probl´emes de diffraction dans le cas d’une onde cylindrique. Journal de Physique th´eoretique et appliqu´ee, pages 5–15, 1874.
- ^ Ziatdinov, R. (2012), "Family of superspirals with completely monotonic curvature given in terms of Gauss hypergeometric function", Computer Aided Geometric Design, 29 (7): 510–518
- ^ Constantin (2016-03-07). "The Clothoid". Pwayblog. Retrieved 2023-06-07.
- ^ Born, Max; Wolf, Emil (1993). Principles of optics: electromagnetic theory of propagation, interference and diffraction of light (6. ed., reprinted (with corrections) ed.). Oxford: Pergamon Press. ISBN 978-0-08-026481-3.
- ^ Eugene Hecht (1998). Optics (3rd ed.). Addison-Wesley. p. 491. ISBN 978-0-201-30425-1.
- ^ Kohtoku, M.; et al. (7 July 2005). "New Waveguide Fabrication Techniques for Next-generation PLCs" (PDF). NTT Technical Review. 3 (7): 37–41. Retrieved 24 January 2017.
- ^ Li, G.; et al. (11 May 2012). "Ultralow-loss, high-density SOI optical waveguide routing for macrochip interconnects". Optics Express. 20 (11): 12035–12039. Bibcode:2012OExpr..2012035L. doi:10.1364/OE.20.012035. PMID 22714189.
- ^ Cherchi, M.; et al. (18 July 2013). "Dramatic size reduction of waveguide bends on a micron-scale silicon photonic platform". Optics Express. 21 (15): 17814–17823. arXiv:1301.2197. Bibcode:2013OExpr..2117814C. doi:10.1364/OE.21.017814. PMID 23938654.
- ^ Unger, H.G. (September 1957). "Normal Mode Bends for Circular Electric Waves". The Bell System Technical Journal. 36 (5): 1292–1307. doi:10.1002/j.1538-7305.1957.tb01509.x.
- ^ Taylor, Edwin F.; Vokos, Stamatis; O’Meara, John M.; Thornber, Nora S. (1998-03-01). "Teaching Feynman's sum-over-paths quantum theory". Computers in Physics. 12 (2): 190–199. doi:10.1063/1.168652. ISSN 0894-1866.
- ^ Development, Paradigm Shift Driver; Brouillard, Adam (2016-03-18). The Perfect Corner: A Driver's Step-By-Step Guide to Finding Their Own Optimal Line Through the Physics of Racing. Paradigm Shift Motorsport Books. ISBN 9780997382426.
- ^ "Spiro".
- ^ "| Spiro 0.01 release | Typophile". www.typophile.com. Archived from the original on 2007-05-10.
- ^ Bartholdi, Laurent; Henriques, André (2012). "Orange Peels and Fresnel Integrals". The Mathematical Intelligencer. 34 (3): 1–3. arXiv:1202.3033. doi:10.1007/s00283-012-9304-1. ISSN 0343-6993. S2CID 52592272.
- ^ "A Strange Map Projection (Euler Spiral) - Numberphile". YouTube. Archived from the original on 2021-12-21.
- ^ Towal, R.B.; et al. (7 April 2011). "The Morphology of the Rat Vibrissal Array: A Model for Quantifying Spatiotemporal Patterns of Whisker-Object Contact". PLoS Computational Biology. 7 (4): e1001120. doi:10.1371/journal.pcbi.1001120. PMC 3072363. PMID 21490724. Starostin, E.L.; et al. (15 January 2020). "The Euler spiral of rat whiskers". Science Advances. 6 (3): eaax5145. Bibcode:2020SciA....6.5145S. doi:10.1126/sciadv.aax5145. PMC 6962041. PMID 31998835.
- ^ Luo, Y.; Hartmann, M.J. (Jan 2023). "On the intrinsic curvature of animal whiskers". PLoS One. 18 (1): e0269210. doi:10.1371/journal.pone.0269210. PMC 9821693. PMID 36607960.
Further reading edit
- Kellogg, Norman Benjamin (1907). The Transition Curve or Curve of Adjustment (3rd ed.). New York: McGraw.
- R. Nave, The Cornu spiral, Hyperphysics (2002) (Uses πt²/2 instead of t².)
- Milton Abramowitz and Irene A. Stegun, eds. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover, 1972. (See Chapter 7)
- "Roller Coaster Loop Shapes". Retrieved 2010-11-12.
External links edit
- Weisstein, Eric W. "Cornu Spiral". MathWorld.
- Euler's spiral at 2-D Mathematical Curves
- Interactive example with JSXGraph


