
Summary
In physics, Hooke's law is an empirical law which states that the force (F) needed to extend or compress a spring by some distance (x) scales linearly with respect to that distance—that is, Fs = kx, where k is a constant factor characteristic of the spring (i.e., its stiffness), and x is small compared to the total possible deformation of the spring. The law is named after 17th-century British physicist Robert Hooke. He first stated the law in 1676 as a Latin anagram.[1][2] He published the solution of his anagram in 1678[3] as: ut tensio, sic vis ("as the extension, so the force" or "the extension is proportional to the force"). Hooke states in the 1678 work that he was aware of the law since 1660.
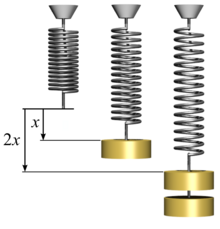


Hooke's equation holds (to some extent) in many other situations where an elastic body is deformed, such as wind blowing on a tall building, and a musician plucking a string of a guitar. An elastic body or material for which this equation can be assumed is said to be linear-elastic or Hookean.
Hooke's law is only a first-order linear approximation to the real response of springs and other elastic bodies to applied forces. It must eventually fail once the forces exceed some limit, since no material can be compressed beyond a certain minimum size, or stretched beyond a maximum size, without some permanent deformation or change of state. Many materials will noticeably deviate from Hooke's law well before those elastic limits are reached.
On the other hand, Hooke's law is an accurate approximation for most solid bodies, as long as the forces and deformations are small enough. For this reason, Hooke's law is extensively used in all branches of science and engineering, and is the foundation of many disciplines such as seismology, molecular mechanics and acoustics. It is also the fundamental principle behind the spring scale, the manometer, the galvanometer, and the balance wheel of the mechanical clock.
The modern theory of elasticity generalizes Hooke's law to say that the strain (deformation) of an elastic object or material is proportional to the stress applied to it. However, since general stresses and strains may have multiple independent components, the "proportionality factor" may no longer be just a single real number, but rather a linear map (a tensor) that can be represented by a matrix of real numbers.
In this general form, Hooke's law makes it possible to deduce the relation between strain and stress for complex objects in terms of intrinsic properties of the materials they are made of. For example, one can deduce that a homogeneous rod with uniform cross section will behave like a simple spring when stretched, with a stiffness k directly proportional to its cross-section area and inversely proportional to its length.
Formal definition edit
Linear springs edit
Consider a simple helical spring that has one end attached to some fixed object, while the free end is being pulled by a force whose magnitude is Fs. Suppose that the spring has reached a state of equilibrium, where its length is not changing anymore. Let x be the amount by which the free end of the spring was displaced from its "relaxed" position (when it is not being stretched). Hooke's law states that
According to this formula, the graph of the applied force Fs as a function of the displacement x will be a straight line passing through the origin, whose slope is k.
Hooke's law for a spring is also stated under the convention that Fs is the restoring force exerted by the spring on whatever is pulling its free end. In that case, the equation becomes
Torsional springs edit
The torsional analog of Hooke's law applies to torsional springs. It states that the torque (τ) required to rotate an object is directly proportional to the angular displacement (θ) from the equilibrium position. It describes the relationship between the torque applied to an object and the resulting angular deformation due to torsion. Mathematically, it can be expressed as:
Where:
- τ is the torque measured in Newton-meters or N·m.
- k is the torsional constant (measured in N·m/radian), which characterizes the stiffness of the torsional spring or the resistance to angular displacement.
- θ is the angular displacement (measured in radians) from the equilibrium position.
Just as in the linear case, this law shows that the torque is proportional to the angular displacement, and the negative sign indicates that the torque acts in a direction opposite to the angular displacement, providing a restoring force to bring the system back to equilibrium.
General "scalar" springs edit
Hooke's spring law usually applies to any elastic object, of arbitrary complexity, as long as both the deformation and the stress can be expressed by a single number that can be both positive and negative.
For example, when a block of rubber attached to two parallel plates is deformed by shearing, rather than stretching or compression, the shearing force Fs and the sideways displacement of the plates x obey Hooke's law (for small enough deformations).
Hooke's law also applies when a straight steel bar or concrete beam (like the one used in buildings), supported at both ends, is bent by a weight F placed at some intermediate point. The displacement x in this case is the deviation of the beam, measured in the transversal direction, relative to its unloaded shape.
Vector formulation edit
In the case of a helical spring that is stretched or compressed along its axis, the applied (or restoring) force and the resulting elongation or compression have the same direction (which is the direction of said axis). Therefore, if Fs and x are defined as vectors, Hooke's equation still holds and says that the force vector is the elongation vector multiplied by a fixed scalar.
General tensor form edit
Some elastic bodies will deform in one direction when subjected to a force with a different direction. One example is a horizontal wood beam with non-square rectangular cross section that is bent by a transverse load that is neither vertical nor horizontal. In such cases, the magnitude of the displacement x will be proportional to the magnitude of the force Fs, as long as the direction of the latter remains the same (and its value is not too large); so the scalar version of Hooke's law Fs = −kx will hold. However, the force and displacement vectors will not be scalar multiples of each other, since they have different directions. Moreover, the ratio k between their magnitudes will depend on the direction of the vector Fs.
Yet, in such cases there is often a fixed linear relation between the force and deformation vectors, as long as they are small enough. Namely, there is a function κ from vectors to vectors, such that F = κ(X), and κ(αX1 + βX2) = ακ(X1) + βκ(X2) for any real numbers α, β and any displacement vectors X1, X2. Such a function is called a (second-order) tensor.
With respect to an arbitrary Cartesian coordinate system, the force and displacement vectors can be represented by 3 × 1 matrices of real numbers. Then the tensor κ connecting them can be represented by a 3 × 3 matrix κ of real coefficients, that, when multiplied by the displacement vector, gives the force vector:
Hooke's law for continuous media edit
The stresses and strains of the material inside a continuous elastic material (such as a block of rubber, the wall of a boiler, or a steel bar) are connected by a linear relationship that is mathematically similar to Hooke's spring law, and is often referred to by that name.
However, the strain state in a solid medium around some point cannot be described by a single vector. The same parcel of material, no matter how small, can be compressed, stretched, and sheared at the same time, along different directions. Likewise, the stresses in that parcel can be at once pushing, pulling, and shearing.
In order to capture this complexity, the relevant state of the medium around a point must be represented by two-second-order tensors, the strain tensor ε (in lieu of the displacement X) and the stress tensor σ (replacing the restoring force F). The analogue of Hooke's spring law for continuous media is then
In a Cartesian coordinate system, the stress and strain tensors can be represented by 3 × 3 matrices
All three tensors generally vary from point to point inside the medium, and may vary with time as well. The strain tensor ε merely specifies the displacement of the medium particles in the neighborhood of the point, while the stress tensor σ specifies the forces that neighboring parcels of the medium are exerting on each other. Therefore, they are independent of the composition and physical state of the material. The stiffness tensor c, on the other hand, is a property of the material, and often depends on physical state variables such as temperature, pressure, and microstructure.
Due to the inherent symmetries of σ, ε, and c, only 21 elastic coefficients of the latter are independent.[6] This number can be further reduced by the symmetry of the material: 9 for an orthorhombic crystal, 5 for an hexagonal structure, and 3 for a cubic symmetry.[7] For isotropic media (which have the same physical properties in any direction), c can be reduced to only two independent numbers, the bulk modulus K and the shear modulus G, that quantify the material's resistance to changes in volume and to shearing deformations, respectively.
Analogous laws edit
Since Hooke's law is a simple proportionality between two quantities, its formulas and consequences are mathematically similar to those of many other physical laws, such as those describing the motion of fluids, or the polarization of a dielectric by an electric field.
In particular, the tensor equation σ = cε relating elastic stresses to strains is entirely similar to the equation τ = με̇ relating the viscous stress tensor τ and the strain rate tensor ε̇ in flows of viscous fluids; although the former pertains to static stresses (related to amount of deformation) while the latter pertains to dynamical stresses (related to the rate of deformation).
Units of measurement edit
In SI units, displacements are measured in meters (m), and forces in newtons (N or kg·m/s2). Therefore, the spring constant k, and each element of the tensor κ, is measured in newtons per meter (N/m), or kilograms per second squared (kg/s2).
For continuous media, each element of the stress tensor σ is a force divided by an area; it is therefore measured in units of pressure, namely pascals (Pa, or N/m2, or kg/(m·s2). The elements of the strain tensor ε are dimensionless (displacements divided by distances). Therefore, the entries of cijkl are also expressed in units of pressure.
General application to elastic materials edit
- Ultimate strength
- Yield strength (yield point)
- Rupture
- Strain hardening region
- Necking region
- Apparent stress (F/A0)
- Actual stress (F/A)
Objects that quickly regain their original shape after being deformed by a force, with the molecules or atoms of their material returning to the initial state of stable equilibrium, often obey Hooke's law.
Hooke's law only holds for some materials under certain loading conditions. Steel exhibits linear-elastic behavior in most engineering applications; Hooke's law is valid for it throughout its elastic range (i.e., for stresses below the yield strength). For some other materials, such as aluminium, Hooke's law is only valid for a portion of the elastic range. For these materials a proportional limit stress is defined, below which the errors associated with the linear approximation are negligible.
Rubber is generally regarded as a "non-Hookean" material because its elasticity is stress dependent and sensitive to temperature and loading rate.
Generalizations of Hooke's law for the case of large deformations is provided by models of neo-Hookean solids and Mooney–Rivlin solids.
Derived formulae edit
Tensional stress of a uniform bar edit
A rod of any elastic material may be viewed as a linear spring. The rod has length L and cross-sectional area A. Its tensile stress σ is linearly proportional to its fractional extension or strain ε by the modulus of elasticity E:
The modulus of elasticity may often be considered constant. In turn,
The change in length may be expressed as
Spring energy edit
The potential energy Uel(x) stored in a spring is given by
This potential Uel can be visualized as a parabola on the Ux-plane such that Uel(x) = 1/2kx2. As the spring is stretched in the positive x-direction, the potential energy increases parabolically (the same thing happens as the spring is compressed). Since the change in potential energy changes at a constant rate:
Relaxed force constants (generalized compliance constants) edit
Relaxed force constants (the inverse of generalized compliance constants) are uniquely defined for molecular systems, in contradistinction to the usual "rigid" force constants, and thus their use allows meaningful correlations to be made between force fields calculated for reactants, transition states, and products of a chemical reaction. Just as the potential energy can be written as a quadratic form in the internal coordinates, so it can also be written in terms of generalized forces. The resulting coefficients are termed compliance constants. A direct method exists for calculating the compliance constant for any internal coordinate of a molecule, without the need to do the normal mode analysis.[8] The suitability of relaxed force constants (inverse compliance constants) as covalent bond strength descriptors was demonstrated as early as 1980. Recently, the suitability as non-covalent bond strength descriptors was demonstrated too.[9]
Harmonic oscillator edit
A mass m attached to the end of a spring is a classic example of a harmonic oscillator. By pulling slightly on the mass and then releasing it, the system will be set in sinusoidal oscillating motion about the equilibrium position. To the extent that the spring obeys Hooke's law, and that one can neglect friction and the mass of the spring, the amplitude of the oscillation will remain constant; and its frequency f will be independent of its amplitude, determined only by the mass and the stiffness of the spring:
Rotation in gravity-free space edit
If the mass m were attached to a spring with force constant k and rotating in free space, the spring tension (Ft) would supply the required centripetal force (Fc):
Linear elasticity theory for continuous media edit
Isotropic materials edit
Isotropic materials are characterized by properties which are independent of direction in space. Physical equations involving isotropic materials must therefore be independent of the coordinate system chosen to represent them. The strain tensor is a symmetric tensor. Since the trace of any tensor is independent of any coordinate system, the most complete coordinate-free decomposition of a symmetric tensor is to represent it as the sum of a constant tensor and a traceless symmetric tensor.[10] Thus in index notation:
The first term on the right is the constant tensor, also known as the volumetric strain tensor, and the second term is the traceless symmetric tensor, also known as the deviatoric strain tensor or shear tensor.
The most general form of Hooke's law for isotropic materials may now be written as a linear combination of these two tensors:
Using the relationships between the elastic moduli, these equations may also be expressed in various other ways. A common form of Hooke's law for isotropic materials, expressed in direct tensor notation, is [11] where λ = K − 2/3G = c1111 − 2c1212 and μ = G = c1212 are the Lamé constants, I is the second-rank identity tensor, and I is the symmetric part of the fourth-rank identity tensor. In index notation:
The three-dimensional form of Hooke's law can be derived using Poisson's ratio and the one-dimensional form of Hooke's law as follows. Consider the strain and stress relation as a superposition of two effects: stretching in direction of the load (1) and shrinking (caused by the load) in perpendicular directions (2 and 3),
We get similar equations to the loads in directions 2 and 3,
Summing the three cases together (εi = εi′ + εi″ + εi‴) we get
Calculating the sum
Similar treatment of directions 2 and 3 gives the Hooke's law in three dimensions.
In matrix form, Hooke's law for isotropic materials can be written as
Plane stress edit
Under plane stress conditions, σ31 = σ13 = σ32 = σ23 = σ33 = 0. In that case Hooke's law takes the form
In vector notation this becomes
The inverse relation is usually written in the reduced form
Plane strain edit
Under plane strain conditions, ε31 = ε13 = ε32 = ε23 = ε33 = 0. In this case Hooke's law takes the form
Anisotropic materials edit
The symmetry of the Cauchy stress tensor (σij = σji) and the generalized Hooke's laws (σij = cijklεkl) implies that cijkl = cjikl. Similarly, the symmetry of the infinitesimal strain tensor implies that cijkl = cijlk. These symmetries are called the minor symmetries of the stiffness tensor c. This reduces the number of elastic constants from 81 to 36.
If in addition, since the displacement gradient and the Cauchy stress are work conjugate, the stress–strain relation can be derived from a strain energy density functional (U), then
Matrix representation (stiffness tensor) edit
It is often useful to express the anisotropic form of Hooke's law in matrix notation, also called Voigt notation. To do this we take advantage of the symmetry of the stress and strain tensors and express them as six-dimensional vectors in an orthonormal coordinate system (e1,e2,e3) as
Change of coordinate system edit
If a linear elastic material is rotated from a reference configuration to another, then the material is symmetric with respect to the rotation if the components of the stiffness tensor in the rotated configuration are related to the components in the reference configuration by the relation[13]
In matrix notation, if the transformed basis (rotated or inverted) is related to the reference basis by
Orthotropic materials edit
Orthotropic materials have three orthogonal planes of symmetry. If the basis vectors (e1,e2,e3) are normals to the planes of symmetry then the coordinate transformation relations imply that
- Ei is the Young's modulus along axis i
- Gij is the shear modulus in direction j on the plane whose normal is in direction i
- νij is the Poisson's ratio that corresponds to a contraction in direction j when an extension is applied in direction i.
Under plane stress conditions, σzz = σzx = σyz = 0, Hooke's law for an orthotropic material takes the form
Transversely isotropic materials edit
A transversely isotropic material is symmetric with respect to a rotation about an axis of symmetry. For such a material, if e3 is the axis of symmetry, Hooke's law can be expressed as
More frequently, the x ≡ e1 axis is taken to be the axis of symmetry and the inverse Hooke's law is written as [15]
Universal elastic anisotropy index edit
To grasp the degree of anisotropy of any class, a universal elastic anisotropy index (AU)[16] was formulated. It replaces the Zener ratio, which is suited for cubic crystals.
Thermodynamic basis edit
Linear deformations of elastic materials can be approximated as adiabatic. Under these conditions and for quasistatic processes the first law of thermodynamics for a deformed body can be expressed as
See also edit
Notes edit
- ^ The anagram was given in alphabetical order, ceiiinosssttuu, representing Ut tensio, sic vis – "As the extension, so the force": Petroski, Henry (1996). Invention by Design: How Engineers Get from Thought to Thing. Cambridge, MA: Harvard University Press. p. 11. ISBN 978-0674463684.
- ^ See http://civil.lindahall.org/design.shtml, where one can find also an anagram for catenary.
- ^ Robert Hooke, De Potentia Restitutiva, or of Spring. Explaining the Power of Springing Bodies, London, 1678.
- ^ Young, Hugh D.; Freedman, Roger A.; Ford, A. Lewis (2016). Sears and Zemansky's University Physics: With Modern Physics (14th ed.). Pearson. p. 209.
- ^ Ushiba, Shota; Masui, Kyoko; Taguchi, Natsuo; Hamano, Tomoki; Kawata, Satoshi; Shoji, Satoru (2015). "Size dependent nanomechanics of coil spring shaped polymer nanowires". Scientific Reports. 5: 17152. Bibcode:2015NatSR...517152U. doi:10.1038/srep17152. PMC 4661696. PMID 26612544.
- ^ Belen'kii; Salaev (1988). "Deformation effects in layer crystals". Uspekhi Fizicheskikh Nauk. 155 (5): 89. doi:10.3367/UFNr.0155.198805c.0089.
- ^ Mouhat, Félix; Coudert, François-Xavier (5 December 2014). "Necessary and sufficient elastic stability conditions in various crystal systems". Physical Review B. 90 (22): 224104. arXiv:1410.0065. Bibcode:2014PhRvB..90v4104M. doi:10.1103/PhysRevB.90.224104. ISSN 1098-0121. S2CID 54058316.
- ^ Vijay Madhav, M.; Manogaran, S. (2009). "A relook at the compliance constants in redundant internal coordinates and some new insights". J. Chem. Phys. 131 (17): 174112–174116. Bibcode:2009JChPh.131q4112V. doi:10.1063/1.3259834. PMID 19895003.
- ^ Ponomareva, Alla; Yurenko, Yevgen; Zhurakivsky, Roman; Van Mourik, Tanja; Hovorun, Dmytro (2012). "Complete conformational space of the potential HIV-1 reverse transcriptase inhibitors d4U and d4C. A quantum chemical study". Phys. Chem. Chem. Phys. 14 (19): 6787–6795. Bibcode:2012PCCP...14.6787P. doi:10.1039/C2CP40290D. PMID 22461011.
- ^ Symon, Keith R. (1971). "Chapter 10". Mechanics. Reading, Massachusetts: Addison-Wesley. ISBN 9780201073928.
- ^ Simo, J. C.; Hughes, T. J. R. (1998). Computational Inelasticity. Springer. ISBN 9780387975207.
- ^ Milton, Graeme W. (2002). The Theory of Composites. Cambridge Monographs on Applied and Computational Mathematics. Cambridge University Press. ISBN 9780521781251.
- ^ Slaughter, William S. (2001). The Linearized Theory of Elasticity. Birkhäuser. ISBN 978-0817641177.
- ^ Boresi, A. P.; Schmidt, R. J.; Sidebottom, O. M. (1993). Advanced Mechanics of Materials (5th ed.). Wiley. ISBN 9780471600091.
- ^ Tan, S. C. (1994). Stress Concentrations in Laminated Composites. Lancaster, PA: Technomic Publishing Company. ISBN 9781566760775.
- ^ Ranganathan, S.I.; Ostoja-Starzewski, M. (2008). "Universal Elastic Anisotropy Index". Physical Review Letters. 101 (5): 055504–1–4. Bibcode:2008PhRvL.101e5504R. doi:10.1103/PhysRevLett.101.055504. PMID 18764407. S2CID 6668703.
References edit
- Hooke's law - The Feynman Lectures on Physics
- Hooke's Law - Classical Mechanics - Physics - MIT OpenCourseWare
External links edit
- JavaScript Applet demonstrating Springs and Hooke's law
- JavaScript Applet demonstrating Spring Force
| Conversion formulae | |||||||
|---|---|---|---|---|---|---|---|
| Homogeneous isotropic linear elastic materials have their elastic properties uniquely determined by any two moduli among these; thus, given any two, any other of the elastic moduli can be calculated according to these formulas, provided both for 3D materials (first part of the table) and for 2D materials (second part). | |||||||
| 3D formulae | Notes | ||||||
| There are two valid solutions. | |||||||
| Cannot be used when | |||||||
| 2D formulae | Notes | ||||||
| Cannot be used when | |||||||
|
| |||||||


