
Summary
An impact structure is a generally circular or craterlike geologic structure of deformed bedrock or sediment produced by impact on a planetary surface, whatever the stage of erosion of the structure. In contrast, an impact crater is the surface expression of an impact structure. In many cases, on Earth, the impact crater has been destroyed by erosion, leaving only the deformed rock or sediment of the impact structure behind.[1] This is the fate of almost all old impact craters on Earth, unlike the ancient pristine craters preserved on the Moon and other geologically inactive rocky bodies with old surfaces[2] in the Solar System. Impact structure is synonymous with the less commonly used term astrobleme meaning "star wound".[3]
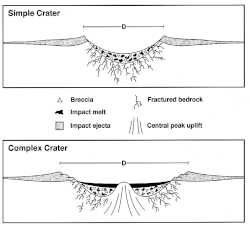
In an impact structure, the typical visible and topographic expressions of an impact crater are no longer obvious. Any meteorite fragments that may once have been present would be long since eroded away. Possible impact structures may be initially recognized by their anomalous geological character or geophysical expression. These may still be confirmed as impact structures by the presence of shocked minerals (particularly shocked quartz), shatter cones, geochemical evidence of extraterrestrial material or other methods.
See also edit
- Complex crater
- Earth Impact Database
- Multi-ringed basin
- Impact event
- List of impact craters on Earth
- List of possible impact structures on Earth
- Traces of Catastrophe book from Lunar and Planetary Institute - comprehensive reference on impact crater science
- Peak ring
References edit
- ^ Neuendorf, K.K.E., J.P. Mehl Jr., and J.A. Jackson, eds. (2005) Glossary of Geology (5th ed.). Alexandria, Virginia, American Geological Institute. 779 pp. ISBN 0-922152-76-4
- ^ Moore, Jeffrey M.; Black, Greg; Buratti, Bonnie; Phillips, Cynthia B.; Spencer, John; Sullivan, Robert (2009). "Surface Properties, Regolith, and Landscape Degradation". In Pappalardo, Robert T. (ed.). Europa. The University of Arizona space science series. McKinnon, William B.; Khurana, Krishan. Tucson: The University of Arizona Press. p. 341. ISBN 978-0-8165-2844-8.
Bodies with current geological activity such as Io and Earth have very few recognizable impact craters—Io, in fact, is so volcanically active that not a single impact crater, of any size, has been found on its surface to date. The Earth has about 150 recognized craters, but many have been geologically modified and would be difficult to recognize from orbit. On the other hand, geologically inactive bodies with old surfaces, such as Earth's Moon or Callisto, are covered with impact craters of all sizes.
- ^ French, Bevan M (1998). Traces of Catastrophe: A Handbook of Shock-Metamorphic Effects in Terrestrial Meteorite Impact Structures. Houston, Texas: Lunar and Planetary Institute. p. 120. LPI Contribution No. 954.
External links edit
- Terrestrial Impact Craters at the Lunar and Planetary Institute
- Earth Impact Database


