
Summary
Kleiber's law, named after Max Kleiber for his biology work in the early 1930s, is the observation that, for the vast majority of animals, an animal's metabolic rate scales to the 3⁄4 power of the animal's mass.[2] More recently, Kleiber's law has also been shown to apply in plants,[3] suggesting that Kleiber's observation is much more general. Symbolically: if B is the animal's metabolic rate, and M is the animal's mass, then Kleiber's law states that B~M3/4. Thus, over the same time span, a cat having a mass 100 times that of a mouse will consume only about 32 times the energy the mouse uses.
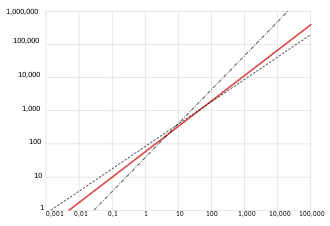
The exact value of the exponent in Kleiber's law is unclear, in part because the law currently lacks a single theoretical explanation that is entirely satisfactory.
Proposed explanations for the law edit
Kleiber's law, like many other biological allometric laws, is a consequence of the physics and/or geometry of circulatory systems in biology.[4] Max Kleiber first discovered the law when analyzing a large number of independent studies on respiration within individual species.[2] Kleiber expected to find an exponent of 2⁄3 (for reasons explained below), and was confounded by the discovery of a 3⁄4 exponent.
Historical context and the 2⁄3 scaling surface law edit
Before Kleiber's observation of the 3/4 power scaling, a 2/3 power scaling was largely anticipated based on the "surface law",[5] which states that the basal metabolism of animals differing in size is nearly proportional to their respective body surfaces. This surface law reasoning originated from simple geometrical considerations. As organisms increase in size, their volume (and thus mass) increases at a much faster rate than their surface area. Explanations for 2⁄3-scaling tend to assume that metabolic rates scale to avoid heat exhaustion. Because bodies lose heat passively via their surface but produce heat metabolically throughout their mass, the metabolic rate must scale in such a way as to counteract the square–cube law. Because many physiological processes, like heat loss and nutrient uptake, were believed to be dependent on the surface area of an organism, it was hypothesized that metabolic rate would scale with the 2/3 power of body mass.[6] Rubner (1883) first demonstrated the law in accurate respiration trials on dogs.[7]
Kleiber's contribution edit
Max Kleiber challenged this notion in the early 1930s. Through extensive research on various animals' metabolic rates, he found that a 3/4 power scaling provided a better fit to the empirical data than the 2/3 power.[2] His findings provided the groundwork for understanding allometric scaling laws in biology, leading to the formulation of the Metabolic Scaling Theory and the later work by West, Brown, and Enquist, among others.
Such an argument does not address the fact that different organisms exhibit different shapes (and hence have different surface-area-to-volume ratios, even when scaled to the same size). Reasonable estimates for organisms' surface area do appear to scale linearly with the metabolic rate.[8]
Exponent 3⁄4 edit
West, Brown, and Enquist, (hereafter WBE) proposed a general theory for the origin of many allometric scaling laws in biology. According to the WBE theory, 3⁄4-scaling arises because of efficiency in nutrient distribution and transport throughout an organism. In most organisms, metabolism is supported by a circulatory system featuring branching tubules (i.e., plant vascular systems, insect tracheae, or the human cardiovascular system). WEB claim that (1) metabolism should scale proportionally to nutrient flow (or, equivalently, total fluid flow) in this circulatory system and (2) in order to minimize the energy dissipated in transport, the volume of fluid used to transport nutrients (i.e., blood volume) is a fixed fraction of body mass.[9]
They then analyze the consequences of these two claims at the level of the smallest circulatory tubules (capillaries, alveoli, etc.). Experimentally, the volume contained in those smallest tubules is constant across a wide range of masses. Because fluid flow through a tubule is determined by the volume thereof, the total fluid flow is proportional to the total number of smallest tubules. Thus, if B denotes the basal metabolic rate, Q the total fluid flow, and N the number of minimal tubules,
Non-power-law scaling edit
Closer analysis suggests that Kleiber's law can vary within and between species. Metabolic rates for smaller animals (birds under 10 kg [22 lb], or insects) typically fit to 2⁄3 much better than 3⁄4; for larger animals, the reverse holds.[12] As a result, log-log plots of metabolic rate versus body mass appear to "curve" upward, and fit better to quadratic models.[13] In all cases, local fits exhibit exponents in the [2⁄3,3⁄4] range.[14]
Modified circulatory models edit
Adjustments to the WBE model that retain assumptions of network shape predict larger scaling exponents, worsening the discrepancy with observed data.[15] But one can retain a similar theory by relaxing WBE's assumption of a nutrient transport network that is both fractal and circulatory. Different networks are less efficient, in that they exhibit a lower scaling exponent, but a metabolic rate determined by nutrient transport will always exhibit scaling between 2⁄3 and 3⁄4.[14] (WBE argued that fractal circulatory networks would necessarily evolve to minimize energy used for transport, but other researchers argue that their derivation contains subtle errors.[12][16]) If larger metabolic rates are evolutionarily favored, then low-mass organisms will prefer to arrange their networks to scale as 2⁄3, but large-mass organisms will prefer to arrange their networks as 3⁄4, which produces the observed curvature.[17]
Modified thermodynamic models edit
An alternative model notes that metabolic rate does not solely serve to generate heat. Metabolic rate contributing solely to useful work should scale with power 1 (linearly), whereas metabolic rate contributing to heat generation should be limited by surface area and scale with power 2⁄3. Basal metabolic rate is then the convex combination of these two effects: if the proportion of useful work is f, then the basal metabolic rate should scale as
Criticism of explanations edit
Kozłowski and Konarzewski have argued that attempts to explain Kleiber's law via any sort of limiting factor is flawed, because metabolic rates vary by factors of 4-5 between rest and activity. Hence any limits that affect the scaling of basal metabolic rate would in fact make elevated metabolism — and hence all animal activity — impossible.[20] WBE conversely argue that animals may well optimize for minimal transport energy dissipation during rest, without abandoning the ability for less efficient function at other times.[21]
Other researchers have also noted that Kozłowski and Konarzewski's criticism of the law tends to focus on precise structural details of the WBE circulatory networks, but that the latter are not essential to the model.[10]
Experimental support edit
Analyses of variance for a variety of physical variables suggest that although most variation in basal metabolic rate is determined by mass, additional variables with significant effects include body temperature and taxonomic order.[22][23]
A 1932 work by Brody calculated that the scaling was approximately 0.73.[8][24]
A 2004 analysis of field metabolic rates for mammals conclude that they appear to scale with exponent 0.749.[17]
Generalizations edit
Kleiber's law has been reported to interspecific comparisons and has been claimed not to apply at the intraspecific level.[25] The taxonomic level that body mass metabolic allometry should be studied has been debated.[26][27] Nonetheless, several analyses suggest that while the exponents of the Kleiber's relationship between body size and metabolism can vary at the intraspecific level, statistically, intraspecific exponents in both plants and animals tend to cluster around 3/4.[28]
In other kingdoms edit
A 1999 analysis concluded that biomass production in a given plant scaled with the 3⁄4 power of the plant's mass during the plant's growth,[29] but a 2001 paper that included various types of unicellular photosynthetic organisms found scaling exponents intermediate between 0.75 and 1.00.[30]
A 2006 paper in Nature argued that the exponent of mass is close to 1 for plant seedlings, but that variation between species, phyla, and growth conditions overwhelm any "Kleiber's law"-like effects.[31]
Intra-organismal results edit
Because cell protoplasm appears to have constant density across a range of organism masses, a consequence of Kleiber's law is that, in larger species, less energy is available to each cell volume. Cells appear to cope with this difficulty via choosing one of the following two strategies: smaller cells or a slower cellular metabolic rate. Neurons and adipocytes exhibit the former; every other type of cell, the latter.[32] As a result, different organs exhibit different allometric scalings (see table).[8]
Allometric scalings for BMR-vs.-mass in human tissue Organ Scaling exponent Brain 0.7 Kidney 0.85 Liver 0.87 Heart 0.98 Muscle 1.0 Skeleton 1.1
See also edit
References edit
- ^ Kleiber M (October 1947). "Body size and metabolic rate". Physiological Reviews. 27 (4): 511–41. doi:10.1152/physrev.1947.27.4.511. PMID 20267758.
- ^ a b c Kleiber M (January 1932). "Body size and metabolism". Hilgardia. 6 (11): 315–353. doi:10.3733/hilg.v06n11p315.
- ^ Enquist BJ, Brown JH, West GB (1998). "Allometric scaling of plant energetics and population density". Nature. 395 (10): 163–165. Bibcode:1998Natur.395..163E. doi:10.1038/25977.
- ^ Schmidt-Nielsen K (1984). Scaling: Why is animal size so important?. NY, NY: Cambridge University Press. ISBN 978-0521266574.
- ^ Harris JA, Benedict, FG (1919). "A biometric study of basal metabolism in man". Carnegie Inst. Of Wash. 6 (279): 31–266.
- ^ Thompson, D. W. (1917). On Growth and Form. Cambridge University Press.
- ^ Rubner M (1883). "Über den Einfluss der Körpergrosse auf Stoff- und Kraftwechsel". Zeitschr. F. BioI. 19: 535–562.
- ^ a b c Hulbert AJ (28 April 2014). "A Sceptics View: "Kleiber's Law" or the "3/4 Rule" is neither a Law nor a Rule but Rather an Empirical Approximation". Systems. 2 (2): 186–202. doi:10.3390/systems2020186.
- ^ a b West GB, Brown JH, Enquist BJ (April 1997). "A general model for the origin of allometric scaling laws in biology". Science. 276 (5309): 122–6. doi:10.1126/science.276.5309.122. PMID 9082983. S2CID 3140271.
- ^ a b Etienne RS, Apol ME, Olff HA (2006). "Demystifying the West, Brown & Enquist model of the allometry of metabolism". Functional Ecology. 20 (2): 394–399. Bibcode:2006FuEco..20..394E. doi:10.1111/j.1365-2435.2006.01136.x.
- ^ Painter PR, Edén P, Bengtsson HU (August 2006). "Pulsatile blood flow, shear force, energy dissipation and Murray's Law". Theoretical Biology & Medical Modelling. 3 (1): 31. doi:10.1186/1742-4682-3-31. PMC 1590016. PMID 16923189.
- ^ a b Dodds PS, Rothman DH, Weitz JS (March 2001). "Re-examination of the "3/4-law" of metabolism". Journal of Theoretical Biology. 209 (1): 9–27. arXiv:physics/0007096. Bibcode:2001JThBi.209....9D. doi:10.1006/jtbi.2000.2238. PMID 11237567. S2CID 9168199.
- ^ Kolokotrones T, Deeds EJ, Fontana W (April 2010). "Curvature in metabolic scaling". Nature. 464 (7289): 753–6. Bibcode:2010Natur.464..753K. doi:10.1038/nature08920. PMID 20360740. S2CID 4374163.
But note that a quadratic curve has undesirable theoretical implications; see MacKay NJ (July 2011). "Mass scale and curvature in metabolic scaling. Comment on: T. Kolokotrones et al., curvature in metabolic scaling, Nature 464 (2010) 753-756". Journal of Theoretical Biology. 280 (1): 194–6. Bibcode:2011JThBi.280..194M. doi:10.1016/j.jtbi.2011.02.011. PMID 21335012. - ^ a b Banavar JR, Moses ME, Brown JH, Damuth J, Rinaldo A, Sibly RM, Maritan A (September 2010). "A general basis for quarter-power scaling in animals". Proceedings of the National Academy of Sciences of the United States of America. 107 (36): 15816–20. Bibcode:2010PNAS..10715816B. doi:10.1073/pnas.1009974107. PMC 2936637. PMID 20724663.
- ^ Savage VM, Deeds EJ, Fontana W (September 2008). "Sizing up allometric scaling theory". PLOS Computational Biology. 4 (9): e1000171. Bibcode:2008PLSCB...4E0171S. doi:10.1371/journal.pcbi.1000171. PMC 2518954. PMID 18787686.
- ^ Apol ME, Etienne RS, Olff H (2008). "Revisiting the evolutionary origin of allometric metabolic scaling in biology". Functional Ecology. 22 (6): 1070–1080. Bibcode:2008FuEco..22.1070A. doi:10.1111/j.1365-2435.2008.01458.x.
- ^ a b Savage VM, Gillooly JF, Woodruff WH, West GB, Allen AP, Enquist BJ, Brown JH (April 2004). "The predominance of quarter-power scaling in biology". Functional Ecology. 18 (2): 257–282. Bibcode:2004FuEco..18..257S. doi:10.1111/j.0269-8463.2004.00856.x.
The original paper by West et al. (1997), which derives a model for the mammalian arterial system, predicts that smaller mammals should show consistent deviations in the direction of higher metabolic rates than expected from M3⁄4 scaling. Thus, metabolic scaling relationships are predicted to show a slight curvilinearity at the smallest size range.
- ^ a b Ballesteros FJ, Martinez VJ, Luque B, Lacasa L, Valor E, Moya A (January 2018). "On the thermodynamic origin of metabolic scaling". Scientific Reports. 8 (1): 1448. Bibcode:2018NatSR...8.1448B. doi:10.1038/s41598-018-19853-6. PMC 5780499. PMID 29362491.
- ^ Zotin AI (1990). Thermodynamic Bases of Biological Processes: Physiological Reactions and Adaptations. Walter de Gruyter. ISBN 9783110114010.
- ^ Kozlowski J, Konarzewski M (2004). "Is West, Brown and Enquist's model of allometric scaling mathematically correct and biologically relevant?". Functional Ecology. 18 (2): 283–9. Bibcode:2004FuEco..18..283K. doi:10.1111/j.0269-8463.2004.00830.x.
- ^ Brown JH, West GB, Enquist BJ (2005). "Yes, West, Brown and Enquist's model of allometric scaling is both mathematically correct and biologically relevant". Functional Ecology. 19 (4): 735–738. doi:10.1111/j.1365-2435.2005.01022.x.
- ^ Clarke A, Rothery P, Isaac NJ (May 2010). "Scaling of basal metabolic rate with body mass and temperature in mammals". The Journal of Animal Ecology. 79 (3): 610–9. Bibcode:2010JAnEc..79..610C. doi:10.1111/j.1365-2656.2010.01672.x. PMID 20180875.
- ^ Hayssen V, Lacy RC (1985). "Basal metabolic rates in mammals: taxonomic differences in the allometry of BMR and body mass". Comparative Biochemistry and Physiology. A, Comparative Physiology. 81 (4): 741–54. doi:10.1016/0300-9629(85)90904-1. PMID 2863065.
- ^ Brody S (1945). Bioenergetics and Growth. NY, NY: Reinhold.
- ^ Heusner AA (1982-04-01). "Energy metabolism and body size I. Is the 0.75 mass exponent of Kleiber's equation a statistical artifact?". Respiration Physiology. 48 (1): 1–12. doi:10.1016/0034-5687(82)90046-9. ISSN 0034-5687. PMID 7111915.
- ^ White CR, Blackburn TM, Seymour RS (October 2009). "Phylogenetically informed analysis of the allometry of Mammalian Basal metabolic rate supports neither geometric nor quarter-power scaling". Evolution; International Journal of Organic Evolution. 63 (10): 2658–67. doi:10.1111/j.1558-5646.2009.00747.x. PMID 19519636. S2CID 16889020.
- ^ Sieg AE, O'Connor MP, McNair JN, Grant BW, Agosta SJ, Dunham AE (November 2009). "Mammalian metabolic allometry: do intraspecific variation, phylogeny, and regression models matter?". The American Naturalist. 174 (5): 720–33. doi:10.1086/606023. PMID 19799501. S2CID 36468932.
- ^ Moses ME, Hou C, Woodruff WH, West GB, Nekola JC, Zuo W, Brown JH (2008). "Revisiting a model of ontogenetic growth: estimating model parameters from theory and data". The American Naturalist. 171 (5): 632–645. doi:10.1086/587073. PMID 18419571.
- ^ Enquist BJ, West GB, Charnov EL, Brown JH (28 October 1999). "Allometric scaling of production and life-history variation in vascular plants". Nature. 401 (6756): 907–911. Bibcode:1999Natur.401..907E. doi:10.1038/44819. ISSN 1476-4687. S2CID 4397261.
Corrigendum published 7 December 2000. - ^ Niklas KJ (2006). "A phyletic perspective on the allometry of plant biomass-partitioning patterns and functionally equivalent organ-categories". The New Phytologist. 171 (1): 27–40. doi:10.1111/j.1469-8137.2006.01760.x. PMID 16771980.
- ^ Reich PB, Tjoelker MG, Machado JL, Oleksyn J (January 2006). "Universal scaling of respiratory metabolism, size and nitrogen in plants". Nature. 439 (7075): 457–61. Bibcode:2006Natur.439..457R. doi:10.1038/nature04282. hdl:11299/176835. PMID 16437113. S2CID 1484450.
For a contrary view, see Enquist BJ, Allen AP, Brown JH, Gillooly JF, Kerkhoff AJ, Niklas KJ, Price CA, West GB (February 2007). "Biological scaling: does the exception prove the rule?". Nature. 445 (7127): E9–10, discussion E10–1. Bibcode:2007Natur.445....9E. doi:10.1038/nature05548. PMID 17268426. S2CID 43905935. and associated responses. - ^ Savage VM, Allen AP, Brown JH, Gillooly JF, Herman AB, Woodruff WH, West GB (March 2007). "Scaling of number, size, and metabolic rate of cells with body size in mammals". Proceedings of the National Academy of Sciences of the United States of America. 104 (11): 4718–23. Bibcode:2007PNAS..104.4718S. doi:10.1073/pnas.0611235104. PMC 1838666. PMID 17360590.
Further reading edit
- Rau AR (September 2002). "Biological scaling and physics". Journal of Biosciences. 27 (5): 475–8. doi:10.1007/BF02705043. PMID 12381870. S2CID 23900176.
- Wang Z, O'Connor TP, Heshka S, Heymsfield SB (November 2001). "The reconstruction of Kleiber's law at the organ-tissue level". The Journal of Nutrition. 131 (11): 2967–70. doi:10.1093/jn/131.11.2967. PMID 11694627.
- Whitfield J (2006). In the Beat of a Heart. Washington, D.C.: Joseph Henry Press. ISBN 9780309096812.
- Glazier DS (February 2010). "A unifying explanation for diverse metabolic scaling in animals and plants". Biological Reviews of the Cambridge Philosophical Society. 85 (1): 111–38. doi:10.1111/j.1469-185X.2009.00095.x. PMID 19895606. S2CID 28572410.
- Glazier DS (1 October 2014). "Metabolic Scaling in Complex Living Systems". Systems. 2 (4): 451–540. doi:10.3390/systems2040451.
- Johnson G (12 January 1999). "Of mice and Elephants". Archived from the original on 3 December 2008.
- Woolley T. "3/4 and Kleiber's Law". Numberphile. Brady Haran. Archived from the original on 2017-05-22. Retrieved 2013-04-01.


