
Summary
In mathematics, a linear equation is an equation that may be put in the form where are the variables (or unknowns), and are the coefficients, which are often real numbers. The coefficients may be considered as parameters of the equation and may be arbitrary expressions, provided they do not contain any of the variables. To yield a meaningful equation, the coefficients are required to not all be zero.
Alternatively, a linear equation can be obtained by equating to zero a linear polynomial over some field, from which the coefficients are taken.
The solutions of such an equation are the values that, when substituted for the unknowns, make the equality true.
In the case of just one variable, there is exactly one solution (provided that ). Often, the term linear equation refers implicitly to this particular case, in which the variable is sensibly called the unknown.
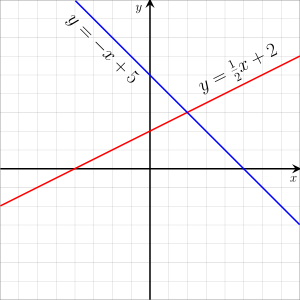
In the case of two variables, each solution may be interpreted as the Cartesian coordinates of a point of the Euclidean plane. The solutions of a linear equation form a line in the Euclidean plane, and, conversely, every line can be viewed as the set of all solutions of a linear equation in two variables. This is the origin of the term linear for describing this type of equation. More generally, the solutions of a linear equation in n variables form a hyperplane (a subspace of dimension n − 1) in the Euclidean space of dimension n.
Linear equations occur frequently in all mathematics and their applications in physics and engineering, partly because non-linear systems are often well approximated by linear equations.
This article considers the case of a single equation with coefficients from the field of real numbers, for which one studies the real solutions. All of its content applies to complex solutions and, more generally, to linear equations with coefficients and solutions in any field. For the case of several simultaneous linear equations, see system of linear equations.
One variable edit
A linear equation in one variable x can be written as with .
The solution is .
Two variables edit
A linear equation in two variables x and y can be written as with a and b not both 0.[1]
If a and b are real numbers, it has infinitely many solutions.
Linear function edit
If b ≠ 0, the equation
is a linear equation in the single variable y for every value of x. It has therefore a unique solution for y, which is given by
This defines a function. The graph of this function is a line with slope and y-intercept The functions whose graph is a line are generally called linear functions in the context of calculus. However, in linear algebra, a linear function is a function that maps a sum to the sum of the images of the summands. So, for this definition, the above function is linear only when c = 0, that is when the line passes through the origin. To avoid confusion, the functions whose graph is an arbitrary line are often called affine functions, and the linear functions such that c = 0 are often called linear maps.
Geometric interpretation edit
Each solution (x, y) of a linear equation
may be viewed as the Cartesian coordinates of a point in the Euclidean plane. With this interpretation, all solutions of the equation form a line, provided that a and b are not both zero. Conversely, every line is the set of all solutions of a linear equation.
The phrase "linear equation" takes its origin in this correspondence between lines and equations: a linear equation in two variables is an equation whose solutions form a line.
If b ≠ 0, the line is the graph of the function of x that has been defined in the preceding section. If b = 0, the line is a vertical line (that is a line parallel to the y-axis) of equation which is not the graph of a function of x.
Similarly, if a ≠ 0, the line is the graph of a function of y, and, if a = 0, one has a horizontal line of equation
Equation of a line edit
There are various ways of defining a line. In the following subsections, a linear equation of the line is given in each case.
Slope–intercept form or Gradient-intercept form edit
A non-vertical line can be defined by its slope m, and its y-intercept y0 (the y coordinate of its intersection with the y-axis). In this case, its linear equation can be written
If, moreover, the line is not horizontal, it can be defined by its slope and its x-intercept x0. In this case, its equation can be written
or, equivalently,
These forms rely on the habit of considering a nonvertical line as the graph of a function.[2] For a line given by an equation
these forms can be easily deduced from the relations
Point–slope form or Point-gradient form edit
A non-vertical line can be defined by its slope m, and the coordinates of any point of the line. In this case, a linear equation of the line is
or
This equation can also be written
for emphasizing that the slope of a line can be computed from the coordinates of any two points.
Intercept form edit
A line that is not parallel to an axis and does not pass through the origin cuts the axes into two different points. The intercept values x0 and y0 of these two points are nonzero, and an equation of the line is[3]
(It is easy to verify that the line defined by this equation has x0 and y0 as intercept values).
Two-point form edit
Given two different points (x1, y1) and (x2, y2), there is exactly one line that passes through them. There are several ways to write a linear equation of this line.
If x1 ≠ x2, the slope of the line is Thus, a point-slope form is[3]
By clearing denominators, one gets the equation
which is valid also when x1 = x2 (for verifying this, it suffices to verify that the two given points satisfy the equation).
This form is not symmetric in the two given points, but a symmetric form can be obtained by regrouping the constant terms:
(exchanging the two points changes the sign of the left-hand side of the equation).
Determinant form edit
The two-point form of the equation of a line can be expressed simply in terms of a determinant. There are two common ways for that.
The equation is the result of expanding the determinant in the equation
The equation can be obtained by expanding with respect to its first row the determinant in the equation
Besides being very simple and mnemonic, this form has the advantage of being a special case of the more general equation of a hyperplane passing through n points in a space of dimension n – 1. These equations rely on the condition of linear dependence of points in a projective space.
More than two variables edit
A linear equation with more than two variables may always be assumed to have the form
The coefficient b, often denoted a0 is called the constant term (sometimes the absolute term in old books[4][5]). Depending on the context, the term coefficient can be reserved for the ai with i > 0.
When dealing with variables, it is common to use and instead of indexed variables.
A solution of such an equation is a n-tuple such that substituting each element of the tuple for the corresponding variable transforms the equation into a true equality.
For an equation to be meaningful, the coefficient of at least one variable must be non-zero. If every variable has a zero coefficient, then, as mentioned for one variable, the equation is either inconsistent (for b ≠ 0) as having no solution, or all n-tuples are solutions.
The n-tuples that are solutions of a linear equation in n variables are the Cartesian coordinates of the points of an (n − 1)-dimensional hyperplane in an n-dimensional Euclidean space (or affine space if the coefficients are complex numbers or belong to any field). In the case of three variables, this hyperplane is a plane.
If a linear equation is given with aj ≠ 0, then the equation can be solved for xj, yielding
If the coefficients are real numbers, this defines a real-valued function of n real variables.
See also edit
Notes edit
- ^ Barnett, Ziegler & Byleen 2008, pg. 15
- ^ Larson & Hostetler 2007, p. 25
- ^ a b Wilson & Tracey 1925, pp. 52-53
- ^ Charles Hiram Chapman (1892). An Elementary Course in Theory of Equations. J. Wiley & sons. p. 17. Extract of page 17
- ^ David Martin Sensenig (1890). Numbers Universalized: An Advanced Algebra. American Book Company. p. 113. Extract of page 113
References edit
- Barnett, R.A.; Ziegler, M.R.; Byleen, K.E. (2008), College Mathematics for Business, Economics, Life Sciences and the Social Sciences (11th ed.), Upper Saddle River, N.J.: Pearson, ISBN 978-0-13-157225-6
- Larson, Ron; Hostetler, Robert (2007), Precalculus:A Concise Course, Houghton Mifflin, ISBN 978-0-618-62719-6
- Wilson, W.A.; Tracey, J.I. (1925), Analytic Geometry (revised ed.), D.C. Heath
External links edit
- "Linear equation", Encyclopedia of Mathematics, EMS Press, 2001 [1994]







