
Summary
The nuclear force (or nucleon–nucleon interaction, residual strong force, or, historically, strong nuclear force) is a force that acts between hadrons, most commonly observed between protons and neutrons of atoms. Neutrons and protons, both nucleons, are affected by the nuclear force almost identically. Since protons have charge +1 e, they experience an electric force that tends to push them apart, but at short range the attractive nuclear force is strong enough to overcome the electrostatic force. The nuclear force binds nucleons into atomic nuclei.
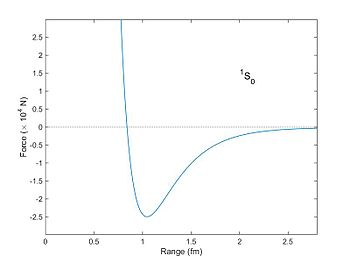
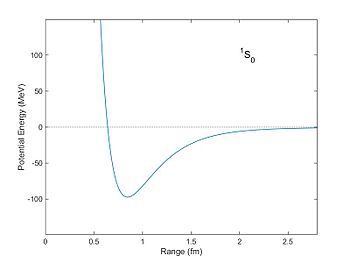
The nuclear force is powerfully attractive between nucleons at distances of about 0.8 femtometre (fm, or 0.8×10−15 m), but it rapidly decreases to insignificance at distances beyond about 2.5 fm. At distances less than 0.7 fm, the nuclear force becomes repulsive. This repulsion is responsible for the size of nuclei, since nucleons can come no closer than the force allows. (The size of an atom, of size in the order of angstroms (Å, or 10−10 m), is five orders of magnitude larger.) The nuclear force is not simple, though, as it depends on the nucleon spins, has a tensor component, and may depend on the relative momentum of the nucleons.[2]
The nuclear force has an essential role in storing energy that is used in nuclear power and nuclear weapons. Work (energy) is required to bring charged protons together against their electric repulsion. This energy is stored when the protons and neutrons are bound together by the nuclear force to form a nucleus. The mass of a nucleus is less than the sum total of the individual masses of the protons and neutrons. The difference in masses is known as the mass defect, which can be expressed as an energy equivalent. Energy is released when a heavy nucleus breaks apart into two or more lighter nuclei. This energy is the internucleon potential energy that is released when the nuclear force no longer holds the charged nuclear fragments together.[3][4]
A quantitative description of the nuclear force relies on equations that are partly empirical. These equations model the internucleon potential energies, or potentials. (Generally, forces within a system of particles can be more simply modelled by describing the system's potential energy; the negative gradient of a potential is equal to the vector force.) The constants for the equations are phenomenological, that is, determined by fitting the equations to experimental data. The internucleon potentials attempt to describe the properties of nucleon–nucleon interaction. Once determined, any given potential can be used in, e.g., the Schrödinger equation to determine the quantum mechanical properties of the nucleon system.
The discovery of the neutron in 1932 revealed that atomic nuclei were made of protons and neutrons, held together by an attractive force. By 1935 the nuclear force was conceived to be transmitted by particles called mesons. This theoretical development included a description of the Yukawa potential, an early example of a nuclear potential. Pions, fulfilling the prediction, were discovered experimentally in 1947. By the 1970s, the quark model had been developed, by which the mesons and nucleons were viewed as composed of quarks and gluons. By this new model, the nuclear force, resulting from the exchange of mesons between neighbouring nucleons, is a multiparticle interaction, the collective effect of strong force on the underlining structure of the nucleons.
Description edit
While the nuclear force is usually associated with nucleons, more generally this force is felt between hadrons, or particles composed of quarks. At small separations between nucleons (less than ~ 0.7 fm between their centres, depending upon spin alignment) the force becomes repulsive, which keeps the nucleons at a certain average separation. For identical nucleons (such as two neutrons or two protons) this repulsion arises from the Pauli exclusion force. A Pauli repulsion also occurs between quarks of the same flavour from different nucleons (a proton and a neutron).
Field strength edit
At distances larger than 0.7 fm the force becomes attractive between spin-aligned nucleons, becoming maximal at a centre–centre distance of about 0.9 fm. Beyond this distance the force drops exponentially, until beyond about 2.0 fm separation, the force is negligible. Nucleons have a radius of about 0.8 fm.[5]
At short distances (less than 1.7 fm or so), the attractive nuclear force is stronger than the repulsive Coulomb force between protons; it thus overcomes the repulsion of protons within the nucleus. However, the Coulomb force between protons has a much greater range as it varies as the inverse square of the charge separation, and Coulomb repulsion thus becomes the only significant force between protons when their separation exceeds about 2 to 2.5 fm.
The nuclear force has a spin-dependent component. The force is stronger for particles with their spins aligned than for those with their spins anti-aligned. If two particles are the same, such as two neutrons or two protons, the force is not enough to bind the particles, since the spin vectors of two particles of the same type must point in opposite directions when the particles are near each other and are (save for spin) in the same quantum state. This requirement for fermions stems from the Pauli exclusion principle. For fermion particles of different types, such as a proton and neutron, particles may be close to each other and have aligned spins without violating the Pauli exclusion principle, and the nuclear force may bind them (in this case, into a deuteron), since the nuclear force is much stronger for spin-aligned particles. But if the particles' spins are anti-aligned, the nuclear force is too weak to bind them, even if they are of different types.
The nuclear force also has a tensor component which depends on the interaction between the nucleon spins and the angular momentum of the nucleons, leading to deformation from a simple spherical shape.
Nuclear binding edit
To disassemble a nucleus into unbound protons and neutrons requires work against the nuclear force. Conversely, energy is released when a nucleus is created from free nucleons or other nuclei: the nuclear binding energy. Because of mass–energy equivalence (i.e. Einstein's formula E = mc2), releasing this energy causes the mass of the nucleus to be lower than the total mass of the individual nucleons, leading to the so-called "mass defect".[6]
The nuclear force is nearly independent of whether the nucleons are neutrons or protons. This property is called charge independence. The force depends on whether the spins of the nucleons are parallel or antiparallel, as it has a non-central or tensor component. This part of the force does not conserve orbital angular momentum, which under the action of central forces is conserved.
The symmetry resulting in the strong force, proposed by Werner Heisenberg, is that protons and neutrons are identical in every respect, other than their charge. This is not completely true, because neutrons are a tiny bit heavier, but it is an approximate symmetry. Protons and neutrons are therefore viewed as the same particle, but with different isospin quantum numbers; conventionally, the proton is isospin up, while the neutron is isospin down. The strong force is invariant under SU(2) isospin transformations, just as other interactions between particles are invariant under SU(2) transformations of intrinsic spin. In other words, both isospin and intrinsic spin transformations are isomorphic to the SU(2) symmetry group. There are only strong attractions when the total isospin of the set of interacting particles is 0, which is confirmed by experiment.[7]
Our understanding of the nuclear force is obtained by scattering experiments and the binding energy of light nuclei.
The nuclear force occurs by the exchange of virtual light mesons, such as the virtual pions, as well as two types of virtual mesons with spin (vector mesons), the rho mesons and the omega mesons. The vector mesons account for the spin-dependence of the nuclear force in this "virtual meson" picture.
The nuclear force is distinct from what historically was known as the weak nuclear force. The weak interaction is one of the four fundamental interactions, and plays a role in processes such as beta decay. The weak force plays no role in the interaction of nucleons, though it is responsible for the decay of neutrons to protons and vice versa.
History edit
The nuclear force has been at the heart of nuclear physics ever since the field was born in 1932 with the discovery of the neutron by James Chadwick. The traditional goal of nuclear physics is to understand the properties of atomic nuclei in terms of the "bare" interaction between pairs of nucleons, or nucleon–nucleon forces (NN forces).
Within months after the discovery of the neutron, Werner Heisenberg[8][9][10] and Dmitri Ivanenko[11] had proposed proton–neutron models for the nucleus.[12] Heisenberg approached the description of protons and neutrons in the nucleus through quantum mechanics, an approach that was not at all obvious at the time. Heisenberg's theory for protons and neutrons in the nucleus was a "major step toward understanding the nucleus as a quantum mechanical system".[13] Heisenberg introduced the first theory of nuclear exchange forces that bind the nucleons. He considered protons and neutrons to be different quantum states of the same particle, i.e., nucleons distinguished by the value of their nuclear isospin quantum numbers.
One of the earliest models for the nucleus was the liquid-drop model developed in the 1930s. One property of nuclei is that the average binding energy per nucleon is approximately the same for all stable nuclei, which is similar to a liquid drop. The liquid-drop model treated the nucleus as a drop of incompressible nuclear fluid, with nucleons behaving like molecules in a liquid. The model was first proposed by George Gamow and then developed by Niels Bohr, Werner Heisenberg, and Carl Friedrich von Weizsäcker. This crude model did not explain all the properties of the nucleus, but it did explain the spherical shape of most nuclei. The model also gave good predictions for the binding energy of nuclei.
In 1934, Hideki Yukawa made the earliest attempt to explain the nature of the nuclear force. According to his theory, massive bosons (mesons) mediate the interaction between two nucleons. In light of quantum chromodynamics (QCD)—and, by extension, the Standard Model—meson theory is no longer perceived as fundamental. But the meson-exchange concept (where hadrons are treated as elementary particles) continues to represent the best working model for a quantitative NN potential. The Yukawa potential (also called a screened Coulomb potential) is a potential of the form
where g is a magnitude scaling constant, i.e., the amplitude of potential, is the Yukawa particle mass, r is the radial distance to the particle. The potential is monotone increasing, implying that the force is always attractive. The constants are determined empirically. The Yukawa potential depends only on the distance r between particles, hence it models a central force.
Throughout the 1930s a group at Columbia University led by I. I. Rabi developed magnetic-resonance techniques to determine the magnetic moments of nuclei. These measurements led to the discovery in 1939 that the deuteron also possessed an electric quadrupole moment.[14][15] This electrical property of the deuteron had been interfering with the measurements by the Rabi group. The deuteron, composed of a proton and a neutron, is one of the simplest nuclear systems. The discovery meant that the physical shape of the deuteron was not symmetric, which provided valuable insight into the nature of the nuclear force binding nucleons. In particular, the result showed that the nuclear force was not a central force, but had a tensor character.[1] Hans Bethe identified the discovery of the deuteron's quadrupole moment as one of the important events during the formative years of nuclear physics.[14]
Historically, the task of describing the nuclear force phenomenologically was formidable. The first semi-empirical quantitative models came in the mid-1950s,[1] such as the Woods–Saxon potential (1954). There was substantial progress in experiment and theory related to the nuclear force in the 1960s and 1970s. One influential model was the Reid potential (1968)[1]
where and where the potential is given in units of MeV. In recent years,[when?] experimenters have concentrated on the subtleties of the nuclear force, such as its charge dependence, the precise value of the πNN coupling constant, improved phase-shift analysis, high-precision NN data, high-precision NN potentials, NN scattering at intermediate and high energies, and attempts to derive the nuclear force from QCD.[citation needed]
As a residual of strong force edit
The nuclear force is a residual effect of the more fundamental strong force, or strong interaction. The strong interaction is the attractive force that binds the elementary particles called quarks together to form the nucleons (protons and neutrons) themselves. This more powerful force, one of the fundamental forces of nature, is mediated by particles called gluons. Gluons hold quarks together through colour charge which is analogous to electric charge, but far stronger. Quarks, gluons, and their dynamics are mostly confined within nucleons, but residual influences extend slightly beyond nucleon boundaries to give rise to the nuclear force.
The nuclear forces arising between nucleons are analogous to the forces in chemistry between neutral atoms or molecules called London dispersion forces. Such forces between atoms are much weaker than the attractive electrical forces that hold the atoms themselves together (i.e., that bind electrons to the nucleus), and their range between atoms is shorter, because they arise from small separation of charges inside the neutral atom.[further explanation needed] Similarly, even though nucleons are made of quarks in combinations which cancel most gluon forces (they are "colour neutral"), some combinations of quarks and gluons nevertheless leak away from nucleons, in the form of short-range nuclear force fields that extend from one nucleon to another nearby nucleon. These nuclear forces are very weak compared to direct gluon forces ("colour forces" or strong forces) inside nucleons, and the nuclear forces extend only over a few nuclear diameters, falling exponentially with distance. Nevertheless, they are strong enough to bind neutrons and protons over short distances, and overcome the electrical repulsion between protons in the nucleus.
Sometimes, the nuclear force is called the residual strong force, in contrast to the strong interactions which arise from QCD. This phrasing arose during the 1970s when QCD was being established. Before that time, the strong nuclear force referred to the inter-nucleon potential. After the verification of the quark model, strong interaction has come to mean QCD.
Nucleon–nucleon potentials edit
Two-nucleon systems such as the deuteron, the nucleus of a deuterium atom, as well as proton–proton or neutron–proton scattering are ideal for studying the NN force. Such systems can be described by attributing a potential (such as the Yukawa potential) to the nucleons and using the potentials in a Schrödinger equation. The form of the potential is derived phenomenologically (by measurement), although for the long-range interaction, meson-exchange theories help to construct the potential. The parameters of the potential are determined by fitting to experimental data such as the deuteron binding energy or NN elastic scattering cross sections (or, equivalently in this context, so-called NN phase shifts).
The most widely used NN potentials are the Paris potential, the Argonne AV18 potential,[16] the CD-Bonn potential, and the Nijmegen potentials.
A more recent approach is to develop effective field theories for a consistent description of nucleon–nucleon and three-nucleon forces. Quantum hadrodynamics is an effective field theory of the nuclear force, comparable to QCD for colour interactions and QED for electromagnetic interactions. Additionally, chiral symmetry breaking can be analyzed in terms of an effective field theory (called chiral perturbation theory) which allows perturbative calculations of the interactions between nucleons with pions as exchange particles.
From nucleons to nuclei edit
The ultimate goal of nuclear physics would be to describe all nuclear interactions from the basic interactions between nucleons. This is called the microscopic or ab initio approach of nuclear physics. There are two major obstacles to overcome:
- Calculations in many-body systems are difficult (because of multi-particle interactions) and require advanced computation techniques.
- There is evidence that three-nucleon forces (and possibly higher multi-particle interactions) play a significant role. This means that three-nucleon potentials must be included into the model.
This is an active area of research with ongoing advances in computational techniques leading to better first-principles calculations of the nuclear shell structure. Two- and three-nucleon potentials have been implemented for nuclides up to A = 12.
Nuclear potentials edit
A successful way of describing nuclear interactions is to construct one potential for the whole nucleus instead of considering all its nucleon components. This is called the macroscopic approach. For example, scattering of neutrons from nuclei can be described by considering a plane wave in the potential of the nucleus, which comprises a real part and an imaginary part. This model is often called the optical model since it resembles the case of light scattered by an opaque glass sphere.
Nuclear potentials can be local or global: local potentials are limited to a narrow energy range and/or a narrow nuclear mass range, while global potentials, which have more parameters and are usually less accurate, are functions of the energy and the nuclear mass and can therefore be used in a wider range of applications.
See also edit
- Physics portal
- Nuclear binding energy
References edit
- ^ a b c d Reid, R. V. (1968). "Local phenomenological nucleon–nucleon potentials". Annals of Physics. 50 (3): 411–448. Bibcode:1968AnPhy..50..411R. doi:10.1016/0003-4916(68)90126-7.
- ^ Kenneth S. Krane (1988). Introductory Nuclear Physics. Wiley & Sons. ISBN 0-471-80553-X.
- ^ Binding Energy, Mass Defect Archived 2017-06-18 at the Wayback Machine, Furry Elephant physics educational site, retrieved 2012-07-01.
- ^ Chapter 4. NUCLEAR PROCESSES, THE STRONG FORCE Archived 2013-09-03 at the Wayback Machine, M. Ragheb, 1/30/2013, University of Illinois.
- ^ Povh, B.; Rith, K.; Scholz, C.; Zetsche, F. (2002). Particles and Nuclei: An Introduction to the Physical Concepts. Berlin: Springer-Verlag. p. 73. ISBN 978-3-540-43823-6.
- ^ Stern, Dr. Swapnil Nikam (February 11, 2009). "Nuclear Binding Energy". From Stargazers to Starships. NASA website. Archived from the original on 2016-04-09. Retrieved 2010-12-30.
- ^ Griffiths, David, Introduction to Elementary Particles
- ^ Heisenberg, W. (1932). "Über den Bau der Atomkerne. I". Z. Phys. (in German). 77 (1–2): 1–11. Bibcode:1932ZPhy...77....1H. doi:10.1007/BF01342433. S2CID 186218053.
- ^ Heisenberg, W. (1932). "Über den Bau der Atomkerne. II". Z. Phys. (in German). 78 (3–4): 156–164. Bibcode:1932ZPhy...78..156H. doi:10.1007/BF01337585. S2CID 186221789.
- ^ Heisenberg, W. (1933). "Über den Bau der Atomkerne. III". Z. Phys. (in German). 80 (9–10): 587–596. Bibcode:1933ZPhy...80..587H. doi:10.1007/BF01335696. S2CID 126422047.
- ^ Iwanenko, D. D., The neutron hypothesis, Nature 129 (1932) 798.
- ^ Miller A. I. Early Quantum Electrodynamics: A Sourcebook, Cambridge University Press, Cambridge, 1995, ISBN 0521568919, pp. 84–88.
- ^ Brown, L. M.; Rechenberg, H. (1996). The Origin of the Concept of Nuclear Forces. Bristol and Philadelphia: Institute of Physics Publishing. ISBN 0750303735. Archived from the original on 2023-12-30. Retrieved 2020-10-19.
- ^ a b John S. Rigden (1987). Rabi, Scientist and Citizen. New York: Basic Books, Inc. pp. 99–114. ISBN 9780674004351. Archived from the original on December 30, 2023. Retrieved May 9, 2015.
- ^ Kellogg, J. M.; Rabi, I. I.; Ramsey, N. F.; Zacharias, J. R. (1939). "An electrical quadrupole moment of the deuteron". Physical Review. 55 (3): 318–319. Bibcode:1939PhRv...55..318K. doi:10.1103/physrev.55.318. Archived from the original on May 12, 2017. Retrieved May 9, 2015.
- ^ Wiringa, R. B.; Stoks, V. G. J.; Schiavilla, R. (1995). "Accurate nucleon–nucleon potential with charge-independence breaking". Physical Review C. 51 (1): 38–51. arXiv:nucl-th/9408016. Bibcode:1995PhRvC..51...38W. doi:10.1103/PhysRevC.51.38. PMID 9970037. S2CID 118937727.
Bibliography edit
- Gerald Edward Brown and A. D. Jackson (1976). The Nucleon–Nucleon Interaction. Amsterdam North-Holland Publishing. ISBN 0-7204-0335-9.
- R. Machleidt and I. Slaus, "The nucleon–nucleon interaction" Archived 2021-05-07 at the Wayback Machine, J. Phys. G 27 (May 2001) R69. doi:10.1088/0954-3899/27/5/201. (Topical review.)
- E. A. Nersesov (1990). Fundamentals of atomic and nuclear physics. Moscow: Mir Publishers. ISBN 5-06-001249-2.
- Navrátil, Petr; Ormand, W. Erich (2003). "Ab initio shell model with a genuine three-nucleon force for the p-shell nuclei". Physical Review C. 68 (3): 034305. arXiv:nucl-th/0305090. Bibcode:2003PhRvC..68c4305N. doi:10.1103/PhysRevC.68.034305. S2CID 119091461.
Further reading edit
- Ruprecht Machleidt, "Nuclear Forces", Scholarpedia, 9(1):30710. doi:10.4249/scholarpedia.30710.


