
Summary
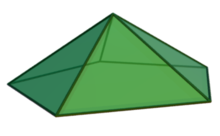
In geometry, a pentagonal pyramid is a pyramid with a pentagonal base upon which are erected five triangular faces that meet at a point (the apex). Like any pyramid, it is self-dual.
| Pentagonal pyramid | |
|---|---|
 | |
| Type | Johnson J1 – J2 – J3 |
| Faces | 5 triangles 1 pentagon |
| Edges | 10 |
| Vertices | 6 |
| Vertex configuration | 5(32.5) (35) |
| Schläfli symbol | ( ) ∨ {5} |
| Symmetry group | C5v, [5], (*55) |
| Rotation group | C5, [5]+, (55) |
| Dual polyhedron | self |
| Properties | convex |
| Net | |
 | |

The regular pentagonal pyramid has a base that is a regular pentagon and lateral faces that are equilateral triangles. It is one of the Johnson solids (J2).
It can be seen as the "lid" of an icosahedron; the rest of the icosahedron forms a gyroelongated pentagonal pyramid, J11.
More generally an order-2 vertex-uniform pentagonal pyramid can be defined with a regular pentagonal base and 5 isosceles triangle sides of any height.
Cartesian coordinates edit
The pentagonal pyramid can be seen as the "lid" of a regular icosahedron; the rest of the icosahedron forms a gyroelongated pentagonal pyramid, J11. From the Cartesian coordinates of the icosahedron, Cartesian coordinates for a pentagonal pyramid with edge length 2 may be inferred as
where 𝜏 (sometimes written as φ) is the golden ratio.[1]
The height H, from the midpoint of the pentagonal face to the apex, of a pentagonal pyramid with edge length a may therefore be computed as:
Its surface area A can be computed as the area of the pentagonal base plus five times the area of one triangle:
Its volume can be calculated as:
Related polyhedra edit
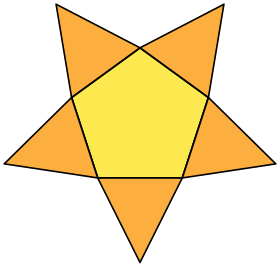
The pentagrammic star pyramid has the same vertex arrangement, but connected onto a pentagram base:
| Regular pyramids | ||||||||
|---|---|---|---|---|---|---|---|---|
| Digonal | Triangular | Square | Pentagonal | Hexagonal | Heptagonal | ... | ||
| Improper | Regular | Equilateral | Isosceles | |||||
| ... | ||||||||
| ... | ||||||||
| Pentagonal frustum is a pentagonal pyramid with its apex truncated |
The top of an icosahedron is a pentagonal pyramid |
Example edit
References edit
- ^ Weisstein, Eric W. "Icosahedral Group". mathworld.wolfram.com. Retrieved 2020-04-12.
- ^ a b Sapiña, R. "Area and volume of a pentagonal pyramid and Johnson solid J₂". Problemas y ecuaciones (in Spanish). ISSN 2659-9899. Retrieved 2020-06-29.
- ^ a b Weisstein, Eric W. "Pentagonal Pyramid". mathworld.wolfram.com. Retrieved 2020-04-12.
External links edit
- Weisstein, Eric W., "Pentagonal pyramid" ("Johnson solid") at MathWorld.
- Virtual Reality Polyhedra www.georgehart.com: The Encyclopedia of Polyhedra ( VRML model)


