Uniform pentagrammic crossed-antiprism
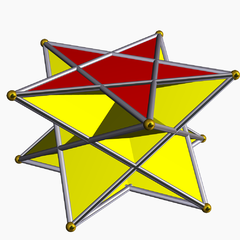
Type	Prismatic uniform polyhedron
Elements	F = 12, E = 20 V = 10 (χ = 2)
Faces by sides	10{3}+2{5/2}
Schläfli symbol	s{2,10/3} sr{2,5/3}
Wythoff symbol	| 2 2 5/3
Coxeter diagram	=
Symmetry	D5h, [5,2], (*522), order 20
Rotation group	D5, [5,2]+, (552), order 10 D5d
Index references	U80(a)
Dual	Pentagrammic concave trapezohedron
Properties	nonconvex
Vertex figure 3.3.3.5/3 or 3.3.3.-5/2

In geometry, the pentagrammic crossed-antiprism is one in an infinite set of nonconvex antiprisms formed by triangle sides and two regular star polygon caps, in this case two pentagrams.

It differs from the pentagrammic antiprism by having opposite orientations on the two pentagrams.

This polyhedron is identified with the indexed name U₈₀ as a uniform polyhedron.

An alternative representation with hollow pentagrams.

The pentagrammic crossed-antiprism may be inscribed within an icosahedron, and has ten triangular faces in common with the great icosahedron. It has the same vertex arrangement as the pentagonal antiprism. In fact, it may be considered as a parabidiminished great icosahedron.

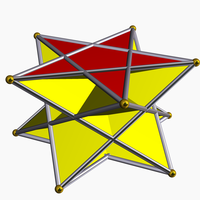Pentagrammic crossed-antiprism

Great icosahedron coloured with D5d symmetry