
Summary
In physics and materials science, plasticity (also known as plastic deformation) is the ability of a solid material to undergo permanent deformation, a non-reversible change of shape in response to applied forces.[1][2] For example, a solid piece of metal being bent or pounded into a new shape displays plasticity as permanent changes occur within the material itself. In engineering, the transition from elastic behavior to plastic behavior is known as yielding.

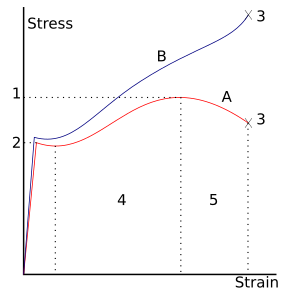
- Ultimate strength
- Yield strength (yield point)
- Rupture
- Strain hardening region
- Necking region
- Apparent stress (F/A0)
- Actual stress (F/A)
Plastic deformation is observed in most materials, particularly metals, soils, rocks, concrete, and foams.[3][4][5][6] However, the physical mechanisms that cause plastic deformation can vary widely. At a crystalline scale, plasticity in metals is usually a consequence of dislocations. Such defects are relatively rare in most crystalline materials, but are numerous in some and part of their crystal structure; in such cases, plastic crystallinity can result. In brittle materials such as rock, concrete and bone, plasticity is caused predominantly by slip at microcracks. In cellular materials such as liquid foams or biological tissues, plasticity is mainly a consequence of bubble or cell rearrangements, notably T1 processes.
For many ductile metals, tensile loading applied to a sample will cause it to behave in an elastic manner. Each increment of load is accompanied by a proportional increment in extension. When the load is removed, the piece returns to its original size. However, once the load exceeds a threshold – the yield strength – the extension increases more rapidly than in the elastic region; now when the load is removed, some degree of extension will remain.
Elastic deformation, however, is an approximation and its quality depends on the time frame considered and loading speed. If, as indicated in the graph opposite, the deformation includes elastic deformation, it is also often referred to as "elasto-plastic deformation" or "elastic-plastic deformation".
Perfect plasticity is a property of materials to undergo irreversible deformation without any increase in stresses or loads. Plastic materials that have been hardened by prior deformation, such as cold forming, may need increasingly higher stresses to deform further. Generally, plastic deformation is also dependent on the deformation speed, i.e. higher stresses usually have to be applied to increase the rate of deformation. Such materials are said to deform visco-plastically.
Contributing properties edit
The plasticity of a material is directly proportional to the ductility and malleability of the material.
Physical mechanisms edit
In metals edit
Plasticity in a crystal of pure metal is primarily caused by two modes of deformation in the crystal lattice: slip and twinning. Slip is a shear deformation which moves the atoms through many interatomic distances relative to their initial positions. Twinning is the plastic deformation which takes place along two planes due to a set of forces applied to a given metal piece.
Most metals show more plasticity when hot than when cold. Lead shows sufficient plasticity at room temperature, while cast iron does not possess sufficient plasticity for any forging operation even when hot. This property is of importance in forming, shaping and extruding operations on metals. Most metals are rendered plastic by heating and hence shaped hot.
Slip systems edit
Crystalline materials contain uniform planes of atoms organized with long-range order. Planes may slip past each other along their close-packed directions, as is shown on the slip systems page. The result is a permanent change of shape within the crystal and plastic deformation. The presence of dislocations increases the likelihood of planes.
Reversible plasticity edit
On the nanoscale the primary plastic deformation in simple face-centered cubic metals is reversible, as long as there is no material transport in form of cross-slip.[7] Shape-memory alloys such as Nitinol wire also exhibit a reversible form of plasticity which is more properly called pseudoelasticity.
Shear banding edit
The presence of other defects within a crystal may entangle dislocations or otherwise prevent them from gliding. When this happens, plasticity is localized to particular regions in the material. For crystals, these regions of localized plasticity are called shear bands.
Microplasticity edit
Microplasticity is a local phenomenon in metals. It occurs for stress values where the metal is globally in the elastic domain while some local areas are in the plastic domain.[8]
Amorphous materials edit
Crazing edit
In amorphous materials, the discussion of "dislocations" is inapplicable, since the entire material lacks long range order. These materials can still undergo plastic deformation. Since amorphous materials, like polymers, are not well-ordered, they contain a large amount of free volume, or wasted space. Pulling these materials in tension opens up these regions and can give materials a hazy appearance. This haziness is the result of crazing, where fibrils are formed within the material in regions of high hydrostatic stress. The material may go from an ordered appearance to a "crazy" pattern of strain and stretch marks.
Cellular materials edit
These materials plastically deform when the bending moment exceeds the fully plastic moment. This applies to open cell foams where the bending moment is exerted on the cell walls. The foams can be made of any material with a plastic yield point which includes rigid polymers and metals. This method of modeling the foam as beams is only valid if the ratio of the density of the foam to the density of the matter is less than 0.3. This is because beams yield axially instead of bending. In closed cell foams, the yield strength is increased if the material is under tension because of the membrane that spans the face of the cells.
Soils and sand edit
Soils, particularly clays, display a significant amount of inelasticity under load. The causes of plasticity in soils can be quite complex and are strongly dependent on the microstructure, chemical composition, and water content. Plastic behavior in soils is caused primarily by the rearrangement of clusters of adjacent grains.
Rocks and concrete edit
Inelastic deformations of rocks and concrete are primarily caused by the formation of microcracks and sliding motions relative to these cracks. At high temperatures and pressures, plastic behavior can also be affected by the motion of dislocations in individual grains in the microstructure.
Time-independent yielding and plastic flow in crystalline materials[9] edit
Time-independent plastic flow in both single crystals and polycrystals is defined by a critical/maximum resolved shear stress (τCRSS), initiating dislocation migration along parallel slip planes of a single slip system, thereby defining the transition from elastic to plastic deformation behavior in crystalline materials.
Time-independent yielding and plastic flow in single crystals edit
The critical resolved shear stress for single crystals is defined by Schmid’s law τCRSS=σy/m, where σy is the yield strength of the single crystal and m is the Schmid factor. The Schmid factor comprises two variables λ and φ, defining the angle between the slip plane direction and the tensile force applied, and the angle between the slip plane normal and the tensile force applied, respectively. Notably, because m > 1, σy > τCRSS.
Critical resolved shear stress dependence on temperature, strain rate, and point defects edit
There are three characteristic regions of the critical resolved shear stress as a function of temperature. In the low temperature region 1 (T ≤ 0.25Tm), the strain rate must be high to achieve high τCRSS which is required to initiate dislocation glide and equivalently plastic flow. In region 1, the critical resolved shear stress has two components: athermal (τa) and thermal (τ*) shear stresses, arising from the stress required to move dislocations in the presence of other dislocations, and the resistance of point defect obstacles to dislocation migration, respectively. At T = T*, the moderate temperature region 2 (0.25Tm < T < 0.7Tm) is defined, where the thermal shear stress component τ* → 0, representing the elimination of point defect impedance to dislocation migration. Thus the temperature-independent critical resolved shear stress τCRSS = τa remains so until region 3 is defined. Notably, in region 2 moderate temperature time-dependent plastic deformation (creep) mechanisms such as solute-drag should be considered. Furthermore, in the high temperature region 3 (T ≥ 0.7Tm) έ can be low, contributing to low τCRSS, however plastic flow will still occur due to thermally activated high temperature time-dependent plastic deformation mechanisms such as Nabarro–Herring (NH) and Coble diffusional flow through the lattice and along the single crystal surfaces, respectively, as well as dislocation climb-glide creep.
Stages of time-independent plastic flow, post yielding edit
During the easy glide stage 1, the work hardening rate, defined by the change in shear stress with respect to shear strain (dτ/dγ) is low, representative of a small amount of applied shear stress necessary to induce a large amount of shear strain. Facile dislocation glide and corresponding flow is attributed to dislocation migration along parallel slip planes only (i.e. one slip system). Moderate impedance to dislocation migration along parallel slip planes is exhibited according to the weak stress field interactions between these dislocations, which heightens with smaller interplanar spacing. Overall, these migrating dislocations within a single slip system act as weak obstacles to flow, and a modest rise in stress is observed in comparison to the yield stress. During the linear hardening stage 2 of flow, the work hardening rate becomes high as considerable stress is required to overcome the stress field interactions of dislocations migrating on non-parallel slip planes (i.e. multiple slip systems), acting as strong obstacles to flow. Much stress is required to drive continual dislocation migration for small strains. The shear flow stress is directly proportional to the square root of the dislocation density (τflow ~ρ½), irrespective of the evolution of dislocation configurations, displaying the reliance of hardening on the number of dislocations present. Regarding this evolution of dislocation configurations, at small strains the dislocation arrangement is a random 3D array of intersecting lines. Moderate strains correspond to cellular dislocation structures of heterogeneous dislocation distribution with large dislocation density at the cell boundaries, and small dislocation density within the cell interior. At even larger strains the cellular dislocation structure reduces in size until a minimum size is achieved. Finally, the work hardening rate becomes low again in the exhaustion/saturation of hardening stage 3 of plastic flow, as small shear stresses produce large shear strains. Notably, instances when multiple slip systems are oriented favorably with respect to the applied stress, the τCRSS for these systems may be similar and yielding may occur according to dislocation migration along multiple slip systems with non-parallel slip planes, displaying a stage 1 work-hardening rate typically characteristic of stage 2. Lastly, distinction between time-independent plastic deformation in body-centered cubic transition metals and face centered cubic metals is summarized below.
| Body-centered cubic transition metals | Face-centered cubic metals |
|---|---|
| Critical resolved shear stress = high (relatively) & strongly temperature-dependent | Critical resolved shear stress = low (relatively) & weakly temperature-dependent |
| Work hardening rate = temperature-independent | Work hardening rate = temperature-dependent |
| Necking strain increases with temperature | Necking strain decreases with temperature |
Time-independent yielding and plastic flow in polycrystals edit
Plasticity in polycrystals differs substantially from that in single crystals due to the presence of grain boundary (GB) planar defects, which act as very strong obstacles to plastic flow by impeding dislocation migration along the entire length of the activated slip plane(s). Hence, dislocations cannot pass from one grain to another across the grain boundary. The following sections explore specific GB requirements for extensive plastic deformation of polycrystals prior to fracture, as well as the influence of microscopic yielding within individual crystallites on macroscopic yielding of the polycrystal. The critical resolved shear stress for polycrystals is defined by Schmid’s law as well (τCRSS=σy/ṁ), where σy is the yield strength of the polycrystal and ṁ is the weighted Schmid factor. The weighted Schmid factor reflects the least favorably oriented slip system among the most favorably oriented slip systems of the grains constituting the GB.
Grain boundary constraint in polycrystals edit
The GB constraint for polycrystals can be explained by considering a grain boundary in the xz plane between two single crystals A and B of identical composition, structure, and slip systems, but misoriented with respect to each other. To ensure that voids do not form between individually deforming grains, the GB constraint for the bicrystal is as follows: εxxA = εxxB (the x-axial strain at the GB must be equivalent for A and B), εzzA = εzzB (the z-axial strain at the GB must be equivalent for A and B), and εxzA = εxzB (the xz shear strain along the xz-GB plane must be equivalent for A and B). In addition, this GB constraint requires that five independent slip systems be activated per crystallite constituting the GB. Notably, because independent slip systems are defined as slip planes on which dislocation migrations cannot be reproduced by any combination of dislocation migrations along other slip system’s planes, the number of geometrical slip systems for a given crystal system - which by definition can be constructed by slip system combinations - is typically greater than that of independent slip systems. Significantly, there is a maximum of five independent slip systems for each of the seven crystal systems, however, not all seven crystal systems acquire this upper limit. In fact, even within a given crystal system, the composition and Bravais lattice diversifies the number of independent slip systems (see the table below). In cases for which crystallites of a polycrystal do not obtain five independent slip systems, the GB condition cannot be met, and thus the time-independent deformation of individual crystallites results in cracks and voids at the GBs of the polycrystal, and soon fracture is realized. Hence, for a given composition and structure, a single crystal with less than five independent slip systems is stronger (exhibiting a greater extent of plasticity) than its polycrystalline form.
| Bravais lattice | Primary material class: # Independent slip systems |
|---|---|
| Face centered cubic | Metal: 5, ceramic (covalent): 5, ceramic (ionic): 2 |
| Body centered cubic | Metal: 5 |
| Simple cubic | Ceramic (ionic): 3 |
| Hexagonal | Metal: 2, ceramic (mixed): 2 |
Implications of the grain boundary constraint in polycrystals edit
Although the two crystallites A and B discussed in the above section have identical slip systems, they are misoriented with respect to each other, and therefore misoriented with respect to the applied force. Thus, microscopic yielding within a crystallite interior may occur according to the rules governing single crystal time-independent yielding. Eventually, the activated slip planes within the grain interiors will permit dislocation migration to the GB where many dislocations then pile up as geometrically necessary dislocations. This pile up corresponds to strain gradients across individual grains as the dislocation density near the GB is greater than that in the grain interior, imposing a stress on the adjacent grain in contact. When considering the AB bicrystal as a whole, the most favorably oriented slip system in A will not be the that in B, and hence τACRSS ≠ τBCRSS. Paramount is the fact that macroscopic yielding of the bicrystal is prolonged until the higher value of τCRSS between grains A and B is achieved, according to the GB constraint. Thus, for a given composition and structure, a polycrystal with five independent slip systems is stronger (greater extent of plasticity) than its single crystalline form. Correspondingly, the work hardening rate will be higher for the polycrystal than the single crystal, as more stress is required in the polycrystal to produce strains. Importantly, just as with single crystal flow stress, τflow ~ρ½, but is also inversely proportional to the square root of average grain diameter (τflow ~d-½ ). Therefore, the flow stress of a polycrystal, and hence the polycrystal’s strength, increases with small grain size. The reason for this is that smaller grains have a relatively smaller number of slip planes to be activated, corresponding to a fewer number of dislocations migrating to the GBs, and therefore less stress induced on adjacent grains due to dislocation pile up. In addition, for a given volume of polycrystal, smaller grains present more strong obstacle grain boundaries. These two factors provide an understanding as to why the onset of macroscopic flow in fine-grained polycrystals occurs at larger applied stresses than in coarse-grained polycrystals.
Mathematical descriptions edit
Deformation theory edit
There are several mathematical descriptions of plasticity.[12] One is deformation theory (see e.g. Hooke's law) where the Cauchy stress tensor (of order d-1 in d dimensions) is a function of the strain tensor. Although this description is accurate when a small part of matter is subjected to increasing loading (such as strain loading), this theory cannot account for irreversibility.
Ductile materials can sustain large plastic deformations without fracture. However, even ductile metals will fracture when the strain becomes large enough—this is as a result of work hardening of the material, which causes it to become brittle. Heat treatment such as annealing can restore the ductility of a worked piece, so that shaping can continue.
Flow plasticity theory edit
In 1934, Egon Orowan, Michael Polanyi and Geoffrey Ingram Taylor, roughly simultaneously, realized that the plastic deformation of ductile materials could be explained in terms of the theory of dislocations. The mathematical theory of plasticity, flow plasticity theory, uses a set of non-linear, non-integrable equations to describe the set of changes on strain and stress with respect to a previous state and a small increase of deformation.
Yield criteria edit
If the stress exceeds a critical value, as was mentioned above, the material will undergo plastic, or irreversible, deformation. This critical stress can be tensile or compressive. The Tresca and the von Mises criteria are commonly used to determine whether a material has yielded. However, these criteria have proved inadequate for a large range of materials and several other yield criteria are also in widespread use.
Tresca criterion edit
The Tresca criterion is based on the notion that when a material fails, it does so in shear, which is a relatively good assumption when considering metals. Given the principal stress state, we can use Mohr's circle to solve for the maximum shear stresses our material will experience and conclude that the material will fail if
where σ1 is the maximum normal stress, σ3 is the minimum normal stress, and σ0 is the stress under which the material fails in uniaxial loading. A yield surface may be constructed, which provides a visual representation of this concept. Inside of the yield surface, deformation is elastic. On the surface, deformation is plastic. It is impossible for a material to have stress states outside its yield surface.
Huber–von Mises criterion edit
The Huber–von Mises criterion[13] is based on the Tresca criterion but takes into account the assumption that hydrostatic stresses do not contribute to material failure. M. T. Huber was the first who proposed the criterion of shear energy.[14][15] Von Mises solves for an effective stress under uniaxial loading, subtracting out hydrostatic stresses, and states that all effective stresses greater than that which causes material failure in uniaxial loading will result in plastic deformation.
Again, a visual representation of the yield surface may be constructed using the above equation, which takes the shape of an ellipse. Inside the surface, materials undergo elastic deformation. Reaching the surface means the material undergoes plastic deformations.
See also edit
References edit
- ^ Lubliner, Jacob (2008). Plasticity theory. Dover. ISBN 978-0-486-46290-5.
- ^ Bigoni, Davide (2012). Nonlinear Solid Mechanics: Bifurcation Theory and Material Instability. Cambridge University Press. ISBN 978-1-107-02541-7.
- ^ Jirásek, Milan; Bažant, Zdeněk P. (2002). Inelastic analysis of structures. John Wiley and Sons. ISBN 0-471-98716-6.
- ^ Chen, Wai-Fah (2008). Limit Analysis and Soil Plasticity. J. Ross Publishing. ISBN 978-1-932159-73-8.
- ^ Yu, Mao-Hong; Ma, Guo-Wei; Qiang, Hong-Fu; Zhang, Yong-Qiang (2006). Generalized Plasticity. Springer. ISBN 3-540-25127-8.
- ^ Chen, Wai-Fah (2007). Plasticity in Reinforced Concrete. J. Ross Publishing. ISBN 978-1-932159-74-5.
- ^ Ziegenhain, Gerolf; and Urbassek, Herbert M.; "Reversible Plasticity in fcc metals" in Philosophical Magazine Letters, 89(11):717-723, 2009 DOI 10.1080/09500830903272900
- ^ Maaß, Robert; Derlet, Peter M. (January 2018). "Micro-plasticity and recent insights from intermittent and small-scale plasticity". Acta Materialia. 143: 338–363. arXiv:1704.07297. Bibcode:2018AcMat.143..338M. doi:10.1016/j.actamat.2017.06.023. S2CID 119387816.
- ^ Courtney, Thomas (2005). Mechanical Behavior of Materials (Second ed.). Long Grove, Illinois: Waveland Press, Inc. ISBN 978-1-57766-425-3.
- ^ Partridge, Peter (1969). Deformation and Fatigue of Hexagonal Close Packed Metals. University of Surrey.
{{cite book}}: CS1 maint: location missing publisher (link) - ^ Groves, Geoffrey W.; Kelly, Anthony (1963). "Independent Slip Systems in Crystals". Philosophical Magazine. 8 (89): 877–887. Bibcode:1963PMag....8..877G. doi:10.1080/14786436308213843.
- ^ Hill, Rodney (1998). The Mathematical Theory of Plasticity. Oxford University Press. ISBN 0-19-850367-9.
- ^ von Mises, Richard (1913). "Mechanik der festen Körper im plastisch-deformablen Zustand". Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen. Mathematisch-Physikalische Klasse. 1913 (1): 582–592.
- ^ Huber, Maksymilian Tytus (1904). "Właściwa praca odkształcenia jako miara wytezenia materiału". Czasopismo Techniczne. 22. Lwów. Translated as "Specific Work of Strain as a Measure of Material Effort". Archives of Mechanics. 56: 173–190. 2004.
- ^ See Timoshenko, Stephen P. (1953). History of Strength of Materials. New York: McGraw-Hill. p. 369. ISBN 9780486611877.
Further reading edit
- Ashby, Michael F. (2001). "Plastic Deformation of Cellular Materials". Encyclopedia of Materials: Science and Technology. Vol. 7. Oxford: Elsevier. pp. 7068–7071. ISBN 0-08-043152-6.
- Han, Weimin; Reddy, B. Daya (2013). Plasticity: Mathematical Theory and Numerical Analysis (2nd ed.). New York: Springer. ISBN 978-1-4614-5939-2.
- Kachanov, Lazar' Markovich (2004). Fundamentals of the Theory of Plasticity. Dover Books. ISBN 0-486-43583-0.
- Khan, Akhtar S.; Huang, Sujian (1995). Continuum Theory of Plasticity. Wiley. ISBN 0-471-31043-3.
- Simo, Juan C.; Hughes, Thomas J. R. (1998). Computational Inelasticity. Springer. ISBN 0-387-97520-9.
- Van Vliet, Krystyn J. (2006). "Mechanical Behavior of Materials". MIT Course Number 3.032. Massachusetts Institute of Technology.




