
Summary
In differential geometry, pushforward is a linear approximation of smooth maps (formulating manifold) on tangent spaces. Suppose that is a smooth map between smooth manifolds; then the differential of at a point , denoted , is, in some sense, the best linear approximation of near . It can be viewed as a generalization of the total derivative of ordinary calculus. Explicitly, the differential is a linear map from the tangent space of at to the tangent space of at , . Hence it can be used to push tangent vectors on forward to tangent vectors on . The differential of a map is also called, by various authors, the derivative or total derivative of .
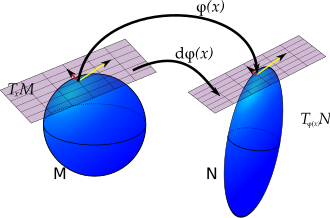
Motivation edit
Let be a smooth map from an open subset of to an open subset of . For any point in , the Jacobian of at (with respect to the standard coordinates) is the matrix representation of the total derivative of at , which is a linear map
between their tangent spaces. Note the tangent spaces are isomorphic to and , respectively. The pushforward generalizes this construction to the case that is a smooth function between any smooth manifolds and .
The differential of a smooth map edit
Let be a smooth map of smooth manifolds. Given the differential of at is a linear map
from the tangent space of at to the tangent space of at The image of a tangent vector under is sometimes called the pushforward of by The exact definition of this pushforward depends on the definition one uses for tangent vectors (for the various definitions see tangent space).
If tangent vectors are defined as equivalence classes of the curves for which then the differential is given by
Here, is a curve in with and is tangent vector to the curve at In other words, the pushforward of the tangent vector to the curve at is the tangent vector to the curve at
Alternatively, if tangent vectors are defined as derivations acting on smooth real-valued functions, then the differential is given by
for an arbitrary function and an arbitrary derivation at point (a derivation is defined as a linear map that satisfies the Leibniz rule, see: definition of tangent space via derivations). By definition, the pushforward of is in and therefore itself is a derivation, .
After choosing two charts around and around is locally determined by a smooth map between open sets of and , and
in the Einstein summation notation, where the partial derivatives are evaluated at the point in corresponding to in the given chart.
Extending by linearity gives the following matrix
Thus the differential is a linear transformation, between tangent spaces, associated to the smooth map at each point. Therefore, in some chosen local coordinates, it is represented by the Jacobian matrix of the corresponding smooth map from to . In general, the differential need not be invertible. However, if is a local diffeomorphism, then is invertible, and the inverse gives the pullback of
The differential is frequently expressed using a variety of other notations such as
It follows from the definition that the differential of a composite is the composite of the differentials (i.e., functorial behaviour). This is the chain rule for smooth maps.
Also, the differential of a local diffeomorphism is a linear isomorphism of tangent spaces.
The differential on the tangent bundle edit
The differential of a smooth map induces, in an obvious manner, a bundle map (in fact a vector bundle homomorphism) from the tangent bundle of to the tangent bundle of , denoted by , which fits into the following commutative diagram:
where and denote the bundle projections of the tangent bundles of and respectively.
induces a bundle map from to the pullback bundle φ∗TN over via
where and The latter map may in turn be viewed as a section of the vector bundle Hom(TM, φ∗TN) over M. The bundle map is also denoted by and called the tangent map. In this way, is a functor.
Pushforward of vector fields edit
Given a smooth map φ : M → N and a vector field X on M, it is not usually possible to identify a pushforward of X by φ with some vector field Y on N. For example, if the map φ is not surjective, there is no natural way to define such a pushforward outside of the image of φ. Also, if φ is not injective there may be more than one choice of pushforward at a given point. Nevertheless, one can make this difficulty precise, using the notion of a vector field along a map.
A section of φ∗TN over M is called a vector field along φ. For example, if M is a submanifold of N and φ is the inclusion, then a vector field along φ is just a section of the tangent bundle of N along M; in particular, a vector field on M defines such a section via the inclusion of TM inside TN. This idea generalizes to arbitrary smooth maps.
Suppose that X is a vector field on M, i.e., a section of TM. Then, yields, in the above sense, the pushforward φ∗X, which is a vector field along φ, i.e., a section of φ∗TN over M.
Any vector field Y on N defines a pullback section φ∗Y of φ∗TN with (φ∗Y)x = Yφ(x). A vector field X on M and a vector field Y on N are said to be φ-related if φ∗X = φ∗Y as vector fields along φ. In other words, for all x in M, dφx(X) = Yφ(x).
In some situations, given a X vector field on M, there is a unique vector field Y on N which is φ-related to X. This is true in particular when φ is a diffeomorphism. In this case, the pushforward defines a vector field Y on N, given by
A more general situation arises when φ is surjective (for example the bundle projection of a fiber bundle). Then a vector field X on M is said to be projectable if for all y in N, dφx(Xx) is independent of the choice of x in φ−1({y}). This is precisely the condition that guarantees that a pushforward of X, as a vector field on N, is well defined.
Examples edit
Pushforward from multiplication on Lie groups edit
Given a Lie group , we can use the multiplication map to get left multiplication and right multiplication maps . These maps can be used to construct left or right invariant vector fields on from its tangent space at the origin (which is its associated Lie algebra). For example, given we get an associated vector field on defined by
Pushforward for some Lie groups edit
For example, if is the Heisenberg group given by matrices
See also edit
References edit
- Lee, John M. (2003). Introduction to Smooth Manifolds. Springer Graduate Texts in Mathematics. Vol. 218.
- Jost, Jürgen (2002). Riemannian Geometry and Geometric Analysis. Berlin: Springer-Verlag. ISBN 3-540-42627-2. See section 1.6.
- Abraham, Ralph; Marsden, Jerrold E. (1978). Foundations of Mechanics. London: Benjamin-Cummings. ISBN 0-8053-0102-X. See section 1.7 and 2.3.










