Quarter_cubic_honeycomb Knowpia

Quarter cubic honeycomb

Type	Uniform honeycomb
Family	Truncated simplectic honeycomb Quarter hypercubic honeycomb
Indexing^[1]	J_25,33, A₁₃ W₁₀, G₆
Schläfli symbol	t_0,1{3^[4]} or q{4,3,4}
Coxeter-Dynkin diagram	= =
Cell types	{3,3} (3.6.6)
Face types	{3}, {6}
Vertex figure	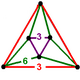(isosceles triangular antiprism)
Space group	Fd3m (227)
Coxeter group	${\tilde {A}}_{3}$ ×2₂, [[3^[4]]]
Dual	oblate cubille Cell: (1/4 of rhombic dodecahedron)
Properties	vertex-transitive, edge-transitive

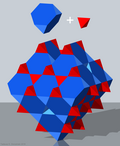
The quarter cubic honeycomb, quarter cubic cellulation or bitruncated alternated cubic honeycomb is a space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of tetrahedra and truncated tetrahedra in a ratio of 1:1. It is called "quarter-cubic" because its symmetry unit – the minimal block from which the pattern is developed by reflections – is four times that of the cubic honeycomb.

It is vertex-transitive with 6 truncated tetrahedra and 2 tetrahedra around each vertex.

A geometric honeycomb is a space-filling of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions.

Honeycombs are usually constructed in ordinary Euclidean ("flat") space, like the convex uniform honeycombs. They may also be constructed in non-Euclidean spaces, such as hyperbolic uniform honeycombs. Any finite uniform polytope can be projected to its circumsphere to form a uniform honeycomb in spherical space.

It is one of the 28 convex uniform honeycombs.

The faces of this honeycomb's cells form four families of parallel planes, each with a 3.6.3.6 tiling.

Its vertex figure is an isosceles antiprism: two equilateral triangles joined by six isosceles triangles.

John Horton Conway calls this honeycomb a truncated tetrahedrille, and its dual oblate cubille.

The vertices and edges represent a Kagome lattice in three dimensions,^[2] which is the pyrochlore lattice.

Construction edit

The quarter cubic honeycomb can be constructed in slab layers of truncated tetrahedra and tetrahedral cells, seen as two trihexagonal tilings. Two tetrahedra are stacked by a vertex and a central inversion. In each trihexagonal tiling, half of the triangles belong to tetrahedra, and half belong to truncated tetrahedra. These slab layers must be stacked with tetrahedra triangles to truncated tetrahedral triangles to construct the uniform quarter cubic honeycomb. Slab layers of hexagonal prisms and triangular prisms can be alternated for elongated honeycombs, but these are also not uniform.

	trihexagonal tiling:

Symmetry edit

Cells can be shown in two different symmetries. The reflection generated form represented by its Coxeter-Dynkin diagram has two colors of truncated cuboctahedra. The symmetry can be doubled by relating the pairs of ringed and unringed nodes of the Coxeter-Dynkin diagram, which can be shown with one colored tetrahedral and truncated tetrahedral cells.

Two uniform colorings
Symmetry	${\tilde {A}}_{3}$ , [3^[4]]	${\tilde {A}}_{3}$ ×2, [[3^[4]]]
Space group	F43m (216)	Fd3m (227)
Coloring
Vertex figure
Vertex figure symmetry	C_3v [3] (*33) order 6	D_3d [2⁺,6] (2*3) order 12

Related polyhedra edit

The subset of hexagonal faces of this honeycomb contains a regular skew apeirohedron {6,6\|3}.	Four sets of parallel planes of trihexagonal tilings exist throughout this honeycomb.

This honeycomb is one of five distinct uniform honeycombs^[3] constructed by the ${\tilde {A}}_{3}$ Coxeter group. The symmetry can be multiplied by the symmetry of rings in the Coxeter–Dynkin diagrams:

A3 honeycombs
Space group	Fibrifold	Square symmetry	Extended symmetry	Extended diagram	Extended group	Honeycomb diagrams
F43m (216)	1^o:2	a1	[3^[4]]		${\tilde {A}}_{3}$	(None)
Fm3m (225)	2⁻:2	d2	<[3^[4]]> ↔ [4,3^1,1]	↔	${\tilde {A}}_{3}$ ×2₁ ↔ ${\tilde {B}}_{3}$	₁, ₂
Fd3m (227)	2⁺:2	g2	[[3^[4]]] or [2⁺[3^[4]]]	↔	${\tilde {A}}_{3}$ ×2₂	_{3 Pm3m(221) 4−:2 d4}	<2[3^[4]]> ↔ [4,3,4]	↔	${\tilde {A}}_{3}$ ×4₁ ↔ ${\tilde {C}}_{3}$	₄
I3 (204)	8^−o	r8	[4[3^[4]]]⁺ ↔ [[4,3⁺,4]]	↔	½ ${\tilde {A}}_{3}$ ×8 ↔ ½ ${\tilde {C}}_{3}$ ×2	_(*)
Im3m (229)	8^o:2	r8	[4[3^[4]]] ↔ [[4,3,4]]	↔	${\tilde {A}}_{3}$ ×8 ↔ ${\tilde {C}}_{3}$ ×2	₅

C3 honeycombs
Space group	Fibrifold	Extended symmetry	Extended diagram	Order	Honeycombs
Pm3m (221)	4⁻:2	[4,3,4]		×1	₁, ₂, ₃, ₄, ₅, ₆
Fm3m (225)	2⁻:2	[1⁺,4,3,4] ↔ [4,3^1,1]	↔	Half	₇, ₁₁, ₁₂, ₁₃
I43m (217)	4^o:2	[[(4,3,4,2⁺)]]		Half × 2	₍₇₎,
Fd3m (227)	2⁺:2	[[1⁺,4,3,4,1⁺]] ↔ [[3^[4]]]	↔	Quarter × 2	₁₀,
Im3m (229)	8^o:2	[[4,3,4]]		×2	₍₁₎, ₈, ₉

The Quarter cubic honeycomb is related to a matrix of 3-dimensional honeycombs: q{2p,4,2q}

Euclidean/hyperbolic(paracompact/noncompact) quarter honeycombs q{p,3,q}
p \ q	4	6	8	... ∞
4	q{4,3,4} ↔ ↔	q{4,3,6} ↔ ↔	q{4,3,8} ↔	q{4,3,∞} ↔
6	q{6,3,4} ↔ ↔	q{6,3,6} ↔	q{6,3,8} ↔	q{6,3,∞} ↔
8	q{8,3,4} ↔	q{8,3,6} ↔	q{8,3,8} ↔	q{8,3,∞} ↔
... ∞	q{∞,3,4} ↔	q{∞,3,6} ↔	q{∞,3,8} ↔	q{∞,3,∞} ↔

References edit

^ For cross-referencing, they are given with list indices from Andreini (1-22), Williams(1-2,9-19), Johnson (11-19, 21-25, 31-34, 41-49, 51-52, 61-65), and Grünbaum(1-28).
^ "Physics Today article on the word kagome".
^ [1], OEIS sequence A000029 6-1 cases, skipping one with zero marks

John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, Architectonic and Catoptric tessellations, p 292-298, includes all the nonprismatic forms)
George Olshevsky, Uniform Panoploid Tetracombs, Manuscript (2006) (Complete list of 11 convex uniform tilings, 28 convex uniform honeycombs, and 143 convex uniform tetracombs)
Branko Grünbaum, Uniform tilings of 3-space. Geombinatorics 4(1994), 49 - 56.
Norman Johnson Uniform Polytopes, Manuscript (1991)
Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X.
Critchlow, Keith (1970). Order in Space: A design source book. Viking Press. ISBN 0-500-34033-1.
Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [2]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10] (1.9 Uniform space-fillings)
A. Andreini, Sulle reti di poliedri regolari e semiregolari e sulle corrispondenti reti correlative (On the regular and semiregular nets of polyhedra and on the corresponding correlative nets), Mem. Società Italiana della Scienze, Ser.3, 14 (1905) 75–129.
D. M. Y. Sommerville, An Introduction to the Geometry of n Dimensions. New York, E. P. Dutton, 1930. 196 pp. (Dover Publications edition, 1958) Chapter X: The Regular Polytopes
Klitzing, Richard. "3D Euclidean Honeycombs x3x3o3o3*a - batatoh - O27".
Uniform Honeycombs in 3-Space: 15-Batatoh

v t e Fundamental convex regular and uniform honeycombs in dimensions 2–9
Space	Family	${\tilde {A}}_{n-1}$	${\tilde {C}}_{n-1}$	${\tilde {B}}_{n-1}$	${\tilde {D}}_{n-1}$	${\tilde {G}}_{2}$ / ${\tilde {F}}_{4}$ / ${\tilde {E}}_{n-1}$
E²	Uniform tiling	{3^[3]}	δ₃	hδ₃	qδ₃	Hexagonal
E³	Uniform convex honeycomb	{3^[4]}	δ₄	hδ₄	qδ₄
E⁴	Uniform 4-honeycomb	{3^[5]}	δ₅	hδ₅	qδ₅	24-cell honeycomb
E⁵	Uniform 5-honeycomb	{3^[6]}	δ₆	hδ₆	qδ₆
E⁶	Uniform 6-honeycomb	{3^[7]}	δ₇	hδ₇	qδ₇	2₂₂
E⁷	Uniform 7-honeycomb	{3^[8]}	δ₈	hδ₈	qδ₈	1₃₃ • 3₃₁
E⁸	Uniform 8-honeycomb	{3^[9]}	δ₉	hδ₉	qδ₉	1₅₂ • 2₅₁ • 5₂₁
E⁹	Uniform 9-honeycomb	{3^[10]}	δ₁₀	hδ₁₀	qδ₁₀
E¹⁰	Uniform 10-honeycomb	{3^[11]}	δ₁₁	hδ₁₁	qδ₁₁
E^n-1	Uniform (n-1)-honeycomb	{3^[n]}	δ_n	hδ_n	qδ_n	1_k2 • 2_k1 • k₂₁

[1] For cross-referencing, they are given with list indices from Andreini (1-22), Williams(1-2,9-19), Johnson (11-19, 21-25, 31-34, 41-49, 51-52, 61-65), and Grünbaum(1-28).

[2] "Physics Today article on the word kagome".

[3] [1], OEIS sequence A000029 6-1 cases, skipping one with zero marks

[1]

[2]

[3]

Summary

Construction edit

Symmetry edit

Related polyhedra edit

See also edit

References edit