
Summary
In mathematics the regular paperfolding sequence, also known as the dragon curve sequence, is an infinite sequence of 0s and 1s. It is obtained from the repeating partial sequence
by filling in the question marks by another copy of the whole sequence. The first few terms of the resulting sequence are:
If a strip of paper is folded repeatedly in half in the same direction, times, it will get folds, whose direction (left or right) is given by the pattern of 0's and 1's in the first terms of the regular paperfolding sequence. Opening out each fold to create a right-angled corner (or, equivalently, making a sequence of left and right turns through a regular grid, following the pattern of the paperfolding sequence) produces a sequence of polygonal chains that approaches the dragon curve fractal:[1]

|
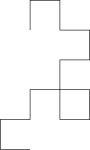
|
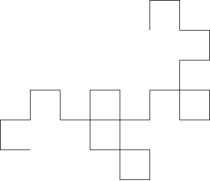
| ||
| 1 | 1 1 0 | 1 1 0 1 1 0 0 | 1 1 0 1 1 0 0 1 1 1 0 0 1 0 0 | ... |
Properties edit
The value of any given term in the regular paperfolding sequence, starting with , can be found recursively as follows. Divide by two, as many times as possible, to get a factorization of the form where is an odd number. Then
The paperfolding word 1101100111001001..., which is created by concatenating the terms of the regular paperfolding sequence, is a fixed point of the morphism or string substitution rules
- 11 → 1101
- 01 → 1001
- 10 → 1100
- 00 → 1000
as follows:
- 11 → 1101 → 11011001 → 1101100111001001 → 11011001110010011101100011001001 ...
It can be seen from the morphism rules that the paperfolding word contains at most three consecutive 0s and at most three consecutive 1s.
The paperfolding sequence also satisfies the symmetry relation:
which shows that the paperfolding word can be constructed as the limit of another iterated process as follows:
- 1
- 1 1 0
- 110 1 100
- 1101100 1 1100100
- 110110011100100 1 110110001100100
In each iteration of this process, a 1 is placed at the end of the previous iteration's string, then this string is repeated in reverse order, replacing 0 by 1 and vice versa.
Generating function edit
The generating function of the paperfolding sequence is given by
From the construction of the paperfolding sequence, it can be seen that G satisfies the functional relation
Paperfolding constant edit
Substituting x = 0.5 into the generating function gives a real number between 0 and 1 whose binary expansion is the paperfolding word
This number is known as the paperfolding constant[2] and has the value
General paperfolding sequence edit
The regular paperfolding sequence corresponds to folding a strip of paper consistently in the same direction. If we allow the direction of the fold to vary at each step we obtain a more general class of sequences. Given a binary sequence (fi), we can define a general paperfolding sequence with folding instructions (fi).
For a binary word w, let w‡ denote the reverse of the complement of w. Define an operator Fa as
and then define a sequence of words depending on the (fi) by w0 = ε,
The limit w of the sequence wn is a paperfolding sequence. The regular paperfolding sequence corresponds to the folding sequence fi = 1 for all i.
If n = m·2k where m is odd then
which may be used as a definition of a paperfolding sequence.[3]
Properties edit
References edit
- ^ Weisstein, Eric W. "Dragon Curve". MathWorld.
- ^ Weisstein, Eric W. "Paper Folding Constant". MathWorld.
- ^ a b Everest, Graham; van der Poorten, Alf; Shparlinski, Igor; Ward, Thomas (2003). Recurrence sequences. Mathematical Surveys and Monographs. Vol. 104. Providence, RI: American Mathematical Society. p. 235. ISBN 0-8218-3387-1. Zbl 1033.11006.
- Allouche, Jean-Paul; Shallit, Jeffrey (2003). Automatic Sequences: Theory, Applications, Generalizations. Cambridge University Press. ISBN 978-0-521-82332-6. Zbl 1086.11015.




