
Summary
| Rhombohedron | |
|---|---|
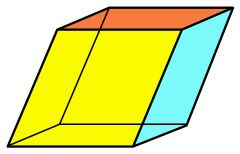
| |
| Type | prism |
| Faces | 6 rhombi |
| Edges | 12 |
| Vertices | 8 |
| Symmetry group | Ci , [2+,2+], (×), order 2 |
| Properties | convex, equilateral, zonohedron, parallelohedron |
In geometry, a rhombohedron (also called a rhombic hexahedron[1] or, inaccurately, a rhomboid) is a three-dimensional figure with six faces which are rhombi. It is a special case of a parallelepiped where all edges are the same length. It can be used to define the rhombohedral lattice system, a honeycomb with rhombohedral cells. A cube is a special case of a rhombohedron with all sides square.
In general a rhombohedron can have up to three types of rhombic faces in congruent opposite pairs, Ci symmetry, order 2.
Four points forming non-adjacent vertices of a rhombohedron necessarily form the four vertices of an orthocentric tetrahedron, and all orthocentric tetrahedra can be formed in this way.[2]
Rhombohedral lattice system edit
The rhombohedral lattice system has rhombohedral cells, with 6 congruent rhombic faces forming a trigonal trapezohedron:
Special cases by symmetry edit
| Form | Cube | Trigonal trapezohedron | Right rhombic prism | Oblique rhombic prism |
|---|---|---|---|---|
| Angle constraints |
||||
| Symmetry | Oh order 48 |
D3d order 12 |
D2h order 8 |
C2h order 4 |
| Faces | 6 squares | 6 congruent rhombi | 2 rhombi, 4 squares | 6 rhombi |
- Cube: with Oh symmetry, order 48. All faces are squares.
- Trigonal trapezohedron (also called isohedral rhombohedron):[3] with D3d symmetry, order 12. All non-obtuse internal angles of the faces are equal (all faces are congruent rhombi). This can be seen by stretching a cube on its body-diagonal axis. For example, a regular octahedron with two regular tetrahedra attached on opposite faces constructs a 60 degree trigonal trapezohedron.
- Right rhombic prism: with D2h symmetry, order 8. It is constructed by two rhombi and four squares. This can be seen by stretching a cube on its face-diagonal axis. For example, two right prisms with regular triangular bases attached together makes a 60 degree right rhombic prism.
- Oblique rhombic prism: with C2h symmetry, order 4. It has only one plane of symmetry, through four vertices, and six rhombic faces.
Solid geometry edit
For a unit (i.e.: with side length 1) isohedral rhombohedron,[3] with rhombic acute angle , with one vertex at the origin (0, 0, 0), and with one edge lying along the x-axis, the three generating vectors are
- e1 :
- e2 :
- e3 :
The other coordinates can be obtained from vector addition[4] of the 3 direction vectors: e1 + e2 , e1 + e3 , e2 + e3 , and e1 + e2 + e3 .
The volume of an isohedral rhombohedron, in terms of its side length and its rhombic acute angle , is a simplification of the volume of a parallelepiped, and is given by
We can express the volume another way :
As the area of the (rhombic) base is given by , and as the height of a rhombohedron is given by its volume divided by the area of its base, the height of an isohedral rhombohedron in terms of its side length and its rhombic acute angle is given by
Note:
- 3 , where 3 is the third coordinate of e3 .
The body diagonal between the acute-angled vertices is the longest. By rotational symmetry about that diagonal, the other three body diagonals, between the three pairs of opposite obtuse-angled vertices, are all the same length.
See also edit
References edit
- ^ "David Mitchell's Origami Heaven - Rhombic Polyhedra".
- ^ Court, N. A. (October 1934), "Notes on the orthocentric tetrahedron", American Mathematical Monthly, 41 (8): 499–502, doi:10.2307/2300415, JSTOR 2300415.
- ^ a b Lines, L (1965). Solid geometry: with chapters on space-lattices, sphere-packs and crystals. Dover Publications.
- ^ "Vector Addition". Wolfram. 17 May 2016. Retrieved 17 May 2016.
External links edit
- Weisstein, Eric W. "Rhombohedron". MathWorld.
- Volume Calculator https://rechneronline.de/pi/rhombohedron.php


