-
Kayakers surfing a standing wave in Great Falls Park
-
Mouth of the Carmel River - Standing waves are formed where the Carmel River meets the Pacific Ocean.

Summary
In physics, a standing wave, also known as a stationary wave, is a wave that oscillates in time but whose peak amplitude profile does not move in space. The peak amplitude of the wave oscillations at any point in space is constant with respect to time, and the oscillations at different points throughout the wave are in phase. The locations at which the absolute value of the amplitude is minimum are called nodes, and the locations where the absolute value of the amplitude is maximum are called antinodes.
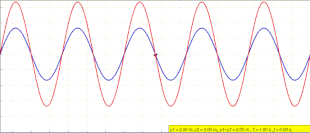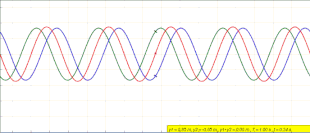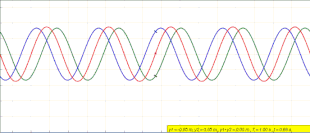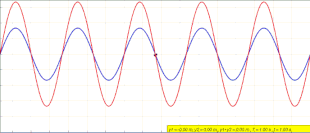
Standing waves were first described scientifically by Michael Faraday in 1831. Faraday observed standing waves on the surface of a liquid in a vibrating container.[1][2] Franz Melde coined the term "standing wave" (German: stehende Welle or Stehwelle) around 1860 and demonstrated the phenomenon in his classic experiment with vibrating strings.[3][4][5][6]
This phenomenon can occur because the medium is moving in the direction opposite to the movement of the wave, or it can arise in a stationary medium as a result of interference between two waves traveling in opposite directions. The most common cause of standing waves is the phenomenon of resonance, in which standing waves occur inside a resonator due to interference between waves reflected back and forth at the resonator's resonant frequency.
For waves of equal amplitude traveling in opposing directions, there is on average no net propagation of energy.
Moving medium edit
As an example of the first type, under certain meteorological conditions standing waves form in the atmosphere in the lee of mountain ranges. Such waves are often exploited by glider pilots.
Standing waves and hydraulic jumps also form on fast flowing river rapids and tidal currents such as the Saltstraumen maelstrom. A requirement for this in river currents is a flowing water with shallow depth in which the inertia of the water overcomes its gravity due to the supercritical flow speed (Froude number: 1.7 – 4.5, surpassing 4.5 results in direct standing wave[7]) and is therefore neither significantly slowed down by the obstacle nor pushed to the side. Many standing river waves are popular river surfing breaks.
Opposing waves edit
|
|
|
|
As an example of the second type, a standing wave in a transmission line is a wave in which the distribution of current, voltage, or field strength is formed by the superposition of two waves of the same frequency propagating in opposite directions. The effect is a series of nodes (zero displacement) and anti-nodes (maximum displacement) at fixed points along the transmission line. Such a standing wave may be formed when a wave is transmitted into one end of a transmission line and is reflected from the other end by an impedance mismatch, i.e., discontinuity, such as an open circuit or a short.[8] The failure of the line to transfer power at the standing wave frequency will usually result in attenuation distortion.
In practice, losses in the transmission line and other components mean that a perfect reflection and a pure standing wave are never achieved. The result is a partial standing wave, which is a superposition of a standing wave and a traveling wave. The degree to which the wave resembles either a pure standing wave or a pure traveling wave is measured by the standing wave ratio (SWR).[9]
Another example is standing waves in the open ocean formed by waves with the same wave period moving in opposite directions. These may form near storm centres, or from reflection of a swell at the shore, and are the source of microbaroms and microseisms.
Mathematical description edit
This section considers representative one- and two-dimensional cases of standing waves. First, an example of an infinite length string shows how identical waves traveling in opposite directions interfere to produce standing waves. Next, two finite length string examples with different boundary conditions demonstrate how the boundary conditions restrict the frequencies that can form standing waves. Next, the example of sound waves in a pipe demonstrates how the same principles can be applied to longitudinal waves with analogous boundary conditions.
Standing waves can also occur in two- or three-dimensional resonators. With standing waves on two-dimensional membranes such as drumheads, illustrated in the animations above, the nodes become nodal lines, lines on the surface at which there is no movement, that separate regions vibrating with opposite phase. These nodal line patterns are called Chladni figures. In three-dimensional resonators, such as musical instrument sound boxes and microwave cavity resonators, there are nodal surfaces. This section includes a two-dimensional standing wave example with a rectangular boundary to illustrate how to extend the concept to higher dimensions.
Standing wave on an infinite length string edit
To begin, consider a string of infinite length along the x-axis that is free to be stretched transversely in the y direction.
For a harmonic wave traveling to the right along the string, the string's displacement in the y direction as a function of position x and time t is[10]
The displacement in the y-direction for an identical harmonic wave traveling to the left is
where
- ymax is the amplitude of the displacement of the string for each wave,
- ω is the angular frequency or equivalently 2π times the frequency f,
- λ is the wavelength of the wave.
For identical right- and left-traveling waves on the same string, the total displacement of the string is the sum of yR and yL,
Using the trigonometric sum-to-product identity ,
-
(1)
Equation (1) does not describe a traveling wave. At any position x, y(x,t) simply oscillates in time with an amplitude that varies in the x-direction as .[10] The animation at the beginning of this article depicts what is happening. As the left-traveling blue wave and right-traveling green wave interfere, they form the standing red wave that does not travel and instead oscillates in place.
Because the string is of infinite length, it has no boundary condition for its displacement at any point along the x-axis. As a result, a standing wave can form at any frequency.
At locations on the x-axis that are even multiples of a quarter wavelength,
the amplitude is always zero. These locations are called nodes. At locations on the x-axis that are odd multiples of a quarter wavelength
the amplitude is maximal, with a value of twice the amplitude of the right- and left-traveling waves that interfere to produce this standing wave pattern. These locations are called anti-nodes. The distance between two consecutive nodes or anti-nodes is half the wavelength, λ/2.
Standing wave on a string with two fixed ends edit
Next, consider a string with fixed ends at x = 0 and x = L. The string will have some damping as it is stretched by traveling waves, but assume the damping is very small. Suppose that at the x = 0 fixed end a sinusoidal force is applied that drives the string up and down in the y-direction with a small amplitude at some frequency f. In this situation, the driving force produces a right-traveling wave. That wave reflects off the right fixed end and travels back to the left, reflects again off the left fixed end and travels back to the right, and so on. Eventually, a steady state is reached where the string has identical right- and left-traveling waves as in the infinite-length case and the power dissipated by damping in the string equals the power supplied by the driving force so the waves have constant amplitude.
Equation (1) still describes the standing wave pattern that can form on this string, but now Equation (1) is subject to boundary conditions where y = 0 at x = 0 and x = L because the string is fixed at x = L and because we assume the driving force at the fixed x = 0 end has small amplitude. Checking the values of y at the two ends,
This boundary condition is in the form of the Sturm–Liouville formulation. The latter boundary condition is satisfied when . L is given, so the boundary condition restricts the wavelength of the standing waves to[11]
-
(2)
Waves can only form standing waves on this string if they have a wavelength that satisfies this relationship with L. If waves travel with speed v along the string, then equivalently the frequency of the standing waves is restricted to[11][12]
The standing wave with n = 1 oscillates at the fundamental frequency and has a wavelength that is twice the length of the string. Higher integer values of n correspond to modes of oscillation called harmonics or overtones. Any standing wave on the string will have n + 1 nodes including the fixed ends and n anti-nodes.
To compare this example's nodes to the description of nodes for standing waves in the infinite length string, Equation (2) can be rewritten as
In this variation of the expression for the wavelength, n must be even. Cross multiplying we see that because L is a node, it is an even multiple of a quarter wavelength,
This example demonstrates a type of resonance and the frequencies that produce standing waves can be referred to as resonant frequencies.[11][13][14]
Standing wave on a string with one fixed end edit
Next, consider the same string of length L, but this time it is only fixed at x = 0. At x = L, the string is free to move in the y direction. For example, the string might be tied at x = L to a ring that can slide freely up and down a pole. The string again has small damping and is driven by a small driving force at x = 0.
In this case, Equation (1) still describes the standing wave pattern that can form on the string, and the string has the same boundary condition of y = 0 at x = 0. However, at x = L where the string can move freely there should be an anti-node with maximal amplitude of y. Equivalently, this boundary condition of the "free end" can be stated as ∂y/∂x = 0 at x = L, which is in the form of the Sturm–Liouville formulation. The intuition for this boundary condition ∂y/∂x = 0 at x = L is that the motion of the "free end" will follow that of the point to its left.
Reviewing Equation (1), for x = L the largest amplitude of y occurs when ∂y/∂x = 0, or
This leads to a different set of wavelengths than in the two-fixed-ends example. Here, the wavelength of the standing waves is restricted to
Equivalently, the frequency is restricted to
In this example n only takes odd values. Because L is an anti-node, it is an odd multiple of a quarter wavelength. Thus the fundamental mode in this example only has one quarter of a complete sine cycle–zero at x = 0 and the first peak at x = L–the first harmonic has three quarters of a complete sine cycle, and so on.
This example also demonstrates a type of resonance and the frequencies that produce standing waves are called resonant frequencies.
Standing wave in a pipe edit
Consider a standing wave in a pipe of length L. The air inside the pipe serves as the medium for longitudinal sound waves traveling to the right or left through the pipe. While the transverse waves on the string from the previous examples vary in their displacement perpendicular to the direction of wave motion, the waves traveling through the air in the pipe vary in terms of their pressure and longitudinal displacement along the direction of wave motion. The wave propagates by alternately compressing and expanding air in segments of the pipe, which displaces the air slightly from its rest position and transfers energy to neighboring segments through the forces exerted by the alternating high and low air pressures.[15] Equations resembling those for the wave on a string can be written for the change in pressure Δp due to a right- or left-traveling wave in the pipe.
where
- pmax is the pressure amplitude or the maximum increase or decrease in air pressure due to each wave,
- ω is the angular frequency or equivalently 2π times the frequency f,
- λ is the wavelength of the wave.
If identical right- and left-traveling waves travel through the pipe, the resulting superposition is described by the sum
This formula for the pressure is of the same form as Equation (1), so a stationary pressure wave forms that is fixed in space and oscillates in time.
If the end of a pipe is closed, the pressure is maximal since the closed end of the pipe exerts a force that restricts the movement of air. This corresponds to a pressure anti-node (which is a node for molecular motions, because the molecules near the closed end can't move). If the end of the pipe is open, the pressure variations are very small, corresponding to a pressure node (which is an anti-node for molecular motions, because the molecules near the open end can move freely).[16][17] The exact location of the pressure node at an open end is actually slightly beyond the open end of the pipe, so the effective length of the pipe for the purpose of determining resonant frequencies is slightly longer than its physical length.[18] This difference in length is ignored in this example. In terms of reflections, open ends partially reflect waves back into the pipe, allowing some energy to be released into the outside air. Ideally, closed ends reflect the entire wave back in the other direction.[18][19]
First consider a pipe that is open at both ends, for example an open organ pipe or a recorder. Given that the pressure must be zero at both open ends, the boundary conditions are analogous to the string with two fixed ends,
which only occurs when the wavelength of standing waves is[18]
or equivalently when the frequency is[18][20]
where v is the speed of sound.
Next, consider a pipe that is open at x = 0 (and therefore has a pressure node) and closed at x = L (and therefore has a pressure anti-node). The closed "free end" boundary condition for the pressure at x = L can be stated as ∂(Δp)/∂x = 0, which is in the form of the Sturm–Liouville formulation. The intuition for this boundary condition ∂(Δp)/∂x = 0 at x = L is that the pressure of the closed end will follow that of the point to its left. Examples of this setup include a bottle and a clarinet. This pipe has boundary conditions analogous to the string with only one fixed end. Its standing waves have wavelengths restricted to[18]
or equivalently the frequency of standing waves is restricted to[21][20]
For the case where one end is closed, n only takes odd values just like in the case of the string fixed at only one end.
So far, the wave has been written in terms of its pressure as a function of position x and time. Alternatively, the wave can be written in terms of its longitudinal displacement of air, where air in a segment of the pipe moves back and forth slightly in the x-direction as the pressure varies and waves travel in either or both directions. The change in pressure Δp and longitudinal displacement s are related as[22]
where ρ is the density of the air. In terms of longitudinal displacement, closed ends of pipes correspond to nodes since air movement is restricted and open ends correspond to anti-nodes since the air is free to move.[18][23] A similar, easier to visualize phenomenon occurs in longitudinal waves propagating along a spring.[24]
We can also consider a pipe that is closed at both ends. In this case, both ends will be pressure anti-nodes or equivalently both ends will be displacement nodes. This example is analogous to the case where both ends are open, except the standing wave pattern has a π⁄2 phase shift along the x-direction to shift the location of the nodes and anti-nodes. For example, the longest wavelength that resonates–the fundamental mode–is again twice the length of the pipe, except that the ends of the pipe have pressure anti-nodes instead of pressure nodes. Between the ends there is one pressure node. In the case of two closed ends, the wavelength is again restricted to
and the frequency is again restricted to
A Rubens tube provides a way to visualize the pressure variations of the standing waves in a tube with two closed ends.[25]
2D standing wave with a rectangular boundary edit
Next, consider transverse waves that can move along a two dimensional surface within a rectangular boundary of length Lx in the x-direction and length Ly in the y-direction. Examples of this type of wave are water waves in a pool or waves on a rectangular sheet that has been pulled taut. The waves displace the surface in the z-direction, with z = 0 defined as the height of the surface when it is still.
In two dimensions and Cartesian coordinates, the wave equation is
where
- z(x,y,t) is the displacement of the surface,
- c is the speed of the wave.
To solve this differential equation, let's first solve for its Fourier transform, with
Taking the Fourier transform of the wave equation,
This is an eigenvalue problem where the frequencies correspond to eigenvalues that then correspond to frequency-specific modes or eigenfunctions. Specifically, this is a form of the Helmholtz equation and it can be solved using separation of variables.[26] Assume
Dividing the Helmholtz equation by Z,
This leads to two coupled ordinary differential equations. The x term equals a constant with respect to x that we can define as
Solving for X(x),
This x-dependence is sinusoidal–recalling Euler's formula–with constants Akx and Bkx determined by the boundary conditions. Likewise, the y term equals a constant with respect to y that we can define as
and the dispersion relation for this wave is therefore
Solving the differential equation for the y term,
Multiplying these functions together and applying the inverse Fourier transform, z(x,y,t) is a superposition of modes where each mode is the product of sinusoidal functions for x, y, and t,
The constants that determine the exact sinusoidal functions depend on the boundary conditions and initial conditions. To see how the boundary conditions apply, consider an example like the sheet that has been pulled taut where z(x,y,t) must be zero all around the rectangular boundary. For the x dependence, z(x,y,t) must vary in a way that it can be zero at both x = 0 and x = Lx for all values of y and t. As in the one dimensional example of the string fixed at both ends, the sinusoidal function that satisfies this boundary condition is
with kx restricted to
Likewise, the y dependence of z(x,y,t) must be zero at both y = 0 and y = Ly, which is satisfied by
Restricting the wave numbers to these values also restricts the frequencies that resonate to
If the initial conditions for z(x,y,0) and its time derivative ż(x,y,0) are chosen so the t-dependence is a cosine function, then standing waves for this system take the form
So, standing waves inside this fixed rectangular boundary oscillate in time at certain resonant frequencies parameterized by the integers n and m. As they oscillate in time, they do not travel and their spatial variation is sinusoidal in both the x- and y-directions such that they satisfy the boundary conditions. The fundamental mode, n = 1 and m = 1, has a single antinode in the middle of the rectangle. Varying n and m gives complicated but predictable two-dimensional patterns of nodes and antinodes inside the rectangle.[27]
From the dispersion relation, in certain situations different modes–meaning different combinations of n and m–may resonate at the same frequency even though they have different shapes for their x- and y-dependence. For example, if the boundary is square, Lx = Ly, the modes n = 1 and m = 7, n = 7 and m = 1, and n = 5 and m = 5 all resonate at
Recalling that ω determines the eigenvalue in the Helmholtz equation above, the number of modes corresponding to each frequency relates to the frequency's multiplicity as an eigenvalue.
Standing wave ratio, phase, and energy transfer edit
If the two oppositely moving traveling waves are not of the same amplitude, they will not cancel completely at the nodes, the points where the waves are 180° out of phase, so the amplitude of the standing wave will not be zero at the nodes, but merely a minimum. Standing wave ratio (SWR) is the ratio of the amplitude at the antinode (maximum) to the amplitude at the node (minimum). A pure standing wave will have an infinite SWR. It will also have a constant phase at any point in space (but it may undergo a 180° inversion every half cycle). A finite, non-zero SWR indicates a wave that is partially stationary and partially travelling. Such waves can be decomposed into a superposition of two waves: a travelling wave component and a stationary wave component. An SWR of one indicates that the wave does not have a stationary component – it is purely a travelling wave, since the ratio of amplitudes is equal to 1.[28]
A pure standing wave does not transfer energy from the source to the destination.[29] However, the wave is still subject to losses in the medium. Such losses will manifest as a finite SWR, indicating a travelling wave component leaving the source to supply the losses. Even though the SWR is now finite, it may still be the case that no energy reaches the destination because the travelling component is purely supplying the losses. However, in a lossless medium, a finite SWR implies a definite transfer of energy to the destination.
Examples edit
One easy example to understand standing waves is two people shaking either end of a jump rope. If they shake in sync the rope can form a regular pattern of waves oscillating up and down, with stationary points along the rope where the rope is almost still (nodes) and points where the arc of the rope is maximum (antinodes).
Acoustic resonance edit
Standing waves are also observed in physical media such as strings and columns of air. Any waves traveling along the medium will reflect back when they reach the end. This effect is most noticeable in musical instruments where, at various multiples of a vibrating string or air column's natural frequency, a standing wave is created, allowing harmonics to be identified. Nodes occur at fixed ends and anti-nodes at open ends. If fixed at only one end, only odd-numbered harmonics are available. At the open end of a pipe the anti-node will not be exactly at the end as it is altered by its contact with the air and so end correction is used to place it exactly. The density of a string will affect the frequency at which harmonics will be produced; the greater the density the lower the frequency needs to be to produce a standing wave of the same harmonic.
Visible light edit
Standing waves are also observed in optical media such as optical waveguides and optical cavities. Lasers use optical cavities in the form of a pair of facing mirrors, which constitute a Fabry–Pérot interferometer. The gain medium in the cavity (such as a crystal) emits light coherently, exciting standing waves of light in the cavity.[32] The wavelength of light is very short (in the range of nanometers, 10−9 m) so the standing waves are microscopic in size. One use for standing light waves is to measure small distances, using optical flats.
X-rays edit
Interference between X-ray beams can form an X-ray standing wave (XSW) field.[33] Because of the short wavelength of X-rays (less than 1 nanometer), this phenomenon can be exploited for measuring atomic-scale events at material surfaces. The XSW is generated in the region where an X-ray beam interferes with a diffracted beam from a nearly perfect single crystal surface or a reflection from an X-ray mirror. By tuning the crystal geometry or X-ray wavelength, the XSW can be translated in space, causing a shift in the X-ray fluorescence or photoelectron yield from the atoms near the surface. This shift can be analyzed to pinpoint the location of a particular atomic species relative to the underlying crystal structure or mirror surface. The XSW method has been used to clarify the atomic-scale details of dopants in semiconductors,[34] atomic and molecular adsorption on surfaces,[35] and chemical transformations involved in catalysis.[36]
Mechanical waves edit
Standing waves can be mechanically induced into a solid medium using resonance. One easy to understand example is two people shaking either end of a jump rope. If they shake in sync, the rope will form a regular pattern with nodes and antinodes and appear to be stationary, hence the name standing wave. Similarly a cantilever beam can have a standing wave imposed on it by applying a base excitation. In this case the free end moves the greatest distance laterally compared to any location along the beam. Such a device can be used as a sensor to track changes in frequency or phase of the resonance of the fiber. One application is as a measurement device for dimensional metrology.[37][38]
Seismic waves edit
Standing surface waves on the Earth are observed as free oscillations of the Earth.
Faraday waves edit
The Faraday wave is a non-linear standing wave at the air-liquid interface induced by hydrodynamic instability. It can be used as a liquid-based template to assemble microscale materials.[39]
Seiches edit
A seiche is an example of a standing wave in an enclosed body of water. It is characterised by the oscillatory behaviour of the water level at either end of the body and typically has a nodal point near the middle of the body where very little change in water level is observed. It should be distinguished from a simple storm surge where no oscillation is present. In sizeable lakes, the period of such oscillations may be between minutes and hours, for example Lake Geneva's longitudinal period is 73 minutes and its transversal seiche has a period of around 10 minutes,[40] while Lake Huron can be seen to have resonances with periods between 1 and 2 hours.[41] See Lake seiches.[42][43][44]
See also edit
Waves edit
Electronics edit
Notes edit
- ^ Alwyn Scott (ed), Encyclopedia of Nonlinear Science, p. 683, Routledge, 2006 ISBN 1135455589.
- ^ Theodore Y. Wu, "Stability of nonlinear waves resonantly sustained", Nonlinear Instability of Nonparallel Flows: IUTAM Symposium Potsdam, New York, p. 368, Springer, 2012 ISBN 3642850847.
- ^ Melde, Franz. Ueber einige krumme Flächen, welche von Ebenen, parallel einer bestimmten Ebene, durchschnitten, als Durchschnittsfigur einen Kegelschnitt liefern: Inaugural-Dissertation... Koch, 1859.
- ^ Melde, Franz. "Ueber die Erregung stehender Wellen eines fadenförmigen Körpers." Annalen der Physik 185, no. 2 (1860): 193–215.
- ^ Melde, Franz. Die Lehre von den Schwingungscurven...: mit einem Atlas von 11 Tafeln in Steindruck. JA Barth, 1864.
- ^ Melde, Franz. "Akustische Experimentaluntersuchungen." Annalen der Physik 257, no. 3 (1884): 452–470.
- ^ Dietsche, Daniela (2014-12-31). "Surfbare Wechselsprünge | Espazium". www.espazium.ch (in German). Retrieved 2022-01-13.
- ^ This article incorporates public domain material from Federal Standard 1037C. General Services Administration. Archived from the original on 2022-01-22.
- ^ Blackstock, David T. (2000), Fundamentals of Physical Acoustics, Wiley–IEEE, p. 141, ISBN 0-471-31979-1
- ^ a b Halliday, Resnick & Walker 2005, p. 432.
- ^ a b c Halliday, Resnick & Walker 2005, p. 434.
- ^ Serway & Faughn 1992, p. 472.
- ^ Serway & Faughn 1992, p. 475-476.
- ^ String Resonance. Digital Sound & Music. May 21, 2014. YouTube Video ID: oZ38Y0K8e-Y. Retrieved August 22, 2020.
- ^ Halliday, Resnick & Walker 2005, p. 450.
- ^ Nave, C. R. (2016). "Standing Waves". HyperPhysics. Georgia State University. Retrieved August 23, 2020.
- ^ Streets 2010, p. 6.
- ^ a b c d e f Halliday, Resnick & Walker 2005, p. 457.
- ^ Streets 2010, p. 15.
- ^ a b Serway & Faughn 1992, p. 478.
- ^ Halliday, Resnick & Walker 2005, p. 458.
- ^ Halliday, Resnick & Walker 2005, p. 451.
- ^ Serway & Faughn 1992, p. 477.
- ^ Thomas-Palmer, Jonathan (October 16, 2019). Longitudinal Standing Waves Demonstration. Flipping Physics. Event occurs at 4:11. YouTube video ID: 3QbmvunlQR0. Retrieved August 23, 2020.
- ^ Mould, Steve (April 13, 2017). A better description of resonance. YouTube. Event occurs at 6:04. YouTube video ID: dihQuwrf9yQ. Retrieved August 23, 2020.
- ^ Weisstein, Eric W. "Helmholtz Differential Equation--Cartesian Coordinates". MathWorld--A Wolfram Web Resource. Retrieved January 2, 2021.
- ^ Gallis, Michael R. (February 15, 2008). 2D Standing Wave Patterns (rectangular fixed boundaries). Animations for Physics and Astronomy. Pennsylvania State University. Also available as YouTube Video ID: NMlys8A0_4s. Retrieved December 28, 2020.
- ^ R S Rao, Microwave Engineering, pp. 153–154, PHI Learning, 2015 ISBN 8120351592.
- ^ K A Tsokos, Physics for the IB Diploma, p. 251, Cambridge University Press, 2010 ISBN 0521138213.
- ^ A Wave Dynamical Interpretation of Saturn's Polar Region Archived 2011-10-21 at the Wayback Machine, M. Allison, D. A. Godfrey, R. F. Beebe, Science vol. 247, pg. 1061 (1990)
- ^ Barbosa Aguiar, Ana C. (2010). "A laboratory model of Saturn's North Polar Hexagon". Icarus. 206 (2): 755–763. Bibcode:2010Icar..206..755B. doi:10.1016/j.icarus.2009.10.022.
- ^ Pedrotti, Frank L.; Pedrotti, Leno M. (2017). Introduction to Optics (3 ed.). Cambridge University Press. ISBN 978-1-108-42826-2.
- ^ Batterman, Boris W.; Cole, Henderson (1964). "Dynamical Diffraction of X Rays by Perfect Crystals". Reviews of Modern Physics. 36 (3): 681–717. Bibcode:1964RvMP...36..681B. doi:10.1103/RevModPhys.36.681.
- ^ Batterman, Boris W. (1969). "Detection of Foreign Atom Sites by Their X-Ray Fluorescence Scattering". Physical Review Letters. 22 (14): 703–705. Bibcode:1969PhRvL..22..703B. doi:10.1103/PhysRevLett.22.703.
- ^ Golovchenko, J. A.; Patel, J. R.; Kaplan, D. R.; Cowan, P. L.; Bedzyk, M. J. (1982). "Solution to the Surface Registration Problem Using X-Ray Standing Waves" (PDF). Physical Review Letters. 49 (8): 560–563. Bibcode:1982PhRvL..49..560G. doi:10.1103/PhysRevLett.49.560.
- ^ Feng, Z.; Kim, C.-Y.; Elam, J.W.; Ma, Q.; Zhang, Z.; Bedzyk, M.J. (2009). "Direct Atomic-Scale Observation of Redox-Induced Cation Dynamics in an Oxide-Supported Monolayer Catalyst: WOx/α-Fe2O3(0001)". J. Am. Chem. Soc. 131 (51): 18200–18201. doi:10.1021/ja906816y. PMID 20028144.
- ^ Bauza, Marcin B.; Hocken, Robert J.; Smith, Stuart T.; Woody, Shane C. (2005). "Development of a virtual probe tip with an application to high aspect ratio microscale features". Review of Scientific Instruments. 76 (9): 095112–095112–8. Bibcode:2005RScI...76i5112B. doi:10.1063/1.2052027.
- ^ "Precision Engineering and Manufacturing Solutions – IST Precision". www.insitutec.com. Archived from the original on 31 July 2016. Retrieved 28 April 2018.
- ^ Chen, Pu (2014). "Microscale Assembly Directed by Liquid-Based Template". Advanced Materials. 26 (34): 5936–5941. doi:10.1002/adma.201402079. PMC 4159433. PMID 24956442.
- ^ Lemmin, Ulrich (2012), "Surface Seiches", in Bengtsson, Lars; Herschy, Reginald W.; Fairbridge, Rhodes W. (eds.), Encyclopedia of Lakes and Reservoirs, Encyclopedia of Earth Sciences Series, Springer Netherlands, pp. 751–753, doi:10.1007/978-1-4020-4410-6_226, ISBN 978-1-4020-4410-6
- ^ "Lake Huron Storm Surge July 13, 1995". NOAA. Archived from the original on 2008-09-16. Retrieved 2023-01-01.
- ^ Korgen, Ben (February 2000). "Bonanza for Lake Superior: Seiches Do More Than Move Water". seagrant.umn.edu. University of Minnesota Duluth. Archived from the original on 2007-12-27.
- ^ "Seiche". www.soest.hawaii.edu. Archived from the original on 2019-01-26. Retrieved 2023-01-01.
- ^ Johnson, Scott K. (30 June 2013). "Japanese earthquake literally made waves in Norway". Ars Technica. Archived from the original on 30 July 2022. Retrieved 2023-01-01.
References edit
- Halliday, David; Resnick, Robert; Walker, Jearl (2005). Fundamentals of Physics (7th ed.). John Wiley & Sons. ISBN 0-471-42959-7.
- Serway, Raymond A.; Faughn, Jerry S. (1992). College Physics (3rd ed.). Saunders College Publishing. ISBN 0-03-076377-0.
- Streets, J. (2010). "Chapter 16 – Superposition and Standing Waves" (PDF). Department of Physics. PHYS122 Fundamentals of Physics II. University of Maryland. Retrieved August 23, 2020.
External links edit
- Media related to Standing waves at Wikimedia Commons


