
Summary
In mathematics, subderivatives (or subgradient) generalizes the derivative to convex functions which are not necessarily differentiable. The set of subderivatives at a point is called the subdifferential at that point.[1] Subderivatives arise in convex analysis, the study of convex functions, often in connection to convex optimization.
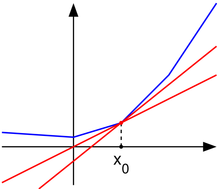
Let be a real-valued convex function defined on an open interval of the real line. Such a function need not be differentiable at all points: For example, the absolute value function is non-differentiable when . However, as seen in the graph on the right (where in blue has non-differentiable kinks similar to the absolute value function), for any in the domain of the function one can draw a line which goes through the point and which is everywhere either touching or below the graph of f. The slope of such a line is called a subderivative.
Definition edit
Rigorously, a subderivative of a convex function at a point in the open interval is a real number such that
Example edit
Consider the function which is convex. Then, the subdifferential at the origin is the interval . The subdifferential at any point is the singleton set , while the subdifferential at any point is the singleton set . This is similar to the sign function, but is not single-valued at , instead including all possible subderivatives.
Properties edit
- A convex function is differentiable at if and only if the subdifferential is a singleton set, which is .
- A point is a global minimum of a convex function if and only if zero is contained in the subdifferential. For instance, in the figure above, one may draw a horizontal "subtangent line" to the graph of at . This last property is a generalization of the fact that the derivative of a function differentiable at a local minimum is zero.
- If and are convex functions with subdifferentials and with being the interior point of one of the functions, then the subdifferential of is (where the addition operator denotes the Minkowski sum). This reads as "the subdifferential of a sum is the sum of the subdifferentials."[3]
The subgradient edit
The concepts of subderivative and subdifferential can be generalized to functions of several variables. If is a real-valued convex function defined on a convex open set in the Euclidean space , a vector in that space is called a subgradient at if for any one has that
where the dot denotes the dot product. The set of all subgradients at is called the subdifferential at and is denoted . The subdifferential is always a nonempty convex compact set.
These concepts generalize further to convex functions on a convex set in a locally convex space . A functional in the dual space is called the subgradient at in if for all ,
The set of all subgradients at is called the subdifferential at and is again denoted . The subdifferential is always a convex closed set. It can be an empty set; consider for example an unbounded operator, which is convex, but has no subgradient. If is continuous, the subdifferential is nonempty.
History edit
The subdifferential on convex functions was introduced by Jean Jacques Moreau and R. Tyrrell Rockafellar in the early 1960s. The generalized subdifferential for nonconvex functions was introduced by F.H. Clarke and R.T. Rockafellar in the early 1980s.[4]
See also edit
References edit
- ^ Bubeck, S. (2014). Theory of Convex Optimization for Machine Learning. ArXiv, abs/1405.4980.
- ^ Rockafellar, R. T. (1970). Convex Analysis. Princeton University Press. p. 242 [Theorem 25.1]. ISBN 0-691-08069-0.
- ^ Lemaréchal, Claude; Hiriart-Urruty, Jean-Baptiste (2001). Fundamentals of Convex Analysis. Springer-Verlag Berlin Heidelberg. p. 183. ISBN 978-3-642-56468-0.
- ^ Clarke, Frank H. (1983). Optimization and nonsmooth analysis. New York: John Wiley & Sons. pp. xiii+308. ISBN 0-471-87504-X. MR 0709590.
- Borwein, Jonathan; Lewis, Adrian S. (2010). Convex Analysis and Nonlinear Optimization : Theory and Examples (2nd ed.). New York: Springer. ISBN 978-0-387-31256-9.
- Hiriart-Urruty, Jean-Baptiste; Lemaréchal, Claude (2001). Fundamentals of Convex Analysis. Springer. ISBN 3-540-42205-6.
- Zălinescu, C. (2002). Convex analysis in general vector spaces. World Scientific Publishing Co., Inc. pp. xx+367. ISBN 981-238-067-1. MR 1921556.
External links edit
- "Uses of ". Stack Exchange. September 18, 2011.








