Supporting_hyperplane Knowpia

In geometry, a supporting hyperplane of a set $S$ in Euclidean space $\mathbb {R} ^{n}$ is a hyperplane that has both of the following two properties:^[1]

$S$ is entirely contained in one of the two closed half-spaces bounded by the hyperplane,
$S$ has at least one boundary-point on the hyperplane.

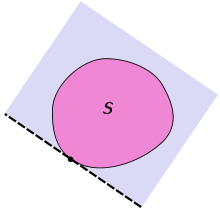
Here, a closed half-space is the half-space that includes the points within the hyperplane.

Supporting hyperplane theorem edit

A convex set can have more than one supporting hyperplane at a given point on its boundary.

This theorem states that if $S$ is a convex set in the topological vector space $X=\mathbb {R} ^{n},$ and $x_{0}$ is a point on the boundary of $S,$ then there exists a supporting hyperplane containing $x_{0}.$ If $x^{*}\in X^{*}\backslash \{0\}$ ( $X^{*}$ is the dual space of $X$ , $x^{*}$ is a nonzero linear functional) such that $x^{*}\left(x_{0}\right)\geq x^{*}(x)$ for all $x\in S$ , then

H=\{x\in X:x^{*}(x)=x^{*}\left(x_{0}\right)\}

defines a supporting hyperplane.^[2]

Conversely, if $S$ is a closed set with nonempty interior such that every point on the boundary has a supporting hyperplane, then $S$ is a convex set, and is the intersection of all its supporting closed half-spaces.^[2]

The hyperplane in the theorem may not be unique, as noticed in the second picture on the right. If the closed set $S$ is not convex, the statement of the theorem is not true at all points on the boundary of $S,$ as illustrated in the third picture on the right.

The supporting hyperplanes of convex sets are also called tac-planes or tac-hyperplanes.^[3]

The forward direction can be proved as a special case of the separating hyperplane theorem (see the page for the proof). For the converse direction,

Proof

Define $T$ to be the intersection of all its supporting closed half-spaces. Clearly $S\subset T$ . Now let $y\not \in S$ , show $y\not \in T$ .

Let $x\in \mathrm {int} (S)$ , and consider the line segment $[x,y]$ . Let $t$ be the largest number such that $[x,t(y-x)+x]$ is contained in $S$ . Then $t\in (0,1)$ .

Let $b=t(y-x)+x$ , then $b\in \partial S$ . Draw a supporting hyperplane across $b$ . Let it be represented as a nonzero linear functional $f:\mathbb {R} ^{n}\to \mathbb {R}$ such that $\forall a\in S,f(a)\geq f(b)$ . Then since $x\in \mathrm {int} (S)$ , we have $f(x)>f(b)$ . Thus by ${\frac {f(y)-f(b)}{1-t}}={\frac {f(b)-f(x)}{t}}$ , we have $f(y)<f(b)$ , so $y\not \in T$ .

Notes edit

^ Luenberger, David G. (1969). Optimization by Vector Space Methods. New York: John Wiley & Sons. p. 133. ISBN 978-0-471-18117-0.
^ ^a ^b Boyd, Stephen P.; Vandenberghe, Lieven (2004). Convex Optimization (pdf). Cambridge University Press. pp. 50–51. ISBN 978-0-521-83378-3. Retrieved October 15, 2011.
^ Cassels, John W. S. (1997), An Introduction to the Geometry of Numbers, Springer Classics in Mathematics (reprint of 1959[3] and 1971 Springer-Verlag ed.), Springer-Verlag.

References & further reading edit

Ostaszewski, Adam (1990). Advanced mathematical methods. Cambridge; New York: Cambridge University Press. p. 129. ISBN 0-521-28964-5.

Giaquinta, Mariano; Hildebrandt, Stefan (1996). Calculus of variations. Berlin; New York: Springer. p. 57. ISBN 3-540-50625-X.

Goh, C. J.; Yang, X.Q. (2002). Duality in optimization and variational inequalities. London; New York: Taylor & Francis. p. 13. ISBN 0-415-27479-6.

Soltan, V. (2021). Support and separation properties of convex sets in finite dimension. Extracta Math. Vol. 36, no. 2, 241-278.

[1] Luenberger, David G. (1969). Optimization by Vector Space Methods. New York: John Wiley & Sons. p. 133. ISBN 978-0-471-18117-0.

[Boyd-2] Boyd, Stephen P.; Vandenberghe, Lieven (2004). Convex Optimization (pdf). Cambridge University Press. pp. 50–51. ISBN 978-0-521-83378-3. Retrieved October 15, 2011.

[3] Cassels, John W. S. (1997), An Introduction to the Geometry of Numbers, Springer Classics in Mathematics (reprint of 1959[3] and 1971 Springer-Verlag ed.), Springer-Verlag.

[1]

[2]

[3]

Summary

Supporting hyperplane theorem edit

See also edit

Notes edit

References & further reading edit