
Summary
Thomae's function is a real-valued function of a real variable that can be defined as:[1]: 531
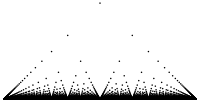
It is named after Carl Johannes Thomae, but has many other names: the popcorn function, the raindrop function, the countable cloud function, the modified Dirichlet function, the ruler function,[2] the Riemann function, or the Stars over Babylon (John Horton Conway's name).[3] Thomae mentioned it as an example for an integrable function with infinitely many discontinuities in an early textbook on Riemann's notion of integration.[4]
Since every rational number has a unique representation with coprime (also termed relatively prime) and , the function is well-defined. Note that is the only number in that is coprime to
It is a modification of the Dirichlet function, which is 1 at rational numbers and 0 elsewhere.
Properties edit
- Thomae's function is bounded and maps all real numbers to the unit interval:
- is periodic with period for all integers n and all real x.
Proof of periodicity
For all we also have and hence
For all there exist and such that and Consider . If divides and , it divides and . Conversely, if divides and , it divides and . So , and .
- is discontinuous at every rational number, so its points of discontinuity are dense within the real numbers.
Proof of discontinuity at rational numbers
Let be an arbitrary rational number, with and and coprime.
This establishes
Let be any irrational number and define for all
These are all irrational, and so for all
This implies and
Let , and given let For the corresponding we have
andwhich is exactly the definition of discontinuity of at .
- is continuous at every irrational number, so its points of continuity are dense within the real numbers.
Proof of continuity at irrational arguments
Since is periodic with period and it suffices to check all irrational points in Assume now and According to the Archimedean property of the reals, there exists with and there exist such that
for we have
The minimal distance of to its i-th lower and upper bounds equals
We define as the minimum of all the finitely many
so that for all andThis is to say, all these rational numbers are outside the -neighborhood of
Now let with the unique representation where are coprime. Then, necessarily, and therefore,
Likewise, for all irrational and thus, if then any choice of (sufficiently small) gives
Therefore, is continuous on
- is nowhere differentiable.
Proof of being nowhere differentiable
- For rational numbers, this follows from non-continuity.
- For irrational numbers:
- For any sequence of irrational numbers with for all that converges to the irrational point the sequence is identically and so
- According to Hurwitz's theorem, there also exists a sequence of rational numbers converging to with and coprime and
- Thus for all and so is not differentiable at all irrational
- has a strict local maximum at each rational number.[citation needed] See the proofs for continuity and discontinuity above for the construction of appropriate neighbourhoods, where has maxima.
- is Riemann integrable on any interval and the integral evaluates to over any set. The Lebesgue criterion for integrability states that a bounded function is Riemann integrable if and only if the set of all discontinuities has measure zero.[5] Every countable subset of the real numbers - such as the rational numbers - has measure zero, so the above discussion shows that Thomae's function is Riemann integrable on any interval. The function's integral is equal to over any set because the function is equal to zero almost everywhere.
- If is the graph of the restriction of to , then the box-counting dimension of is .[6]
Related probability distributions edit
Empirical probability distributions related to Thomae's function appear in DNA sequencing.[7] The human genome is diploid, having two strands per chromosome. When sequenced, small pieces ("reads") are generated: for each spot on the genome, an integer number of reads overlap with it. Their ratio is a rational number, and typically distributed similarly to Thomae's function.
If pairs of positive integers are sampled from a distribution and used to generate ratios , this gives rise to a distribution on the rational numbers. If the integers are independent the distribution can be viewed as a convolution over the rational numbers, . Closed form solutions exist for power-law distributions with a cut-off. If (where is the polylogarithm function) then . In the case of uniform distributions on the set , which is very similar to Thomae's function.[7]
Probability distributions related to Thomae's function can also be derived from recurrent processes generated by uniform discrete distributions. Such uniform discrete distributions can be pi digits, flips of a fair dice or live casino spins. In greater detail, the recurrent process is characterized as follows: A random variable Ci is repeatedly sampled N times from a discrete uniform distribution, where i ranges from 1 to N. For instance, consider integer values ranging from 1 to 10. Moments of occurrence, Tk, signify when events Ci repeat, defined as Ci = Ci-1 or Ci = Ci-2, where k ranges from 1 to M, with M being less than N. Subsequently, define Sj as the interval between successive Tk, representing the waiting time for an event to occur. Finally, introduce Zl as ln(Sj) – ln(Sj-1), where l ranges from 1 to U-1. The random variable Z displays fractal properties, resembling the shape distribution akin to Thomae's or Dirichlet function.[8]
The ruler function edit
For integers, the exponent of the highest power of 2 dividing gives 0, 1, 0, 2, 0, 1, 0, 3, 0, 1, 0, 2, 0, 1, 0, ... (sequence A007814 in the OEIS). If 1 is added, or if the 0s are removed, 1, 2, 1, 3, 1, 2, 1, 4, 1, 2, 1, 3, 1, 2, 1, ... (sequence A001511 in the OEIS). The values resemble tick-marks on a 1/16th graduated ruler, hence the name. These values correspond to the restriction of the Thomae function to the dyadic rationals: those rational numbers whose denominators are powers of 2.
Related functions edit
A natural follow-up question one might ask is if there is a function which is continuous on the rational numbers and discontinuous on the irrational numbers. This turns out to be impossible. The set of discontinuities of any function must be an Fσ set. If such a function existed, then the irrationals would be an Fσ set. The irrationals would then be the countable union of closed sets , but since the irrationals do not contain an interval, neither can any of the . Therefore, each of the would be nowhere dense, and the irrationals would be a meager set. It would follow that the real numbers, being the union of the irrationals and the rationals (which, as a countable set, is evidently meager), would also be a meager set. This would contradict the Baire category theorem: because the reals form a complete metric space, they form a Baire space, which cannot be meager in itself.
A variant of Thomae's function can be used to show that any Fσ subset of the real numbers can be the set of discontinuities of a function. If is a countable union of closed sets , define
Then a similar argument as for Thomae's function shows that has A as its set of discontinuities.
See also edit
- Blumberg theorem
- Cantor function
- Dirichlet function
- Euclid's orchard – Thomae's function can be interpreted as a perspective drawing of Euclid's orchard
- Volterra's function
References edit
- ^ Beanland, Kevin; Roberts, James W.; Stevenson, Craig (2009), "Modifications of Thomae's Function and Differentiability", The American Mathematical Monthly, 116 (6): 531–535, doi:10.4169/193009709x470425, JSTOR 40391145
- ^ Dunham, William (2008), The Calculus Gallery: Masterpieces from Newton to Lebesgue (Paperback ed.), Princeton: Princeton University Press, page 149, chapter 10, ISBN 978-0-691-13626-4,
...the so-called ruler function, a simple but provocative example that appeared in a work of Johannes Karl Thomae ... The graph suggests the vertical markings on a ruler—hence the name.
- ^ John Conway. "Topic: Provenance of a function". The Math Forum. Archived from the original on 13 June 2018.
- ^ Thomae, J. (1875), Einleitung in die Theorie der bestimmten Integrale (in German), Halle a/S: Verlag von Louis Nebert, p. 14, §20
- ^ Spivak, M. (1965), Calculus on manifolds, Perseus Books, page 53, Theorem 3-8, ISBN 978-0-8053-9021-6
- ^ Chen, Haipeng; Fraser, Jonathan M.; Yu, Han (2022). "Dimensions of the popcorn graph". Proceedings of the American Mathematical Society. 150 (11): 4729–4742. arXiv:2007.08407. doi:10.1090/proc/15729.
- ^ a b Trifonov, Vladimir; Pasqualucci, Laura; Dalla-Favera, Riccardo; Rabadan, Raul (2011). "Fractal-like Distributions over the Rational Numbers in High-throughput Biological and Clinical Data". Scientific Reports. 1 (191): 191. arXiv:1010.4328. Bibcode:2011NatSR...1E.191T. doi:10.1038/srep00191. PMC 3240948. PMID 22355706.
- ^ Endrit Dheskali. Generation of a recurrent fractal process using discrete uniform distributions, 26 February 2024, PREPRINT (Version 1) available at Research Square [1]
External links edit
- "Dirichlet-function", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Weisstein, Eric W. "Dirichlet Function". MathWorld.








