
Summary
The top quark, sometimes also referred to as the truth quark, (symbol: t) is the most massive of all observed elementary particles. It derives its mass from its coupling to the Higgs Boson. This coupling is very close to unity; in the Standard Model of particle physics, it is the largest (strongest) coupling at the scale of the weak interactions and above. The top quark was discovered in 1995 by the CDF[2] and DØ[3] experiments at Fermilab.
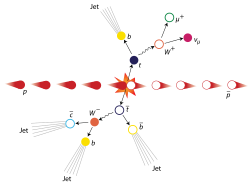 A collision event involving top quarks | |
| Composition | elementary particle |
|---|---|
| Statistics | fermionic |
| Family | quark |
| Generation | third |
| Interactions | strong, weak, electromagnetic, gravity |
| Symbol | t |
| Antiparticle | top antiquark ( t ) |
| Theorized | Makoto Kobayashi and Toshihide Maskawa (1973) |
| Discovered | CDF and DØ collaborations (1995) |
| Mass | 172.76±0.3 GeV/c2[1] |
| Decays into | bottom quark (99.8%) strange quark (0.17%) down quark (0.007%) |
| Electric charge | + 2 /3 e |
| Color charge | yes |
| Spin | 1 /2 ħ |
| Topness | 1 |
| Weak isospin | LH: + 1 /2, RH: 0 |
| Weak hypercharge | LH: +1 /3, RH: +4/3 |
Like all other quarks, the top quark is a fermion with spin 1 /2 and participates in all four fundamental interactions: gravitation, electromagnetism, weak interactions, and strong interactions. It has an electric charge of + 2 /3 e. It has a mass of 172.76±0.3 GeV/c2,[1] which is close to the rhenium atom mass.[4] The antiparticle of the top quark is the top antiquark (symbol: t, sometimes called antitop quark or simply antitop), which differs from it only in that some of its properties have equal magnitude but opposite sign.
The top quark interacts with gluons of the strong interaction and is typically produced in hadron colliders via this interaction. However, once produced, the top (or antitop) can decay only through the weak force. It decays to a W boson and either a bottom quark (most frequently), a strange quark, or, on the rarest of occasions, a down quark.[a]
The Standard Model determines the top quark's mean lifetime to be roughly 5×10−25 s.[5] This is about a twentieth of the timescale for strong interactions,[b] and therefore it does not form hadrons, giving physicists a unique opportunity to study a "bare" quark (all other quarks hadronize, meaning that they combine with other quarks to form hadrons and can only be observed as such).
Because the top quark is so massive, its properties allowed indirect determination of the mass of the Higgs boson (see § Mass and coupling to the Higgs boson below). As such, the top quark's properties are extensively studied as a means to discriminate between competing theories of new physics beyond the Standard Model. The top quark is the only quark that has been directly observed due to its decay time being shorter than the hadronization time.[b][6]
History edit
In 1973, Makoto Kobayashi and Toshihide Maskawa predicted the existence of a third generation of quarks to explain observed CP violations in kaon decay. The names top and bottom were introduced by Haim Harari in 1975,[7][8] to match the names of the first generation of quarks (up and down) reflecting the fact that the two were the "up" and "down" component of a weak isospin doublet.[9][10]
The proposal of Kobayashi and Maskawa heavily relied on the GIM mechanism put forward by Sheldon Glashow, John Iliopoulos and Luciano Maiani,[11] which predicted the existence of the then still unobserved charm quark. (The other second generation quark, the strange quark, was already detected in 1968.) When in November 1974 teams at Brookhaven National Laboratory (BNL) and the Stanford Linear Accelerator Center (SLAC) simultaneously announced the discovery of the J/ψ meson, it was soon after identified as a bound state of the missing charm quark with its antiquark. This discovery allowed the GIM mechanism to become part of the Standard Model.[12] With the acceptance of the GIM mechanism, Kobayashi and Maskawa's prediction also gained in credibility. Their case was further strengthened by the discovery of the tau by Martin Lewis Perl's team at SLAC between 1974 and 1978.[13] The tau announced a third generation of leptons, breaking the new symmetry between leptons and quarks introduced by the GIM mechanism. Restoration of the symmetry implied the existence of a fifth and sixth quark.
It was in fact not long until a fifth quark, the bottom, was discovered by the E288 experiment team, led by Leon Lederman at Fermilab in 1977.[14][15][16] This strongly suggested that there must also be a sixth quark, the top, to complete the pair. It was known that this quark would be heavier than the bottom, requiring more energy to create in particle collisions, but the general expectation was that the sixth quark would soon be found. However, it took another 18 years before the existence of the top was confirmed.[17]
Early searches for the top quark at SLAC and DESY (in Hamburg) came up empty-handed. When, in the early 1980s, the Super Proton Synchrotron (SPS) at CERN discovered the W boson and the Z boson, it was again felt that the discovery of the top was imminent. As the SPS gained competition from the Tevatron at Fermilab there was still no sign of the missing particle, and it was announced by the group at CERN that the top mass must be at least 41 GeV/c2. After a race between CERN and Fermilab to discover the top, the accelerator at CERN reached its limits without creating a single top, pushing the lower bound on its mass up to 77 GeV/c2.[17]
The Tevatron was (until the start of LHC operation at CERN in 2009) the only hadron collider powerful enough to produce top quarks. In order to be able to confirm a future discovery, a second detector, the DØ detector, was added to the complex (in addition to the Collider Detector at Fermilab (CDF) already present). In October 1992, the two groups found their first hint of the top, with a single creation event that appeared to contain the top. In the following years, more evidence was collected and on 22 April 1994, the CDF group submitted their article presenting tentative evidence for the existence of a top quark with a mass of about 175 GeV/c2. In the meantime, DØ had found no more evidence than the suggestive event in 1992. A year later, on 2 March 1995, after having gathered more evidence and reanalyzed the DØ data (which had been searched for a much lighter top), the two groups jointly reported the discovery of the top at a mass of 176±18 GeV/c2.[2][3][17]
In the years leading up to the top-quark discovery, it was realized that certain precision measurements of the electroweak vector boson masses and couplings are very sensitive to the value of the top-quark mass. These effects become much larger for higher values of the top mass and therefore could indirectly see the top quark even if it could not be directly detected in any experiment at the time. The largest effect from the top-quark mass was on the T parameter, and by 1994 the precision of these indirect measurements had led to a prediction of the top-quark mass to be between 145 GeV/c2 and 185 GeV/c2.[17] It is the development of techniques that ultimately allowed such precision calculations that led to Gerardus 't Hooft and Martinus Veltman winning the Nobel Prize in physics in 1999.[18][19]
Properties edit
- At the final Tevatron energy of 1.96 TeV, top–antitop pairs were produced with a cross section of about 7 picobarns (pb).[20] The Standard Model prediction (at next-to-leading order with mt = 175 GeV/c2) is 6.7~7.5 pb.
- The W bosons from top quark decays carry polarization from the parent particle, hence pose themselves as a unique probe to top polarization.
- In the Standard Model, the top quark is predicted to have a spin quantum number of 1 /2 and electric charge ++ 2 /3. A first measurement of the top quark charge has been published, resulting in some confidence that the top quark charge is indeed ++ 2 /3.[21]
Production edit
Because top quarks are very massive, large amounts of energy are needed to create one. The only way to achieve such high energies is through high-energy collisions. These occur naturally in the Earth's upper atmosphere as cosmic rays collide with particles in the air, or can be created in a particle accelerator. In 2011, after the Tevatron ceased operations, the Large Hadron Collider at CERN became the only accelerator that generates a beam of sufficient energy to produce top quarks, with a center-of-mass energy of 7 TeV. There are multiple processes that can lead to the production of top quarks, but they can be conceptually divided in two categories: top-pair production, and single-top production.
Top-quark pairs edit
The most common is production of a top–antitop pair via strong interactions. In a collision, a highly energetic gluon is created, which subsequently decays into a top and antitop. This process was responsible for the majority of the top events at Tevatron and was the process observed when the top was first discovered in 1995.[22] It is also possible to produce pairs of top–antitop through the decay of an intermediate photon or Z-boson. However, these processes are predicted to be much rarer and have a virtually identical experimental signature in a hadron collider like Tevatron.
Single top quarks edit
The production of single top quarks via weak interaction is a distinctly different process. This can happen in several ways (called channels): Either an intermediate W-boson decays into a top and antibottom quarks ("s-channel") or a bottom quark (probably created in a pair through the decay of a gluon) transforms to a top quark by exchanging a W boson with an up or down quark ("t-channel"). A single top quark can also be produced in association with a W boson, requiring an initial-state bottom quark ("tW-channel"). The first evidence for these processes was published by the DØ collaboration in December 2006,[23] and in March 2009 the CDF[24] and DØ[22] collaborations released twin articles with the definitive observation of these processes. The main significance of measuring these production processes is that their frequency is directly proportional to the |Vtb|2 component of the CKM matrix.
Decay edit
The only known way the top quark can decay is through the weak interaction, producing a W boson and a bottom quark.[a] Because of its enormous mass, the top quark is extremely short-lived, with a predicted lifetime of only 5×10−25 s.[5] As a result, top quarks do not have time before they decay to form hadrons as other quarks do.[b] The absence of a hadron surrounding the top quark provides physicists with the unique opportunity to study the behavior of a "bare" quark.
In particular, it is possible to directly determine the branching ratio:
The best current determination of this ratio is 0.957±0.034.[25] Since this ratio is equal to |Vtb|2 according to the Standard Model, this gives another way of determining the CKM element |Vtb|, or in combination with the determination of |Vtb| from single top production provides tests for the assumption that the CKM matrix is unitary.[26]
The Standard Model also allows more exotic decays, but only at one loop level, meaning that they are extremely rare. In particular, it is conceivable that a top quark might decay into another up-type quark (an up or a charm) by emitting a photon or a Z-boson.[27] However, searches for these exotic decay modes have produced no evidence that they occur, in accordance with expectations of the Standard Model. The branching ratios for these decays have been determined to be less than 1.8 in 10000 for photonic decay and less than 5 in 10000 for Z boson decay at 95% confidence.[25]
Mass and coupling to the Higgs boson edit
The Standard Model generates fermion masses through their couplings to the Higgs boson. This Higgs boson acts as a field filling space. Fermions interact with this field in proportion to their individual coupling constants which generates mass. A low-mass particle, such as the electron has a minuscule coupling while the top quark has the largest coupling to the Higgs,
In the Standard Model, all of the quark and lepton Higgs–Yukawa couplings are small compared to the top-quark Yukawa coupling. This hierarchy in the fermion masses remains a profound and open problem in theoretical physics. Higgs–Yukawa couplings are not fixed constants of nature, as their values vary slowly as the energy scale (distance scale) at which they are measured. These dynamics of Higgs–Yukawa couplings, called "running coupling constants", are due to a quantum effect called the renormalization group.
The Higgs–Yukawa couplings of the up, down, charm, strange and bottom quarks are hypothesized to have small values at the extremely high energy scale of grand unification, 1015 GeV. They increase in value at lower energy scales, at which the quark masses are generated by the Higgs. The slight growth is due to corrections from the QCD coupling. The corrections from the Yukawa couplings are negligible for the lower-mass quarks.
One of the prevailing views in particle physics is that the size of the top-quark Higgs–Yukawa coupling is determined by a unique nonlinear property of the renormalization group equation that describes the running of the large Higgs–Yukawa coupling of the top quark. If a quark Higgs–Yukawa coupling has a large value at very high energies, its Yukawa corrections will evolve downward in mass scale and cancel against the QCD corrections. This is known as a (quasi-) infrared fixed point, which was first predicted by B. Pendleton and G.G. Ross,[28] and by Christopher T. Hill,[29] No matter what the initial starting value of the coupling is, if sufficiently large, it will reach this fixed-point value. The corresponding quark mass is then predicted.
The top-quark Yukawa coupling lies very near the infrared fixed point of the Standard Model. The renormalization group equation is:
where g3 is the color gauge coupling, g2 is the weak isospin gauge coupling, and g1 is the weak hypercharge gauge coupling. This equation describes how the Yukawa coupling changes with energy scale μ. Solutions to this equation for large initial values yt cause the right-hand side of the equation to quickly approach zero, locking yt to the QCD coupling g3.
The value of the top quark fixed point is fairly precisely determined in the Standard Model, leading to a top-quark mass of 220 GeV. This is about 25% larger than the observed top mass and may be hinting at new physics at higher energy scales.
The quasi-infrared fixed point subsequently became the basis of top quark condensation and topcolor theories of electroweak symmetry breaking, in which the Higgs boson is composed of a pair of top and antitop quarks. The predicted top-quark mass comes into improved agreement with the fixed point if there are additional Higgs scalars beyond the standard model and therefore it may be hinting at a rich spectroscopy of new Higgs fields at energy scales that can be probed with the LHC and its upgrades.[30][31]
See also edit
Footnotes edit
- ^ a b The overwhelming majority of top quark decays produce a bottom quark, whose mass is closest to the top's. On very rare occasions it may decay into a strange quark; almost never a down quark.
- ^ a b c Top quark decay is an exceptional example of a weak process that is faster than a strong interaction.
References edit
- ^ a b Zyla, P.A.; et al. (Particle Data Group) (2020). "2020 Review of Particle Physics". Progress of Theoretical and Experimental Physics: 083C01.
- ^ a b
Abe, F.; et al. (CDF Collaboration) (1995). "Observation of top quark production in
p
p
collisions with the Collider-Detector at Fermilab". Physical Review Letters. 74 (14): 2626–2631. arXiv:hep-ex/9503002. Bibcode:1995PhRvL..74.2626A. doi:10.1103/PhysRevLett.74.2626. PMID 10057978. S2CID 119451328. - ^ a b Abachi, S.; et al. (DØ Collaboration) (1995). "Observation of the Top Quark". Physical Review Letters. 74 (14): 2632–2637. arXiv:hep-ex/9503003. Bibcode:1995PhRvL..74.2632A. doi:10.1103/PhysRevLett.74.2632. PMID 10057979. S2CID 42826202.
- ^ Elert, Glenn. "Quantum Chromodynamics". The Physics Hypertextbook. Retrieved 23 March 2019.
- ^ a b Quadt, A. (2006). "Top quark physics at hadron colliders". European Physical Journal C. 48 (3): 835–1000. Bibcode:2006EPJC...48..835Q. doi:10.1140/epjc/s2006-02631-6. S2CID 121887478.
- ^ Aubert, Jean-Jacques; Gastmans, Raymond; Gérard, Jean-Marc (6 December 2012). Particle Physics: Ideas and recent developments. Springer, Dordrecht. p. 69. ISBN 978-0-7923-6436-8. Retrieved 11 June 2020.
- ^ Harari, H. (1975). "A new quark model for hadrons". Physics Letters B. 57 (3): 265. Bibcode:1975PhLB...57..265H. doi:10.1016/0370-2693(75)90072-6.
- ^ Staley, K.W. (2004). The Evidence for the Top Quark. Cambridge University Press. pp. 31–33. ISBN 978-0-521-82710-2.
- ^ Perkins, D.H. (2000). Introduction to High Energy Physics. Cambridge University Press. p. 8. ISBN 978-0-521-62196-0.
- ^ Close, F. (2006). The New Cosmic Onion. CRC Press. p. 133. ISBN 978-1-58488-798-0.
- ^ Glashow, S.L.; Iliopoulous, J.; Maiani, L. (1970). "Weak interactions with lepton–hadron symmetry". Physical Review D. 2 (7): 1285–1292. Bibcode:1970PhRvD...2.1285G. doi:10.1103/PhysRevD.2.1285.
- ^ Pickering, A. (1999). Constructing Quarks: A sociological history of particle physics. University of Chicago Press. pp. 253–254. ISBN 978-0-226-66799-7.
- ^
Perl, M.L.; et al. (1975). "Evidence for anomalous lepton production in
e+
e−
annihilation". Physical Review Letters. 35 (22): 1489. Bibcode:1975PhRvL..35.1489P. doi:10.1103/PhysRevLett.35.1489. - ^ "Discovery of the bottom quark" (Press release). Discoveries at Fermilab. Fermilab. 7 August 1977. Retrieved 24 July 2009.
- ^ Lederman, L.M. (2005). "Logbook: Bottom quark". Symmetry Magazine. Vol. 2, no. 8. Archived from the original on 4 October 2006.
- ^ Herb, S.W.; et al. (1977). "Observation of a di‑muon resonance at 9.5 GeV in 400 GeV proton–nucleus collisions". Physical Review Letters. 39 (5): 252. Bibcode:1977PhRvL..39..252H. doi:10.1103/PhysRevLett.39.252. OSTI 1155396.
- ^ a b c d Liss, T.M.; Tipton, P.L. (1997). "The discovery of the top quark" (PDF). Scientific American. Vol. 277, no. 3. pp. 54–59. doi:10.1038/scientificamerican0997-54.
- ^ "The Nobel Prize in Physics 1999" (Press release). The Nobel Foundation. Retrieved 10 September 2009.
- ^ "The Nobel Prize in Physics 1999" (Press release). The Nobel Foundation. 12 October 1999. Retrieved 10 September 2009.
- ^ Chakraborty, D.; et al. (DØ collaboration & CDF collaboration) (2002). Top quark and W/Z results from the Tevatron (PDF). Rencontres de Moriond. p. 26. arXiv:hep-ex/0212027.
- ^ Abazov, V.M.; et al. (DØ Collaboration) (2007). "Experimental discrimination between charge 2e/3 top quark and charge 4e/3 exotic quark production scenarios". Physical Review Letters. 98 (4): 041801. arXiv:hep-ex/0608044. Bibcode:2007PhRvL..98d1801A. doi:10.1103/PhysRevLett.98.041801. hdl:10211.3/194390. PMID 17358756. S2CID 1147194.
- ^ a b Abazov, V.M.; et al. (DØ Collaboration) (2009). "Observation of Single Top Quark Production". Physical Review Letters. 103 (9): 092001. arXiv:0903.0850. Bibcode:2009PhRvL.103i2001A. doi:10.1103/PhysRevLett.103.092001. hdl:10211.3/194327. PMID 19792787. S2CID 14919683.
- ^ Abazov, V.M.; et al. (DØ Collaboration) (2007). "Evidence for production of single top quarks and first direct measurement of |Vtb|". Physical Review Letters. 98 (18): 181802. arXiv:hep-ex/0612052. Bibcode:2007PhRvL..98r1802A. doi:10.1103/PhysRevLett.98.181802. hdl:10211.3/194387. PMID 17501561. S2CID 14937909.
- ^ Aaltonen, T.; et al. (CDF Collaboration) (2009). "First observation of electroweak single top quark production". Physical Review Letters. 103 (9): 092002. arXiv:0903.0885. Bibcode:2009PhRvL.103i2002A. doi:10.1103/PhysRevLett.103.092002. hdl:1721.1/52314. PMID 19792788. S2CID 8029289.
- ^ a b Zyla, P.A.; et al. (Particle Data Group) (2020). "QUARKS" (PDF). Progress of Theoretical and Experimental Physics: 083C01. Retrieved 22 May 2022.
- ^ Abazov, V.M.; et al. (DØ Collaboration) (2008). "Simultaneous measurement of the ratio B(t → Wb)/B(t → Wq) and the top-quark pair production cross section with the DØ detector at √s = 1.96 TeV". Physical Review Letters. 100 (19): 192003. arXiv:0801.1326. Bibcode:2008PhRvL.100s2003A. doi:10.1103/PhysRevLett.100.192003. hdl:10211.3/194369. PMID 18518440. S2CID 2638258.
- ^ Chekanov, S.; et al. (ZEUS Collaboration) (2003). "Search for single-top production in e-p collisions at HERA". Physics Letters B. 559 (3–4): 153–170. arXiv:hep-ex/0302010. Bibcode:2003PhLB..559..153Z. doi:10.1016/S0370-2693(03)00333-2. S2CID 119494760.
- ^ Pendleton, Brian; Ross, Graham (1981). "Mass and mixing angle predictions from infrared fixed points". Physics Letters. 98B (4): 291–294. Bibcode:1981PhLB...98..291P. doi:10.1016/0370-2693(81)90017-4.
- ^ Hill, Christopher T. (1981). "Quark and lepton masses from renormalization group fixed points". Physical Review D. 24 (3): 691–703. Bibcode:1981PhRvD..24..691H. doi:10.1103/PhysRevD.24.691.
- ^ Hill, Christopher T.; Machado, Pedro; Thomsen, Anders; Turner, Jessica (2019). "Where are the next Higgs bosons?". Physical Review D. 100 (1): 015051. arXiv:1904.04257. Bibcode:2019PhRvD.100a5051H. doi:10.1103/PhysRevD.100.015051. S2CID 104291827.
- ^ Hill, Christopher T.; Machado, Pedro; Thomsen, Anders; Turner, Jessica (2019). "Scalar democracy". Physical Review D. 100 (1): 015015. arXiv:1902.07214. Bibcode:2019PhRvD.100a5015H. doi:10.1103/PhysRevD.100.015015. S2CID 119193325.
Further reading edit
- Frank Fiedler; for the D0; CDF Collaborations (June 2005). "Top Quark Production and Properties at the Tevatron". arXiv:hep-ex/0506005.
{{cite arXiv}}: CS1 maint: numeric names: authors list (link)
- R. Nave. "Quarks". HyperPhysics. Georgia State University, Department of Physics and Astronomy. Retrieved 29 June 2008.
- A. Pickering (1984). Constructing Quarks. University of Chicago Press. pp. 114–125. ISBN 978-0-226-66799-7.
External links edit
- "Script to retrieve "top quark" on arxiv.org". Archived from the original on 16 January 2022. Retrieved 19 February 2023.
- "Tevatron Electroweak Working Group". Fermilab.
- "Top quark information". Fermilab.
- "CDF and DZero collaborations' top quark discovery". Symmetry Magazine (discovery logbook pages). Archived from the original on 2 October 2006.
- "article on the discovery of the top quark" (PDF). Scientific American.
- "Top quark analysis results from DØ Collaboration". Fermilab (public homepage).
- "Top quark analysis results from CDF Collaboration". Fermilab.
- "article about the 1994 top quark discovery". Harvard Magazine. Archived from the original on 8 May 2006.
- "Nobel Prize in Physics". 1999.



