
Summary
In physics and mathematics, continuous translational symmetry is the invariance of a system of equations under any translation (without rotation). Discrete translational symmetry is invariant under discrete translation.
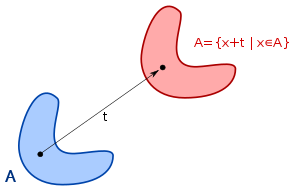
Analogously, an operator A on functions is said to be translationally invariant with respect to a translation operator if the result after applying A doesn't change if the argument function is translated. More precisely it must hold that
Laws of physics are translationally invariant under a spatial translation if they do not distinguish different points in space. According to Noether's theorem, space translational symmetry of a physical system is equivalent to the momentum conservation law.
Translational symmetry of an object means that a particular translation does not change the object. For a given object, the translations for which this applies form a group, the symmetry group of the object, or, if the object has more kinds of symmetry, a subgroup of the symmetry group.
Geometry edit
Translational invariance implies that, at least in one direction, the object is infinite: for any given point p, the set of points with the same properties due to the translational symmetry form the infinite discrete set {p + na | n ∈ Z} = p + Z a. Fundamental domains are e.g. H + [0, 1] a for any hyperplane H for which a has an independent direction. This is in 1D a line segment, in 2D an infinite strip, and in 3D a slab, such that the vector starting at one side ends at the other side. Note that the strip and slab need not be perpendicular to the vector, hence can be narrower or thinner than the length of the vector.
In spaces with dimension higher than 1, there may be multiple translational symmetry. For each set of k independent translation vectors, the symmetry group is isomorphic with Zk. In particular, the multiplicity may be equal to the dimension. This implies that the object is infinite in all directions. In this case, the set of all translations forms a lattice. Different bases of translation vectors generate the same lattice if and only if one is transformed into the other by a matrix of integer coefficients of which the absolute value of the determinant is 1. The absolute value of the determinant of the matrix formed by a set of translation vectors is the hypervolume of the n-dimensional parallelepiped the set subtends (also called the covolume of the lattice). This parallelepiped is a fundamental region of the symmetry: any pattern on or in it is possible, and this defines the whole object. See also lattice (group).
E.g. in 2D, instead of a and b we can also take a and a − b, etc. In general in 2D, we can take pa + qb and ra + sb for integers p, q, r, and s such that ps − qr is 1 or −1. This ensures that a and b themselves are integer linear combinations of the other two vectors. If not, not all translations are possible with the other pair. Each pair a, b defines a parallelogram, all with the same area, the magnitude of the cross product. One parallelogram fully defines the whole object. Without further symmetry, this parallelogram is a fundamental domain. The vectors a and b can be represented by complex numbers. For two given lattice points, equivalence of choices of a third point to generate a lattice shape is represented by the modular group, see lattice (group).
Alternatively, e.g. a rectangle may define the whole object, even if the translation vectors are not perpendicular, if it has two sides parallel to one translation vector, while the other translation vector starting at one side of the rectangle ends at the opposite side.
For example, consider a tiling with equal rectangular tiles with an asymmetric pattern on them, all oriented the same, in rows, with for each row a shift of a fraction, not one half, of a tile, always the same, then we have only translational symmetry, wallpaper group p1 (the same applies without shift). With rotational symmetry of order two of the pattern on the tile we have p2 (more symmetry of the pattern on the tile does not change that, because of the arrangement of the tiles). The rectangle is a more convenient unit to consider as fundamental domain (or set of two of them) than a parallelogram consisting of part of a tile and part of another one.
In 2D there may be translational symmetry in one direction for vectors of any length. One line, not in the same direction, fully defines the whole object. Similarly, in 3D there may be translational symmetry in one or two directions for vectors of any length. One plane (cross-section) or line, respectively, fully defines the whole object.
Examples edit
- Frieze patterns all have translational symmetries, and sometimes other kinds.
- The Fourier transform with subsequent computation of absolute values is a translation-invariant operator.
- The mapping from a polynomial function to the polynomial degree is a translation-invariant functional.
- The Lebesgue measure is a complete translation-invariant measure.
See also edit
References edit
- Stenger, Victor J. (2000) and MahouShiroUSA (2007). Timeless Reality. Prometheus Books. Especially chpt. 12. Nontechnical.






