
Summary
 Icosidodecahedron |
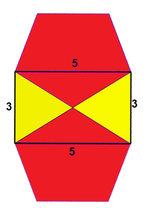 Vertex figure represented as 3.5.3.5 or (3.5)2 |
In geometry, a vertex configuration[1][2][3][4] is a shorthand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron. (Chiral polyhedra exist in mirror-image pairs with the same vertex configuration.)
A vertex configuration is given as a sequence of numbers representing the number of sides of the faces going around the vertex. The notation "a.b.c" describes a vertex that has 3 faces around it, faces with a, b, and c sides.
For example, "3.5.3.5" indicates a vertex belonging to 4 faces, alternating triangles and pentagons. This vertex configuration defines the vertex-transitive icosidodecahedron. The notation is cyclic and therefore is equivalent with different starting points, so 3.5.3.5 is the same as 5.3.5.3. The order is important, so 3.3.5.5 is different from 3.5.3.5 (the first has two triangles followed by two pentagons). Repeated elements can be collected as exponents so this example is also represented as (3.5)2.
It has variously been called a vertex description,[5][6][7] vertex type,[8][9] vertex symbol,[10][11] vertex arrangement,[12] vertex pattern,[13] face-vector.[14] It is also called a Cundy and Rollett symbol for its usage for the Archimedean solids in their 1952 book Mathematical Models.[15][16][17]
Vertex figures edit
A vertex configuration can also be represented as a polygonal vertex figure showing the faces around the vertex. This vertex figure has a 3-dimensional structure since the faces are not in the same plane for polyhedra, but for vertex-uniform polyhedra all the neighboring vertices are in the same plane and so this plane projection can be used to visually represent the vertex configuration.
Variations and uses edit
| {3,3} = 33 Defect 180° |
{3,4} = 34 Defect 120° |
{3,5} = 35 Defect 60° |
{3,6} = 36 |
| {4,3} Defect 90° |
{4,4} = 44 |
{5,3} = 53 Defect 36° |
{6,3} = 63 |
| A vertex needs at least 3 faces, and an angle defect. A 0° angle defect will fill the Euclidean plane with a regular tiling. By Descartes' theorem, the number of vertices is 720°/defect (4π radians/defect). | |||
Different notations are used, sometimes with a comma (,) and sometimes a period (.) separator. The period operator is useful because it looks like a product and an exponent notation can be used. For example, 3.5.3.5 is sometimes written as (3.5)2.
The notation can also be considered an expansive form of the simple Schläfli symbol for regular polyhedra. The Schläfli notation {p,q} means q p-gons around each vertex. So {p,q} can be written as p.p.p... (q times) or pq. For example, an icosahedron is {3,5} = 3.3.3.3.3 or 35.
This notation applies to polygonal tilings as well as polyhedra. A planar vertex configuration denotes a uniform tiling just like a nonplanar vertex configuration denotes a uniform polyhedron.
The notation is ambiguous for chiral forms. For example, the snub cube has clockwise and counterclockwise forms which are identical across mirror images. Both have a 3.3.3.3.4 vertex configuration.
Star polygons edit
The notation also applies for nonconvex regular faces, the star polygons. For example, a pentagram has the symbol {5/2}, meaning it has 5 sides going around the centre twice.
For example, there are 4 regular star polyhedra with regular polygon or star polygon vertex figures. The small stellated dodecahedron has the Schläfli symbol of {5/2,5} which expands to an explicit vertex configuration 5/2.5/2.5/2.5/2.5/2 or combined as (5/2)5. The great stellated dodecahedron, {5/2,3} has a triangular vertex figure and configuration (5/2.5/2.5/2) or (5/2)3. The great dodecahedron, {5,5/2} has a pentagrammic vertex figure, with vertex configuration is (5.5.5.5.5)/2 or (55)/2. A great icosahedron, {3,5/2} also has a pentagrammic vertex figure, with vertex configuration (3.3.3.3.3)/2 or (35)/2.
| {5/2,5} = (5/2)5 | {5/2,3} = (5/2)3 | 34.5/2 | 34.5/3 | (34.5/2)/2 |
|---|---|---|---|---|
| {5,5/2} = (55)/2 | {3,5/2} = (35)/2 | V.34.5/2 | V34.5/3 | V(34.5/2)/2 |
Inverted polygons edit
Faces on a vertex figure are considered to progress in one direction. Some uniform polyhedra have vertex figures with inversions where the faces progress retrograde. A vertex figure represents this in the star polygon notation of sides p/q such that p<2q, where p is the number of sides and q the number of turns around a circle. For example, "3/2" means a triangle that has vertices that go around twice, which is the same as backwards once. Similarly "5/3" is a backwards pentagram 5/2.
All uniform vertex configurations of regular convex polygons edit
Semiregular polyhedra have vertex configurations with positive angle defect.
NOTE: The vertex figure can represent a regular or semiregular tiling on the plane if its defect is zero. It can represent a tiling of the hyperbolic plane if its defect is negative.
For uniform polyhedra, the angle defect can be used to compute the number of vertices. Descartes' theorem states that all the angle defects in a topological sphere must sum to 4π radians or 720 degrees.
Since uniform polyhedra have all identical vertices, this relation allows us to compute the number of vertices, which is 4π/defect or 720/defect.
Example: A truncated cube 3.8.8 has an angle defect of 30 degrees. Therefore, it has 720/30 = 24 vertices.
In particular it follows that {a,b} has 4 / (2 - b(1 - 2/a)) vertices.
Every enumerated vertex configuration potentially uniquely defines a semiregular polyhedron. However, not all configurations are possible.
Topological requirements limit existence. Specifically p.q.r implies that a p-gon is surrounded by alternating q-gons and r-gons, so either p is even or q equals r. Similarly q is even or p equals r, and r is even or p equals q. Therefore, potentially possible triples are 3.3.3, 3.4.4, 3.6.6, 3.8.8, 3.10.10, 3.12.12, 4.4.n (for any n>2), 4.6.6, 4.6.8, 4.6.10, 4.6.12, 4.8.8, 5.5.5, 5.6.6, 6.6.6. In fact, all these configurations with three faces meeting at each vertex turn out to exist.
The number in parentheses is the number of vertices, determined by the angle defect.
- Triples
- Platonic solids 3.3.3 (4), 4.4.4 (8), 5.5.5 (20)
- prisms 3.4.4 (6), 4.4.4 (8; also listed above), 4.4.n (2n)
- Archimedean solids 3.6.6 (12), 3.8.8 (24), 3.10.10 (60), 4.6.6 (24), 4.6.8 (48), 4.6.10 (120), 5.6.6 (60).
- regular tiling 6.6.6
- semiregular tilings 3.12.12, 4.6.12, 4.8.8
- Quadruples
- Platonic solid 3.3.3.3 (6)
- antiprisms 3.3.3.3 (6; also listed above), 3.3.3.n (2n)
- Archimedean solids 3.4.3.4 (12), 3.5.3.5 (30), 3.4.4.4 (24), 3.4.5.4 (60)
- regular tiling 4.4.4.4
- semiregular tilings 3.6.3.6, 3.4.6.4
- Quintuples
- Platonic solid 3.3.3.3.3 (12)
- Archimedean solids 3.3.3.3.4 (24), 3.3.3.3.5 (60) (both chiral)
- semiregular tilings 3.3.3.3.6 (chiral), 3.3.3.4.4, 3.3.4.3.4 (note that the two different orders of the same numbers give two different patterns)
- Sextuples
- regular tiling 3.3.3.3.3.3
Face configuration edit
The uniform dual or Catalan solids, including the bipyramids and trapezohedra, are vertically-regular (face-transitive) and so they can be identified by a similar notation which is sometimes called face configuration.[3] Cundy and Rollett prefixed these dual symbols by a V. In contrast, Tilings and patterns uses square brackets around the symbol for isohedral tilings.
This notation represents a sequential count of the number of faces that exist at each vertex around a face.[18] For example, V3.4.3.4 or V(3.4)2 represents the rhombic dodecahedron which is face-transitive: every face is a rhombus, and alternating vertices of the rhombus contain 3 or 4 faces each.
Notes edit
- ^ Uniform Solution for Uniform Polyhedra Archived 2015-11-27 at the Wayback Machine (1993)
- ^ The Uniform Polyhedra Roman E. Maeder (1995)
- ^ a b Crystallography of Quasicrystals: Concepts, Methods and Structures by Walter Steurer, Sofia Deloudi, (2009) pp. 18–20 and 51–53
- ^ Physical Metallurgy: 3-Volume Set, Volume 1 edited by David E. Laughlin, (2014) pp. 16–20
- ^ Archimedean Polyhedra Archived 2017-07-05 at the Wayback Machine Steven Dutch
- ^ Uniform Polyhedra Jim McNeill
- ^ Uniform Polyhedra and their Duals Robert Webb
- ^ Symmetry-type graphs of Platonic and Archimedean solids, Jurij Kovič, (2011)
- ^ 3. General Theorems: Regular and Semi-Regular Tilings Kevin Mitchell, 1995
- ^ Resources for Teaching Discrete Mathematics: Classroom Projects, History, modules, and articles, edited by Brian Hopkins
- ^ Vertex Symbol Robert Whittaker
- ^ Structure and Form in Design: Critical Ideas for Creative Practice By Michael Hann
- ^ Symmetry-type graphs of Platonic and Archimedean solids Jurij Kovič
- ^ Deza, Michel; Shtogrin, Mikhail (2000), "Uniform partitions of 3-space, their relatives and embedding", European Journal of Combinatorics, 21 (6): 807–814, arXiv:math/9906034, doi:10.1006/eujc.1999.0385, MR 1791208
- ^ Weisstein, Eric W., "Archimedean solid", MathWorld
- ^ Divided Spheres: Geodesics and the Orderly Subdivision of the Sphere 6.4.1 Cundy-Rollett symbol, p. 164
- ^ Laughlin (2014), p. 16
- ^ Cundy and Rollett (1952)
References edit
- Cundy, H. and Rollett, A., Mathematical Models (1952), (3rd edition, 1989, Stradbroke, England: Tarquin Pub.), 3.7 The Archimedean Polyhedra. Pp. 101–115, pp. 118–119 Table I, Nets of Archimedean Duals, V.a.b.c... as vertically-regular symbols.
- Peter Cromwell, Polyhedra, Cambridge University Press (1977) The Archimedean solids. Pp. 156–167.
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. Uses Cundy-Rollett symbol.
- Grünbaum, Branko; Shephard, G. C. (1987). Tilings and Patterns. W. H. Freeman and Company. ISBN 0-7167-1193-1. Pp. 58–64, Tilings of regular polygons a.b.c.... (Tilings by regular polygons and star polygons) pp. 95–97, 176, 283, 614–620, Monohedral tiling symbol [v1.v2. ... .vr]. pp. 632–642 hollow tilings.
- The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, ISBN 978-1-56881-220-5 (p. 289 Vertex figures, uses comma separator, for Archimedean solids and tilings).
External links edit
- Consistent Vertex Descriptions Stella (software), Robert Webb


