
Summary
In topology, the wedge sum is a "one-point union" of a family of topological spaces. Specifically, if X and Y are pointed spaces (i.e. topological spaces with distinguished basepoints and ) the wedge sum of X and Y is the quotient space of the disjoint union of X and Y by the identification
where is the equivalence closure of the relation More generally, suppose is a indexed family of pointed spaces with basepoints The wedge sum of the family is given by:
The wedge sum is again a pointed space, and the binary operation is associative and commutative (up to homeomorphism).
Sometimes the wedge sum is called the wedge product, but this is not the same concept as the exterior product, which is also often called the wedge product.
Examples edit
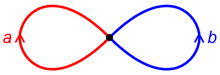
The wedge sum of two circles is homeomorphic to a figure-eight space. The wedge sum of circles is often called a bouquet of circles, while a wedge product of arbitrary spheres is often called a bouquet of spheres.
A common construction in homotopy is to identify all of the points along the equator of an -sphere . Doing so results in two copies of the sphere, joined at the point that was the equator:
Let be the map that is, of identifying the equator down to a single point. Then addition of two elements of the -dimensional homotopy group of a space at the distinguished point can be understood as the composition of and with :
Here, are maps which take a distinguished point to the point Note that the above uses the wedge sum of two functions, which is possible precisely because they agree at the point common to the wedge sum of the underlying spaces.
Categorical description edit
The wedge sum can be understood as the coproduct in the category of pointed spaces. Alternatively, the wedge sum can be seen as the pushout of the diagram in the category of topological spaces (where is any one-point space).
Properties edit
Van Kampen's theorem gives certain conditions (which are usually fulfilled for well-behaved spaces, such as CW complexes) under which the fundamental group of the wedge sum of two spaces and is the free product of the fundamental groups of and
See also edit
- Smash product
- Hawaiian earring, a topological space resembling, but not the same as, a wedge sum of countably many circles
References edit
- Rotman, Joseph. An Introduction to Algebraic Topology, Springer, 2004, p. 153. ISBN 0-387-96678-1













