
Summary
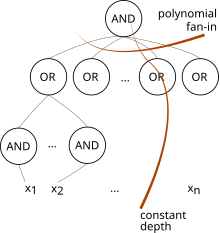
AC0 is a complexity class used in circuit complexity. It is the smallest class in the AC hierarchy, and consists of all families of circuits of depth O(1) and polynomial size, with unlimited-fanin AND gates and OR gates (we allow NOT gates only at the inputs).[1] It thus contains NC0, which has only bounded-fanin AND and OR gates.[1]
Example problems edit
Integer addition and subtraction are computable in AC0,[2] but multiplication is not (specifically, when the inputs are two integers under the usual binary[3] or base-10 representations of integers).
Since it is a circuit class, like P/poly, AC0 also contains every unary language.
Descriptive complexity edit
From a descriptive complexity viewpoint, DLOGTIME-uniform AC0 is equal to the descriptive class FO+BIT of all languages describable in first-order logic with the addition of the BIT predicate, or alternatively by FO(+, ×), or by Turing machine in the logarithmic hierarchy.[4]
Separations edit
In 1984 Furst, Saxe, and Sipser showed that calculating the parity of the input bits (unlike the aforementioned addition/subtraction problems above which had two inputs) cannot be decided by any AC0 circuits, even with non-uniformity.[5][1] It follows that AC0 is not equal to NC1, because a family of circuits in the latter class can compute parity.[1] More precise bounds follow from switching lemma. Using them, it has been shown that there is an oracle separation between the polynomial hierarchy and PSPACE.
References edit
- ^ a b c d Arora, Sanjeev; Barak, Boaz (2009). Computational complexity. A modern approach. Cambridge University Press. pp. 117–118, 287. ISBN 978-0-521-42426-4. Zbl 1193.68112.
- ^ Barrington, David Mix; Maciel, Alexis (July 18, 2000). "Lecture 2: The Complexity of Some Problems" (PDF). IAS/PCMI Summer Session 2000, Clay Mathematics Undergraduate Program: Basic Course on Computational Complexity.
- ^ Kayal, Neeraj; Hegde, Sumant (2015). "Lecture 5: Feb 4, 2015" (PDF). E0 309: Topics in Complexity Theory. Archived (PDF) from the original on 2021-10-16. Retrieved 2021-10-16.
- ^ Immerman, N. (1999). Descriptive Complexity. Springer. p. 85.
- ^ Furst, Merrick; Saxe, James B.; Sipser, Michael (1984). "Parity, circuits, and the polynomial-time hierarchy". Mathematical Systems Theory. 17 (1): 13–27. doi:10.1007/BF01744431. MR 0738749. Zbl 0534.94008.


