
Summary
In mathematics, an antimatroid is a formal system that describes processes in which a set is built up by including elements one at a time, and in which an element, once available for inclusion, remains available until it is included.[1] Antimatroids are commonly axiomatized in two equivalent ways, either as a set system modeling the possible states of such a process, or as a formal language modeling the different sequences in which elements may be included. Dilworth (1940) was the first to study antimatroids, using yet another axiomatization based on lattice theory, and they have been frequently rediscovered in other contexts.[2]
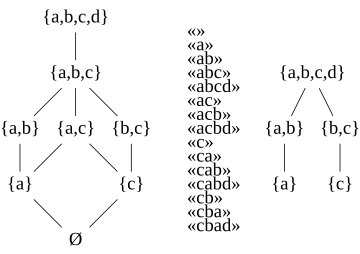
The axioms defining antimatroids as set systems are very similar to those of matroids, but whereas matroids are defined by an exchange axiom, antimatroids are defined instead by an anti-exchange axiom, from which their name derives. Antimatroids can be viewed as a special case of greedoids and of semimodular lattices, and as a generalization of partial orders and of distributive lattices. Antimatroids are equivalent, by complementation, to convex geometries, a combinatorial abstraction of convex sets in geometry.
Antimatroids have been applied to model precedence constraints in scheduling problems, potential event sequences in simulations, task planning in artificial intelligence, and the states of knowledge of human learners.
Definitions edit
An antimatroid can be defined as a finite family of finite sets, called feasible sets, with the following two properties:[3]
- The union of any two feasible sets is also feasible. That is, is closed under unions.
- If is a nonempty feasible set, then contains an element for which (the set formed by removing from ) is also feasible. That is, is an accessible set system.
Antimatroids also have an equivalent definition as a formal language, that is, as a set of strings defined from a finite alphabet of symbols. A string that belongs to this set is called a word of the language. A language defining an antimatroid must satisfy the following properties:[4]
- Every symbol of the alphabet occurs in at least one word of .
- Each word of contains at most one copy of each symbol. A language with this property is called normal.[5]
- Every prefix of a word in is also in . A language with this property is called hereditary.[5]
- If and are words in , and contains at least one symbol that is not in , then there is a symbol in such that the concatenation is another word in .
The equivalence of these two forms of definition can be seen as follows. If is an antimatroid defined as a formal language, then the sets of symbols in words of form an accessible union-closed set system. It is accessible by the hereditary property of strings, and it can be shown to be union-closed by repeated application of the concatenation property of strings. In the other direction, from an accessible union-closed set system , the language of normal strings whose prefixes all have sets of symbols belonging to meets the requirements for a formal language to be an antimatroid. These two transformations are the inverses of each other: transforming a formal language into a set family and back, or vice versa, produces the same system. Thus, these two definitions lead to mathematically equivalent classes of objects.[6]
Examples edit
The following systems provide examples of antimatroids:
- Chain antimatroids
- The prefixes of a single string, and the sets of symbols in these prefixes, form an antimatroid. For instance the chain antimatroid defined by the string has as its formal language the set of strings (where denotes the empty string) and as its family of feasible sets the family[7]
- Poset antimatroids
- The lower sets of a finite partially ordered set form an antimatroid, with the full-length words of the antimatroid forming the linear extensions of the partial order.[8] By Birkhoff's representation theorem for distributive lattices, the feasible sets in a poset antimatroid (ordered by set inclusion) form a distributive lattice, and all distributive lattices can be formed in this way. Thus, antimatroids can be seen as generalizations of distributive lattices. A chain antimatroid is the special case of a poset antimatroid for a total order.[7]
- Shelling antimatroids
- A shelling sequence of a finite set of points in the Euclidean plane or a higher-dimensional Euclidean space is formed by repeatedly removing vertices of the convex hull. The feasible sets of the antimatroid formed by these sequences are the intersections of with the complement of a convex set.[7]
- Perfect elimination
- A perfect elimination ordering of a chordal graph is an ordering of its vertices such that, for each vertex , the neighbors of that occur later than in the ordering form a clique. The prefixes of perfect elimination orderings of a chordal graph form an antimatroid.[9]
- Chip-firing games
- Chip-firing games such as the abelian sandpile model are defined by a directed graph together with a system of "chips" placed on its vertices. Whenever the number of chips on a vertex is at least as large as the number of edges out of , it is possible to fire , moving one chip to each neighboring vertex. The event that fires for the th time can only happen if it has already fired times and accumulated total chips. These conditions do not depend on the ordering of previous firings, and remain true until fires, so any given graph and initial placement of chips for which the system terminates defines an antimatroid on the pairs . A consequence of the antimatroid property of these systems is that, for a given initial state, the number of times each vertex fires and the eventual stable state of the system do not depend on the firing order.[10]
Paths and basic words edit
In the set theoretic axiomatization of an antimatroid there are certain special sets called paths that determine the whole antimatroid, in the sense that the sets of the antimatroid are exactly the unions of paths.[11] If is any feasible set of the antimatroid, an element that can be removed from to form another feasible set is called an endpoint of , and a feasible set that has only one endpoint is called a path of the antimatroid.[12] The family of paths can be partially ordered by set inclusion, forming the path poset of the antimatroid.[13]
For every feasible set in the antimatroid, and every element of , one may find a path subset of for which is an endpoint: to do so, remove one at a time elements other than until no such removal leaves a feasible subset. Therefore, each feasible set in an antimatroid is the union of its path subsets.[11] If is not a path, each subset in this union is a proper subset of . But, if is itself a path with endpoint , each proper subset of that belongs to the antimatroid excludes . Therefore, the paths of an antimatroid are exactly the feasible sets that do not equal the unions of their proper feasible subsets. Equivalently, a given family of sets forms the family of paths of an antimatroid if and only if, for each in , the union of subsets of in has one fewer element than itself.[14] If so, itself is the family of unions of subsets of .[11]
In the formal language formalization of an antimatroid, the longest strings are called basic words. Each basic word forms a permutation of the whole alphabet.[15] If is the set of basic words, can be defined from as the set of prefixes of words in .[16]
Convex geometries edit
If is the set system defining an antimatroid, with equal to the union of the sets in , then the family of sets
A convex geometry can also be defined in terms of a closure operator that maps any subset of to its minimal closed superset. To be a closure operator, should have the following properties:[18]
- : the closure of the empty set is empty.
- For every subset of , is a subset of and .
- Whenever , is a subset of .
The family of closed sets resulting from a closure operation of this type is necessarily closed under intersections, but might not be a convex geometry. The closure operators that define convex geometries also satisfy an additional anti-exchange axiom:
- If is a subset of , and and are distinct elements of that do not belong to , but does belong to , then does not belong to .[18]
A closure operation satisfying this axiom is called an anti-exchange closure. If is a closed set in an anti-exchange closure, then the anti-exchange axiom determines a partial order on the elements not belonging to , where in the partial order when belongs to . If is a minimal element of this partial order, then is closed. That is, the family of closed sets of an anti-exchange closure has the property that for any set other than the universal set there is an element that can be added to it to produce another closed set. This property is complementary to the accessibility property of antimatroids, and the fact that intersections of closed sets are closed is complementary to the property that unions of feasible sets in an antimatroid are feasible. Therefore, the complements of the closed sets of any anti-exchange closure form an antimatroid.[17]
The undirected graphs in which the convex sets (subsets of vertices that contain all shortest paths between vertices in the subset) form a convex geometry are exactly the Ptolemaic graphs.[19]
Join-distributive lattices edit
Every two feasible sets of an antimatroid have a unique least upper bound (their union) and a unique greatest lower bound (the union of the sets in the antimatroid that are contained in both of them). Therefore, the feasible sets of an antimatroid, partially ordered by set inclusion, form a lattice. Various important features of an antimatroid can be interpreted in lattice-theoretic terms; for instance the paths of an antimatroid are the join-irreducible elements of the corresponding lattice, and the basic words of the antimatroid correspond to maximal chains in the lattice. The lattices that arise from antimatroids in this way generalize the finite distributive lattices, and can be characterized in several different ways.
- The description originally considered by Dilworth (1940) concerns meet-irreducible elements of the lattice. For each element of an antimatroid, there exists a unique maximal feasible set that does not contain : can be constructed as the union of all feasible sets not containing . This set is automatically meet-irreducible, meaning that it is not the meet of any two larger lattice elements. This is true because every feasible superset of contains , and the same is therefore also true of every intersection of feasible supersets. Every element of an arbitrary lattice can be decomposed as a meet of meet-irreducible sets, often in multiple ways, but in the lattice corresponding to an antimatroid each element has a unique minimal family of meet-irreducible sets whose meet is ; this family consists of the sets for the elements such that is feasible. That is, the lattice has unique meet-irreducible decompositions.
- A second characterization concerns the intervals in the lattice, the sublattices defined by a pair of lattice elements consisting of all lattice elements with . An interval is atomistic if every element in it is the join of atoms (the minimal elements above the bottom element ), and it is Boolean if it is isomorphic to the lattice of all subsets of a finite set. For an antimatroid, every interval that is atomistic is also boolean.
- Thirdly, the lattices arising from antimatroids are semimodular lattices, lattices that satisfy the upper semimodular law that for every two elements and , if covers then covers . Translating this condition into the feasible sets of an antimatroid, if a feasible set has only one element not belonging to another feasible set then that one element may be added to to form another set in the antimatroid. Additionally, the lattice of an antimatroid has the meet-semidistributive property: for all lattice elements , , and , if and equal each other then they also both equal . A semimodular and meet-semidistributive lattice is called a join-distributive lattice.
These three characterizations are equivalent: any lattice with unique meet-irreducible decompositions has boolean atomistic intervals and is join-distributive, any lattice with boolean atomistic intervals has unique meet-irreducible decompositions and is join-distributive, and any join-distributive lattice has unique meet-irreducible decompositions and boolean atomistic intervals.[20] Thus, we may refer to a lattice with any of these three properties as join-distributive. Any antimatroid gives rise to a finite join-distributive lattice, and any finite join-distributive lattice comes from an antimatroid in this way.[21] Another equivalent characterization of finite join-distributive lattices is that they are graded (any two maximal chains have the same length), and the length of a maximal chain equals the number of meet-irreducible elements of the lattice.[22] The antimatroid representing a finite join-distributive lattice can be recovered from the lattice: the elements of the antimatroid can be taken to be the meet-irreducible elements of the lattice, and the feasible set corresponding to any element of the lattice consists of the set of meet-irreducible elements such that is not greater than or equal to in the lattice.
This representation of any finite join-distributive lattice as an accessible family of sets closed under unions (that is, as an antimatroid) may be viewed as an analogue of Birkhoff's representation theorem under which any finite distributive lattice has a representation as a family of sets closed under unions and intersections.
Supersolvable antimatroids edit
Motivated by a problem of defining partial orders on the elements of a Coxeter group, Armstrong (2009) studied antimatroids which are also supersolvable lattices. A supersolvable antimatroid is defined by a totally ordered collection of elements, and a family of sets of these elements. The family must include the empty set. Additionally, it must have the property that if two sets and belong to the family, if the set-theoretic difference is nonempty, and if is the smallest element of , then also belongs to the family. As Armstrong observes, any family of sets of this type forms an antimatroid. Armstrong also provides a lattice-theoretic characterization of the antimatroids that this construction can form.[23]
Join operation and convex dimension edit
If and are two antimatroids, both described as a family of sets over the same universe of elements, then another antimatroid, the join of and , can be formed as follows:
Joins are closely related to a closure operation that maps formal languages to antimatroids, where the closure of a language is the intersection of all antimatroids containing as a sublanguage. This closure has as its feasible sets the unions of prefixes of strings in . In terms of this closure operation, the join is the closure of the union of the languages of and . Every antimatroid can be represented as a join of a family of chain antimatroids, or equivalently as the closure of a set of basic words; the convex dimension of an antimatroid is the minimum number of chain antimatroids (or equivalently the minimum number of basic words) in such a representation. If is a family of chain antimatroids whose basic words all belong to , then generates if and only if the feasible sets of include all paths of . The paths of belonging to a single chain antimatroid must form a chain in the path poset of , so the convex dimension of an antimatroid equals the minimum number of chains needed to cover the path poset, which by Dilworth's theorem equals the width of the path poset.[25]
If one has a representation of an antimatroid as the closure of a set of basic words, then this representation can be used to map the feasible sets of the antimatroid to points in -dimensional Euclidean space: assign one coordinate per basic word , and make the coordinate value of a feasible set be the length of the longest prefix of that is a subset of . With this embedding, is a subset of another feasible set if and only if the coordinates for are all less than or equal to the corresponding coordinates of . Therefore, the order dimension of the inclusion ordering of the feasible sets is at most equal to the convex dimension of the antimatroid.[26] However, in general these two dimensions may be very different: there exist antimatroids with order dimension three but with arbitrarily large convex dimension.[27]
Enumeration edit
The number of possible antimatroids on a set of elements grows rapidly with the number of elements in the set. For sets of one, two, three, etc. elements, the number of distinct antimatroids is[28]
Applications edit
Both the precedence and release time constraints in the standard notation for theoretic scheduling problems may be modeled by antimatroids. Boyd & Faigle (1990) use antimatroids to generalize a greedy algorithm of Eugene Lawler for optimally solving single-processor scheduling problems with precedence constraints in which the goal is to minimize the maximum penalty incurred by the late scheduling of a task.
Glasserman & Yao (1994) use antimatroids to model the ordering of events in discrete event simulation systems.
Parmar (2003) uses antimatroids to model progress towards a goal in artificial intelligence planning problems.
In Optimality Theory, a mathematical model for the development of natural language based on optimization under constraints, grammars are logically equivalent to antimatroids.[29]
In mathematical psychology, antimatroids have been used to describe feasible states of knowledge of a human learner. Each element of the antimatroid represents a concept that is to be understood by the learner, or a class of problems that he or she might be able to solve correctly, and the sets of elements that form the antimatroid represent possible sets of concepts that could be understood by a single person. The axioms defining an antimatroid may be phrased informally as stating that learning one concept can never prevent the learner from learning another concept, and that any feasible state of knowledge can be reached by learning a single concept at a time. The task of a knowledge assessment system is to infer the set of concepts known by a given learner by analyzing his or her responses to a small and well-chosen set of problems. In this context antimatroids have also been called "learning spaces" and "well-graded knowledge spaces".[30]
Notes edit
- ^ See Korte, Lovász & Schrader (1991) for a comprehensive survey of antimatroid theory with many additional references.
- ^ Two early references are Edelman (1980) and Jamison (1980); Jamison was the first to use the term "antimatroid". Monjardet (1985) surveys the history of rediscovery of antimatroids.
- ^ See e.g. Kempner & Levit (2003), Definition 2.1 and Proposition 2.3, p. 2.
- ^ Korte, Lovász & Schrader (1991), p. 22.
- ^ a b Korte, Lovász & Schrader (1991), p. 5.
- ^ Korte, Lovász & Schrader (1991), Theorem 1.4, p. 24.
- ^ a b c Gordon (1997).
- ^ Korte, Lovász & Schrader (1991), pp. 24–25.
- ^ Gordon (1997) describes several results related to antimatroids of this type, but these antimatroids were mentioned earlier e.g. by Korte, Lovász & Schrader (1991). Chandran et al. (2003) use the connection to antimatroids as part of an algorithm for efficiently listing all perfect elimination orderings of a given chordal graph.
- ^ Björner, Lovász & Shor (1991); Knauer (2009).
- ^ a b c Korte, Lovász & Schrader (1991), Lemma 3.12, p. 31.
- ^ Korte, Lovász & Schrader (1991), p. 31.
- ^ Korte, Lovász & Schrader (1991), pp. 39–43.
- ^ See Korte, Lovász & Schrader (1991), Theorem 3.13, p. 32, which defines paths as rooted sets, sets with a distinguished element, and states an equivalent characterization on the families of rooted sets that form the paths of antimatroids.
- ^ Korte, Lovász & Schrader (1991), pp. 6, 22.
- ^ See Korte, Lovász & Schrader (1991), p. 22: "any word in an antimatroid can be extended to a basic word".
- ^ a b Korte, Lovász & Schrader (1991), Theorem 1.1, p. 21.
- ^ a b Korte, Lovász & Schrader (1991), p. 20.
- ^ Farber & Jamison (1986).
- ^ Adaricheva, Gorbunov & Tumanov (2003), Theorems 1.7 and 1.9; Armstrong (2009), Theorem 2.7.
- ^ Edelman (1980), Theorem 3.3; Armstrong (2009), Theorem 2.8.
- ^ Monjardet (1985) credits a dual form of this characterization to several papers from the 1960s by S. P. Avann.
- ^ Armstrong (2009).
- ^ Korte, Lovász & Schrader (1991), p. 42; Eppstein (2008), Section 7.2; Falmagne et al. (2013), section 14.4.
- ^ Edelman & Saks (1988); Korte, Lovász & Schrader (1991), Theorem 6.9.
- ^ Korte, Lovász & Schrader (1991), Corollary 6.10.
- ^ Eppstein (2008), Figure 15.
- ^ Sloane, N. J. A. (ed.), "Sequence A119770", The On-Line Encyclopedia of Integer Sequences, OEIS Foundation
- ^ Merchant & Riggle (2016).
- ^ Doignon & Falmagne (1999).
References edit
- Adaricheva, K. V.; Gorbunov, V. A.; Tumanov, V. I. (2003), "Join-semidistributive lattices and convex geometries", Advances in Mathematics, 173 (1): 1–49, doi:10.1016/S0001-8708(02)00011-7.
- Armstrong, Drew (2009), "The sorting order on a Coxeter group", Journal of Combinatorial Theory, Series A, 116 (8): 1285–1305, arXiv:0712.1047, doi:10.1016/j.jcta.2009.03.009, MR 2568800, S2CID 15474840.
- Birkhoff, Garrett; Bennett, M. K. (1985), "The convexity lattice of a poset", Order, 2 (3): 223–242, doi:10.1007/BF00333128, S2CID 118907732
- Björner, Anders; Lovász, László; Shor, Peter W. (1991), "Chip-firing games on graphs", European Journal of Combinatorics, 12 (4): 283–291, doi:10.1016/S0195-6698(13)80111-4, MR 1120415
- Björner, Anders; Ziegler, Günter M. (1992), "Introduction to greedoids", in White, Neil (ed.), Matroid Applications, Encyclopedia of Mathematics and its Applications, vol. 40, Cambridge: Cambridge University Press, pp. 284–357, doi:10.1017/CBO9780511662041.009, ISBN 0-521-38165-7, MR 1165537
- Boyd, E. Andrew; Faigle, Ulrich (1990), "An algorithmic characterization of antimatroids", Discrete Applied Mathematics, 28 (3): 197–205, doi:10.1016/0166-218X(90)90002-T, hdl:1911/101636.
- Chandran, L. S.; Ibarra, L.; Ruskey, F.; Sawada, J. (2003), "Generating and characterizing the perfect elimination orderings of a chordal graph" (PDF), Theoretical Computer Science, 307 (2): 303–317, doi:10.1016/S0304-3975(03)00221-4
- Dilworth, Robert P. (1940), "Lattices with unique irreducible decompositions", Annals of Mathematics, 41 (4): 771–777, doi:10.2307/1968857, JSTOR 1968857.
- Doignon, Jean-Paul; Falmagne, Jean-Claude (1999), Knowledge Spaces, Springer-Verlag, ISBN 3-540-64501-2.
- Edelman, Paul H. (1980), "Meet-distributive lattices and the anti-exchange closure", Algebra Universalis, 10 (1): 290–299, doi:10.1007/BF02482912, S2CID 120403229.
- Edelman, Paul H.; Saks, Michael E. (1988), "Combinatorial representation and convex dimension of convex geometries", Order, 5 (1): 23–32, doi:10.1007/BF00143895, S2CID 119826035.
- Eppstein, David (2008), Learning sequences, arXiv:0803.4030. Partially adapted as Chapters 13 and 14 of Falmagne, Jean-Claude; Albert, Dietrich; Doble, Chris; Eppstein, David; Hu, Xiangen, eds. (2013), Knowledge Spaces: Applications in Education, Springer-Verlag, doi:10.1007/978-3-642-35329-1, ISBN 978-3-642-35328-4.
- Farber, Martin; Jamison, Robert E. (1986), "Convexity in graphs and hypergraphs", SIAM Journal on Algebraic and Discrete Methods, 7 (3): 433–444, doi:10.1137/0607049, hdl:10338.dmlcz/127659, MR 0844046.
- Glasserman, Paul; Yao, David D. (1994), Monotone Structure in Discrete Event Systems, Wiley Series in Probability and Statistics, Wiley Interscience, ISBN 978-0-471-58041-6.
- Gordon, Gary (1997), "A β invariant for greedoids and antimatroids", Electronic Journal of Combinatorics, 4 (1): Research Paper 13, doi:10.37236/1298, MR 1445628.
- Jamison, Robert (1980), "Copoints in antimatroids", Proceedings of the Eleventh Southeastern Conference on Combinatorics, Graph Theory and Computing (Florida Atlantic Univ., Boca Raton, Fla., 1980), Vol. II, Congressus Numerantium, vol. 29, pp. 535–544, MR 0608454.
- Kempner, Yulia; Levit, Vadim E. (2003), "Correspondence between two antimatroid algorithmic characterizations", Electronic Journal of Combinatorics, 10: Research Paper 44, arXiv:math/0307013, Bibcode:2003math......7013K, doi:10.37236/1737, MR 2014531, S2CID 11015967
- Knauer, Kolja (2009), "Chip-firing, antimatroids, and polyhedra", European Conference on Combinatorics, Graph Theory and Applications (EuroComb 2009), Electronic Notes in Discrete Mathematics, vol. 34, pp. 9–13, doi:10.1016/j.endm.2009.07.002, MR 2591410
- Korte, Bernhard; Lovász, László; Schrader, Rainer (1991), Greedoids, Springer-Verlag, pp. 19–43, ISBN 3-540-18190-3.
- Merchant, Nazarré; Riggle, Jason (2016), "OT grammars, beyond partial orders: ERC sets and antimatroids", Natural Language & Linguistic Theory, 34: 241–269, doi:10.1007/s11049-015-9297-5, S2CID 170567540.
- Monjardet, Bernard (1985), "A use for frequently rediscovering a concept", Order, 1 (4): 415–417, doi:10.1007/BF00582748, S2CID 119378521.
- Parmar, Aarati (2003), "Some Mathematical Structures Underlying Efficient Planning", AAAI Spring Symposium on Logical Formalization of Commonsense Reasoning (PDF).


