
Summary
In graph theory, a branch of mathematics, a cluster graph is a graph formed from the disjoint union of complete graphs. Equivalently, a graph is a cluster graph if and only if it has no three-vertex induced path; for this reason, the cluster graphs are also called P3-free graphs. They are the complement graphs of the complete multipartite graphs[1] and the 2-leaf powers.[2] The cluster graphs are transitively closed, and every transitively closed undirected graph is a cluster graph.[3]
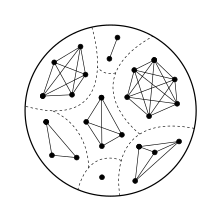
The cluster graphs are the graphs for which adjacency is an equivalence relation, and their connected components are the equivalence classes for this relation.
Related graph classes
editEvery cluster graph is a block graph, a cograph, and a claw-free graph.[1] Every maximal independent set in a cluster graph chooses a single vertex from each cluster, so the size of such a set always equals the number of clusters; because all maximal independent sets have the same size, cluster graphs are well-covered. The Turán graphs are complement graphs of cluster graphs, with all complete subgraphs of equal or nearly-equal size. The locally clustered graph (graphs in which every neighborhood is a cluster graph) are the diamond-free graphs, another family of graphs that contains the cluster graphs.
When a cluster graph is formed from cliques that are all the same size, the overall graph is a homogeneous graph, meaning that every isomorphism between two of its induced subgraphs can be extended to an automorphism of the whole graph. With only two exceptions, the cluster graphs and their complements are the only finite homogeneous graphs,[4] and infinite cluster graphs also form one of only a small number of different types of countably infinite homogeneous graphs.[5]
Computational problems
editA subcoloring of a graph is a partition of its vertices into induced cluster graphs. Thus, the cluster graphs are exactly the graphs of subchromatic number 1.[6]
The computational problem of finding a small set of edges to add or remove from a graph to transform it into a cluster graph is called cluster editing. It is NP-complete[7] but fixed-parameter tractable.[8]
Given a complete graph with edge costs (positive and negative) the clique partitioning problem asks for a subgraph that is a cluster graph such that the sum of the costs of the edges of the cluster graph is minimal.[9] This problem is closely related to the correlation clustering problem.
References
edit- ^ a b Cluster graphs, Information System on Graph Classes and their Inclusions, accessed 2016-06-26.
- ^ Nishimura, N.; Ragde, P.; Thilikos, D.M. (2002), "On graph powers for leaf-labeled trees", Journal of Algorithms, 42: 69–108, doi:10.1006/jagm.2001.1195.
- ^ McColl, W. F.; Noshita, K. (1986), "On the number of edges in the transitive closure of a graph", Discrete Applied Mathematics, 15 (1): 67–73, doi:10.1016/0166-218X(86)90020-X, MR 0856101
- ^ Gardiner, A. (1976), "Homogeneous graphs", Journal of Combinatorial Theory, Series B, 20 (1): 94–102, doi:10.1016/0095-8956(76)90072-1, MR 0419293.
- ^ Lachlan, A. H.; Woodrow, Robert E. (1980), "Countable ultrahomogeneous undirected graphs", Transactions of the American Mathematical Society, 262 (1): 51–94, doi:10.2307/1999974, MR 0583847.
- ^ Albertson, M. O.; Jamison, R. E.; Hedetniemi, S. T.; Locke, S. C. (1989), "The subchromatic number of a graph", Discrete Mathematics, 74 (1–2): 33–49, doi:10.1016/0012-365X(89)90196-9.
- ^ Shamir, Ron; Sharan, Roded; Tsur, Dekel (2004), "Cluster graph modification problems", Discrete Applied Mathematics, 144 (1–2): 173–182, doi:10.1016/j.dam.2004.01.007, MR 2095392.
- ^ Böcker, Sebastian; Baumbach, Jan (2013), "Cluster editing", The nature of computation, Lecture Notes in Comput. Sci., vol. 7921, Springer, Heidelberg, pp. 33–44, doi:10.1007/978-3-642-39053-1_5, MR 3102002.
- ^ Grötschel, Martin; Wakabayashi, Yoshiko (1989), A cutting plane algorithm for a clustering problem, Mathematical Programming, vol. 45, Springer, pp. 59–96, doi:10.1007/BF01589097.


