
Summary
In graph theory, a branch of mathematics, the disjoint union of graphs is an operation that combines two or more graphs to form a larger graph. It is analogous to the disjoint union of sets, and is constructed by making the vertex set of the result be the disjoint union of the vertex sets of the given graphs, and by making the edge set of the result be the disjoint union of the edge sets of the given graphs. Any disjoint union of two or more nonempty graphs is necessarily disconnected.
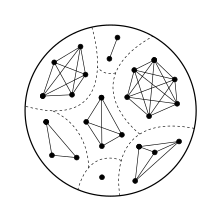
Notation edit
The disjoint union is also called the graph sum, and may be represented either by a plus sign or a circled plus sign: If and are two graphs, then or denotes their disjoint union.[1]
Related graph classes edit
Certain special classes of graphs may be represented using disjoint union operations. In particular:
- The forests are the disjoint unions of trees.[2]
- The cluster graphs are the disjoint unions of complete graphs.[3]
- The 2-regular graphs are the disjoint unions of cycle graphs.[4]
More generally, every graph is the disjoint union of connected graphs, its connected components.
The cographs are the graphs that can be constructed from single-vertex graphs by a combination of disjoint union and complement operations.[5]
References edit
- ^ Rosen, Kenneth H. (1999), Handbook of Discrete and Combinatorial Mathematics, Discrete Mathematics and Its Applications, CRC Press, p. 515, ISBN 9780849301490
- ^ Grossman, Jerrold W. (1990), Discrete Mathematics: An Introduction to Concepts, Methods, and Applications, Macmillan, p. 627, ISBN 9780023483318
- ^ Cluster graphs, Information System on Graph Classes and their Inclusions, accessed 2016-06-26.
- ^ Chartrand, Gary; Zhang, Ping (2013), A First Course in Graph Theory, Dover Books on Mathematics, Courier Corporation, p. 201, ISBN 9780486297309
- ^ Corneil, D. G.; Lerchs, H.; Stewart Burlingham, L. (1981), "Complement reducible graphs", Discrete Applied Mathematics, 3 (3): 163–174, doi:10.1016/0166-218X(81)90013-5, MR 0619603


