
Summary
In the mathematical field of graph theory, the diamond graph is a planar, undirected graph with 4 vertices and 5 edges.[1][2] It consists of a complete graph minus one edge.
| Diamond graph | |
|---|---|
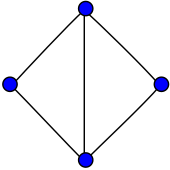 | |
| Vertices | 4 |
| Edges | 5 |
| Radius | 1 |
| Diameter | 2 |
| Girth | 3 |
| Automorphisms | 4 (Klein four-group: |
| Chromatic number | 3 |
| Chromatic index | 3 |
| Properties | Hamiltonian Planar Unit distance |
| Table of graphs and parameters | |
The diamond graph has radius 1, diameter 2, girth 3, chromatic number 3 and chromatic index 3. It is also a 2-vertex-connected and a 2-edge-connected, graceful,[3] Hamiltonian graph.
Diamond-free graphs and forbidden minor edit
A graph is diamond-free if it has no diamond as an induced subgraph. The triangle-free graphs are diamond-free graphs, since every diamond contains a triangle. The diamond-free graphs are locally clustered: that is, they are the graphs in which every neighborhood is a cluster graph. Alternatively, a graph is diamond-free if and only if every pair of maximal cliques in the graph shares at most one vertex.
The family of graphs in which each connected component is a cactus graph is downwardly closed under graph minor operations. This graph family may be characterized by a single forbidden minor. This minor is the diamond graph.[4]
If both the butterfly graph and the diamond graph are forbidden minors, the family of graphs obtained is the family of pseudoforests.
Algebraic properties edit
The full automorphism group of the diamond graph is a group of order 4 isomorphic to the Klein four-group, the direct product of the cyclic group with itself.
The characteristic polynomial of the diamond graph is . It is the only graph with this characteristic polynomial, making it a graph determined by its spectrum.
See also edit
References edit
- ^ Weisstein, Eric W. "Diamond Graph". MathWorld.
- ^ ISGCI: Information System on Graph Classes and their Inclusions "List of Small Graphs".
- ^ Sin-Min Lee, Y.C. Pan and Ming-Chen Tsai. "On Vertex-graceful (p,p+l)-Graphs". [1] Archived 2008-08-07 at the Wayback Machine
- ^ El-Mallah, Ehab; Colbourn, Charles J. (1988), "The complexity of some edge deletion problems", IEEE Transactions on Circuits and Systems, 35 (3): 354–362, doi:10.1109/31.1748.




