
Summary
In geometry, a golden rhombus is a rhombus whose diagonals are in the golden ratio:[1]
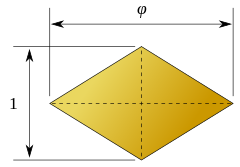
Equivalently, it is the Varignon parallelogram formed from the edge midpoints of a golden rectangle.[1] Rhombi with this shape form the faces of several notable polyhedra. The golden rhombus should be distinguished from the two rhombi of the Penrose tiling, which are both related in other ways to the golden ratio but have different shapes than the golden rhombus.[2]
Angles
edit(See the characterizations and the basic properties of the general rhombus for angle properties.)
The internal supplementary angles of the golden rhombus are:[3]
- Acute angle: ;
- by using the arctangent addition formula (see inverse trigonometric functions):
- Obtuse angle:
- which is also the dihedral angle of the dodecahedron.[4]
- Note: an "anecdotal" equality:
Edge and diagonals
editBy using the parallelogram law (see the basic properties of the general rhombus):[5]
The edge length of the golden rhombus in terms of the diagonal length is:
- Hence:
The diagonal lengths of the golden rhombus in terms of the edge length are:[3]
Area
edit- The area of the golden rhombus in terms of its diagonal length is:[6]
Note: , hence:
As the faces of polyhedra
editSeveral notable polyhedra have golden rhombi as their faces. They include the two golden rhombohedra (with six faces each), the Bilinski dodecahedron (with 12 faces), the rhombic icosahedron (with 20 faces), the rhombic triacontahedron (with 30 faces), and the nonconvex rhombic hexecontahedron (with 60 faces). The first five of these are the only convex polyhedra with golden rhomb faces, but there exist infinitely many nonconvex polyhedra having this shape for all of their faces.[7]
See also
editReferences
edit- ^ a b Senechal, Marjorie (2006), "Donald and the golden rhombohedra", in Davis, Chandler; Ellers, Erich W. (eds.), The Coxeter Legacy, American Mathematical Society, Providence, RI, pp. 159–177, ISBN 0-8218-3722-2, MR 2209027
- ^ For instance, an incorrect identification between the golden rhombus and one of the Penrose rhombi can be found in Livio, Mario (2002), The Golden Ratio: The Story of Phi, the World's Most Astonishing Number, New York: Broadway Books, p. 206
- ^ a b c Ogawa, Tohru (January 1987), "Symmetry of three-dimensional quasicrystals", Materials Science Forum, 22–24: 187–200, doi:10.4028/www.scientific.net/msf.22-24.187, S2CID 137677876. See in particular table 1, p. 188.
- ^ Gevay, G. (June 1993), "Non-metallic quasicrystals: Hypothesis or reality?", Phase Transitions, 44 (1–3): 47–50, Bibcode:1993PhaTr..44...47G, doi:10.1080/01411599308210255
- ^ Weisstein, Eric W. "Rhombus". MathWorld.
- ^ a b Weisstein, Eric W. "Golden Rhombus". MathWorld.
- ^ Grünbaum, Branko (2010), "The Bilinski dodecahedron and assorted parallelohedra, zonohedra, monohedra, isozonohedra, and otherhedra" (PDF), The Mathematical Intelligencer, 32 (4): 5–15, doi:10.1007/s00283-010-9138-7, hdl:1773/15593, MR 2747698, S2CID 120403108, archived from the original (PDF) on 2015-04-02.



