
Summary
A nautical mile is a unit of length used in air, marine, and space navigation, and for the definition of territorial waters.[2][3][4] Historically, it was defined as the meridian arc length corresponding to one minute (1/60 of a degree) of latitude at the equator, so that Earth's polar circumference is very near to 21,600 nautical miles (that is 60 minutes × 360 degrees). Today the international nautical mile is defined as 1,852 metres (about 6,076 ft; 1.151 mi).[5] The derived unit of speed is the knot, one nautical mile per hour.
| Nautical mile | |
|---|---|
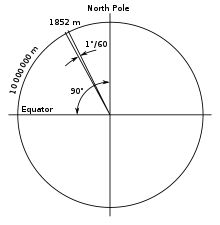 Historical definition – 1 nautical mile | |
| General information | |
| Unit of | length |
| Symbol | M, NM,[a] or nmi |
| Conversions | |
| 1 M, NM,[a] or nmi in ... | ... is equal to ... |
| metre | 1,852[1] |
| foot | ≈ 6,076 |
| statute mile | ≈ 1.151 |
| cable | 10 |
Unit symbol edit
There is no single internationally agreed symbol, with several symbols in use.[1]
- NM is used by the International Civil Aviation Organization.[6][7]
- nmi is used by the Institute of Electrical and Electronics Engineers[8] and the United States Government Publishing Office.[9]
- M is used as the abbreviation for the nautical mile by the International Hydrographic Organization.[10]
- nm is a non-standard abbreviation used in many maritime applications and texts, including U.S. Government Coast Pilots and Sailing Directions.[11] It conflicts with the SI symbol for nanometre.
History edit
The word mile is from the Latin phrase for a thousand paces: mille passus. Navigation at sea was done by eye[12] until around 1500 when navigational instruments were developed and cartographers began using a coordinate system with parallels of latitude and meridians of longitude.
The earliest reference of 60 miles to a degree is a map by Nicolaus Germanus in a 1482 edition of Geography (Ptolemy) indicating one degree of longitude at the Equator contained "milaria 60".[13] An earlier manuscript map by Nicolaus Germanus in a previous edition of Geography (Ptolemy) stated "unul gradul log. et latitud sub equinortiali formet stadia 500 que fanut miliaria 62-1/2" (one degree longitude and latitude under the equator forms 500 stadia, which make 62-1/2 miles).[14] Whether a correction or convenience, the reason for the change from 62-1/2 to 60 miles to a degree is not explained. Eventually, the ratio of 60 miles to a degree appeared in English in a 1555 translation of Pietro Martire d'Anghiera's Decades: "[Ptolemy] assigned likewise to every degree three score miles."[15]
By the late 16th century English geographers and navigators knew that the ratio of distances at sea to degrees was constant along any great circle (such as the equator, or any meridian), assuming that Earth was a sphere. In 1574, William Bourne (mathematician) stated in A Regiment for the Sea the "rule to raise a degree" practised by navigators: "But as I take it, we in England should allowe 60 myles to one degrée: that is, after 3 miles to one of our Englishe leagues, wherefore 20 of oure English leagues shoulde answere to one degrée."[16] Likewise, Robert Hues wrote in 1594 that the distance along a great circle was 60 miles per degree.[17] However, these referred to the old English mile of 5000 feet and league of 15,000 feet, relying upon Ptolemy's underestimate of the Earth's circumference.[18] In the early seventeenth century, English geographers started to acknowledge the discrepancy between the angular measurement of a degree of latitude and the linear measurement of miles. In 1624 Edmund Gunter suggested 352,000 feet to a degree (5866 2/3 feet per arcminute).[19][17] In 1633, William Oughtred suggested 349,800 feet to a degree (5830 feet per arcminute).[20] Both Gunter and Oughtred put forward the notion of dividing a degree into 100 parts, but their proposal was generally ignored by navigators. The ratio of 60 miles, or 20 leagues, to a degree of latitude remained fixed while the length of the mile was revised with better estimates of the earth’s circumference. In 1637, Robert Norwood proposed a new measurement of 6120 feet for an arcminute of latitude, which was within 44 feet of the currently accepted value for a nautical mile.[21]
Since the Earth is not a perfect sphere but is an oblate spheroid with slightly flattened poles, a minute of latitude is not constant, but about 1,861 metres at the poles and 1,843 metres at the Equator.[22] France and other metric countries state that in principle a nautical mile is an arcminute of a meridian at a latitude of 45°, but that is a modern justification for a more mundane calculation that was developed a century earlier. By the mid-19th century, France had defined a nautical mile via the original 1791 definition of the metre, one ten-millionth of a quarter meridian.[23][24] So 10,000,000 m/90 × 60 = 1,851.85 m ≈ 1,852 m became the metric length for a nautical mile. France made it legal for the French Navy in 1906, and many metric countries voted to sanction it for international use at the 1929 International Hydrographic Conference.[citation needed]
Both the United States and the United Kingdom used an average arcminute—specifically, a minute of arc of a great circle of a sphere having the same surface area as the Clarke 1866 ellipsoid.[25] The authalic (equal area) radius of the Clarke 1866 ellipsoid is 6,370,997.2 metres (20,902,222 ft).[26] The resulting arcminute is 1,853.2480 metres (6,080.210 ft). The United States chose five significant digits for its nautical mile, 6,080.2 feet, whereas the United Kingdom chose four significant digits for its Admiralty mile, 6,080 feet.
In 1929 the international nautical mile was defined by the First International Extraordinary Hydrographic Conference in Monaco as exactly 1,852 metres (which is 6,076.12 ft).[1] The United States did not adopt the international nautical mile until 1954.[27] Britain adopted it in 1970,[28] but legal references to the obsolete unit are now converted to 1,853 metres (which is 6,079.40 ft).[29]
Similar definitions edit
The metre was originally defined as 1⁄10,000,000 of the length of the meridian arc from the North pole to the equator (1% of a centesimal degree of latitude), [b] thus one kilometre of distance corresponds to one centigrad (also known as centesimal arc minute) of latitude. The Earth's circumference is therefore approximately 40,000 km. The equatorial circumference is slightly longer than the polar circumference – the measurement based on this (40,075.017 km/360 × 60 = 1,855.3 metres) is known as the geographical mile.
Using the definition 1/60 of a degree of latitude on Mars, a Martian nautical mile equals to 983 m (1,075 yd). This is potentially useful for celestial navigation on a human mission to the planet, both as a shorthand and a quick way to roughly determine the location.[31]
See also edit
Notes edit
- ^ Alternative meanings of the abbreviation "nm" or "NM" are listed here.
- ^ No meridian was specified in either 1791, 1793, 1795 or 1799 . For example, the Law of 18 Germinal an III (April 7, 1795) states: "Meter, the measure of length equal to the ten-millionth part of a terrestrial meridian contained between the north pole and the equator."[30]
References edit
- ^ a b c Göbel, E.; Mills, I.M.; Wallard, Andrew, eds. (2006). The International System of Units (SI) (PDF) (8th ed.). Paris: Bureau International des Poids et Mesures. p. 127. ISBN 92-822-2213-6. Archived from the original (PDF) on 2017-08-14. Retrieved 2017-06-20.
- ^ Wragg, David W. (1973). A Dictionary of Aviation (first ed.). Osprey. p. 200. ISBN 9780850451634.
- ^ "mile | unit of measurement". Encyclopædia Britannica. Archived from the original on 2022-10-25. Retrieved 2016-06-10.
- ^ "UNITED NATIONS CONVENTION ON THE LAW OF THE SEA". www.un.org. Archived from the original on 2017-12-18. Retrieved 2016-06-10.
- ^ Wragg, David W. (1973). A Dictionary of Aviation (first ed.). Osprey. p. 200. ISBN 9780850451634.
- ^ "WS SIGMET Quick Reference Guide" (PDF). ICAO. Archived (PDF) from the original on 2020-11-21. Retrieved 2016-06-09.
- ^ International Standards and Recommended Practices, Annex 5 to the Convention on International Civil Aviation, “Units of measurement to be Used in Air and Ground Operations”, ICAO, Fifth Edition, July 2010.
- ^ "APPENDIX A: SYMBOLS AND PREFIXES". IEEE. Archived from the original on 2021-04-23. Retrieved 2016-06-09.
- ^ "U.S. Government Printing Office Style Manual". U.S. Government Printing Office. Archived from the original on 2018-11-19. Retrieved 2016-06-10.
- ^ Symboles, Abréviations et Termes utilisés sur les cartes marines [Symbols, Abbreviations and Terms used on Charts] (PDF) (in French and English). Vol. 1D (INT1) (6th ed.). Service Hydrographique et Océanographique de la Marine (SHOM). 2016. Archived from the original (PDF) on 2016-08-21. Retrieved 2018-01-04. also available as Symbols and Abbreviations used on ADMIRALTY Paper Charts. Vol. NP5011 (6th ed.). United Kingdom Hydrographic Office. 2016. section B, line 45. ISBN 978-0-70-774-1741.
- ^ Dutton's Navigation and Piloting (14th ed.). Annapolis, MD: Naval Institute Press. 1985. ISBN 0-87021-157-9.
- ^ "Mile, Nautical and Statute – FREE Mile, Nautical and Statute information | Encyclopedia.com: Find Mile, Nautical and Statute research". www.encyclopedia.com. Archived from the original on 2016-06-07. Retrieved 2016-06-10.
- ^ Germanus, Nicolaus (1482). Ptolemy's Cosmographia. Ulm: Lienhart Holle. p. 245. Archived from the original on 23 October 2023. Retrieved 8 October 2023.
- ^ Germanus, Nicolaus (c. 1460). "Eleventh map of Asia," Ptolemy's Geographia. Archived from the original on 23 October 2023. Retrieved 8 October 2023.
- ^ Anghiera, Pietro Martire d' (1555). The Decades of the Newe Worlde Or West India. London: Guilielm. Powell. p. 323. Archived from the original on 2023-10-24. Retrieved 2023-10-08.
- ^ Bourne, William (1574). A regiment for the sea. London: Thomas Hacket. p. 39. Archived from the original on 23 October 2023. Retrieved 6 October 2023.
- ^ a b Waters, David W. (1958). The Art of Navigation in England in Elizabethan and Early Stuart Times. p. 374.
- ^ Hues, Robert (1659). A learned treatise of globes, both cœlestiall and terrestriall with their several uses. London: J.S. for Andrew Kemb. pp. 157, 163. Archived from the original on 24 October 2023. Retrieved 6 October 2023.
- ^ Gunther, Edmund (1673). The Works of Edmund Gunther. London: A. C.[larke]. for Francis Eglesfield, at the Marigold in St. Paul's Church-yard. pp. 280–281. Retrieved 6 October 2023.
- ^ Oughtred, William (1639). The Circles of Proportion and the Horizontall Instrument. London: The Circles of Proportion and the Horizontall Instrument. p. 27. Archived from the original on 24 October 2023. Retrieved 6 October 2023.
- ^ Norwood, Richard (1699). The Sea-man's Practice: Containing a Fundamental Problem in Navigation, Experimentally Verified. London: Richard Mount. p. 43. Archived from the original on 24 October 2023. Retrieved 6 October 2023.
- ^ McNish, Larry. "RASC Calgary Centre - Latitude and Longitude". The Royal Astronomical Society of Canada. Archived from the original on 30 August 2019. Retrieved 30 August 2019.
- ^ Bureau des Longitudes (1933). "Mesures employées sur les cartes marines". Annuaire Pour l'An 1933: 392. Archived from the original on 2019-08-31. Retrieved 2019-08-31.
The nautical mile [mille marin] is in principle the length of the sexagesimal minute of a meridian at a latitude of 45°. ... If we assume that the metre is exactly the ten-millionth part of the terrestrial quarter meridian, it would be equal to 1,851.85 m.
– Translation by Wikipedia. - ^ Bureau des Longitudes (1848). "Mesures itinéraires". Annuaire Pour l'An 1848: 74. Archived from the original on 2019-08-31. Retrieved 2019-08-31.
- ^ Blazebrook, Richard (1922), A Dictionary of Physics, vol. 1, Macmillan and Co, Limited, p. 587
- ^ Snyder, John P. (1987). Map Projections: A Working Manual. p. 16.
- ^ Astin, A.V.; Karo, H. Arnold (June 25, 1959). "Refinement of values for the yard and the pound" (PDF). NOAA.gov. National Bureau of Standards. Archived from the original (PDF) on March 9, 2013. Retrieved 2018-07-07.
- ^ "Nautical mile definition and meaning | Collins English Dictionary". Collins Dictionary. Archived from the original on 1 September 2019. Retrieved 1 September 2019.
- ^ "The Units of Measurement Regulations 1995". www.legislation.gov.uk. Archived from the original on 2017-03-24. Retrieved 2016-06-10.
- ^ Hallock, William; Wade, Herbert T. (1906), Outlines of the Evolution of Weights and Measures and the Metric System, New York The Macmillan company, p. 54
- ^ Zubrin, Robert (1996). The Case for Mars: The Plan to Settle the Red Planet and Why We Must. Richard Wagner. New York: Free Press. p. 162. ISBN 0-684-82757-3. OCLC 34906203.


