
Summary
In geometry, a sectrix of Maclaurin is defined as the curve swept out by the point of intersection of two lines which are each revolving at constant rates about different points called poles. Equivalently, a sectrix of Maclaurin can be defined as a curve whose equation in biangular coordinates is linear. The name is derived from the trisectrix of Maclaurin (named for Colin Maclaurin), which is a prominent member of the family, and their sectrix property, which means they can be used to divide an angle into a given number of equal parts. There are special cases known as arachnida or araneidans because of their spider-like shape, and Plateau curves after Joseph Plateau who studied them.
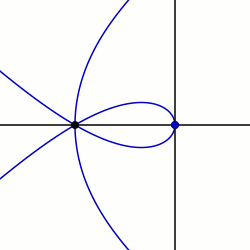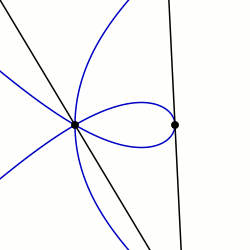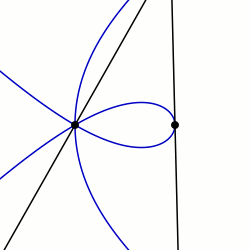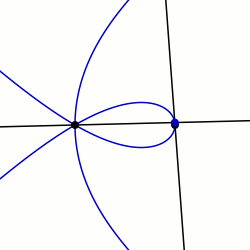
Equations in polar coordinates edit
We are given two lines rotating about two poles and . By translation and rotation we may assume and . At time , the line rotating about has angle and the line rotating about has angle , where , , and are constants. Eliminate to get where and . We assume is rational, otherwise the curve is not algebraic and is dense in the plane. Let be the point of intersection of the two lines and let be the angle at , so . If is the distance from to then, by the law of sines,
so
is the equation in polar coordinates.
The case and where is an integer greater than 2 gives arachnida or araneidan curves
The case and where is an integer greater than 1 gives alternate forms of arachnida or araneidan curves
A similar derivation to that above gives
as the polar equation (in and ) if the origin is shifted to the right by . Note that this is the earlier equation with a change of parameters; this to be expected from the fact that two poles are interchangeable in the construction of the curve.
Equations in the complex plane, rectangular coordinates and orthogonal trajectories edit
Let where and are integers and the fraction is in lowest terms. In the notation of the previous section, we have or . If then , so the equation becomes or . This can also be written
from which it is relatively simple to derive the Cartesian equation given m and n. The function is analytic so the orthogonal trajectories of the family are the curves , or
Parametric equations edit
Let where and are integers, and let where is a parameter. Then converting the polar equation above to parametric equations produces
- .
Applying the angle addition rule for sine produces
- .
So if the origin is shifted to the right by a/2 then the parametric equations are
- .
These are the equations for Plateau curves when , or
- .
Inversive triplets edit
The inverse with respect to the circle with radius a and center at the origin of
is
- .
This is another curve in the family. The inverse with respect to the other pole produces yet another curve in the same family and the two inverses are in turn inverses of each other. Therefore each curve in the family is a member of a triple, each of which belongs to the family and is an inverse of the other two. The values of q in this family are
- .
Sectrix properties edit
Let where and are integers in lowest terms and assume is constructible with compass and straightedge. (The value of is usually 0 in practice so this is not normally an issue.) Let be a given angle and suppose that the sectrix of Maclaurin has been drawn with poles and according to the construction above. Construct a ray from at angle and let be the point of intersection of the ray and the sectrix and draw . If is the angle of this line then
so . By repeatedly subtracting and from each other as in the Euclidean algorithm, the angle can be constructed. Thus, the curve is an m-sectrix, meaning that with the aid of the curve an arbitrary angle can be divided by any integer. This is a generalization of the concept of a trisectrix and examples of these will be found below.
Now draw a ray with angle from and be the point of intersection of this ray with the curve. The angle of is
and subtracting gives an angle of
- .
Applying the Euclidean Algorithm again gives an angle of showing that the curve is also an n-sectrix.
Finally, draw a ray from with angle and a ray from with angle , and let be the point of intersection. This point is on the perpendicular bisector of so there is a circle with center containing and . so any point on the circle forms an angle of between and . (This is, in fact, one of the Apollonian circles of P and P'.) Let be the point intersection of this circle and the curve. Then so
- .
Applying a Euclidean algorithm a third time gives an angle of , showing that the curve is an (m−n)-sectrix as well.
Specific cases edit
q = 0 edit
This is the curve
which is a line through .
q = 1 edit
This is a circle containing the origin and . It has polar equation
- .
It is the inverse with respect to the origin of the q = 0 case. The orthogonal trajectories of the family of circles is the family These form the Apollonian circles with poles and .
q = -1 edit
These curves have polar equation
- ,
complex equation In rectangular coordinates this becomes which is a conic. From the polar equation it is evident that the curves has asymptotes at and which are at right angles. So the conics are, in fact, rectangular hyperbolas. The center of the hyperbola is always . The orthogonal trajectories of this family are given by which is the family of Cassini ovals with foci and .
Trisectrix of Maclaurin edit
In the case where (or by switching the poles) and , the equation is
- .
This is the Trisectrix of Maclaurin which is specific case whose generalization is the sectrix of Maclaurin. The construction above gives a method that this curve may be used as a trisectrix.
Limaçon trisectrix and rose edit
In the case where (or by switching the poles) and , the equation is
- .
This is the Limaçon trisectrix.
The equation with the origin take to be the other pole is the rose curve that has the same shape
- .
The 3 in the numerator of q and the construction above give a method that the curve may be used as a trisectrix.
References edit
- "Sectrice de Maclaurin" at Encyclopédie des Formes Mathématiques Remarquables (In French)
- Weisstein, Eric W. "Arachnida". MathWorld.
- Weisstein, Eric W. "Plateau Curves". MathWorld.


