
Summary
In condensed matter physics, a spin glass is a magnetic state characterized by randomness, besides cooperative behavior in freezing of spins at a temperature called "freezing temperature" Tf.[1] In ferromagnetic solids, component atoms' magnetic spins all align in the same direction. Spin glass when contrasted with a ferromagnet is defined as "disordered" magnetic state in which spins are aligned randomly or without a regular pattern and the couplings too are random.[1]
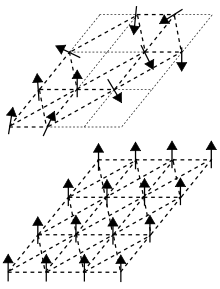

The term "glass" comes from an analogy between the magnetic disorder in a spin glass and the positional disorder of a conventional, chemical glass, e.g., a window glass. In window glass or any amorphous solid the atomic bond structure is highly irregular; in contrast, a crystal has a uniform pattern of atomic bonds. In ferromagnetic solids, magnetic spins all align in the same direction; this is analogous to a crystal's lattice-based structure.
The individual atomic bonds in a spin glass are a mixture of roughly equal numbers of ferromagnetic bonds (where neighbors have the same orientation) and antiferromagnetic bonds (where neighbors have exactly the opposite orientation: north and south poles are flipped 180 degrees). These patterns of aligned and misaligned atomic magnets create what are known as frustrated interactions – distortions in the geometry of atomic bonds compared to what would be seen in a regular, fully aligned solid. They may also create situations where more than one geometric arrangement of atoms is stable.
There are two main aspects of spin glass. On the physical side, spin glasses are real materials with distinctive properties, a review of which is.[2] On the mathematical side, simple statistical mechanics models, inspired by real spin glasses, are widely studied and applied.[3]
Spin glasses and the complex internal structures that arise within them are termed "metastable" because they are "stuck" in stable configurations other than the lowest-energy configuration (which would be aligned and ferromagnetic). The mathematical complexity of these structures is difficult but fruitful to study experimentally or in simulations; with applications to physics, chemistry, materials science and artificial neural networks in computer science.
Magnetic behavior
editIt is the time dependence which distinguishes spin glasses from other magnetic systems.
Above the spin glass transition temperature, Tc,[note 1] the spin glass exhibits typical magnetic behaviour (such as paramagnetism).
If a magnetic field is applied as the sample is cooled to the transition temperature, magnetization of the sample increases as described by the Curie law. Upon reaching Tc, the sample becomes a spin glass, and further cooling results in little change in magnetization. This is referred to as the field-cooled magnetization.
When the external magnetic field is removed, the magnetization of the spin glass falls rapidly to a lower value known as the remanent magnetization.
Magnetization then decays slowly as it approaches zero (or some small fraction of the original value – this remains unknown). This decay is non-exponential, and no simple function can fit the curve of magnetization versus time adequately.[4] This slow decay is particular to spin glasses. Experimental measurements on the order of days have shown continual changes above the noise level of instrumentation.[4]
Spin glasses differ from ferromagnetic materials by the fact that after the external magnetic field is removed from a ferromagnetic substance, the magnetization remains indefinitely at the remanent value. Paramagnetic materials differ from spin glasses by the fact that, after the external magnetic field is removed, the magnetization rapidly falls to zero, with no remanent magnetization. The decay is rapid and exponential.[citation needed]
If the sample is cooled below Tc in the absence of an external magnetic field, and a magnetic field is applied after the transition to the spin glass phase, there is a rapid initial increase to a value called the zero-field-cooled magnetization. A slow upward drift then occurs toward the field-cooled magnetization.
Surprisingly, the sum of the two complicated functions of time (the zero-field-cooled and remanent magnetizations) is a constant, namely the field-cooled value, and thus both share identical functional forms with time,[5] at least in the limit of very small external fields.
Edwards–Anderson model
editThis is similar to the Ising model. In this model, we have spins arranged on a -dimensional lattice with only nearest neighbor interactions. This model can be solved exactly for the critical temperatures and a glassy phase is observed to exist at low temperatures.[6] The Hamiltonian for this spin system is given by:
where refers to the Pauli spin matrix for the spin-half particle at lattice point , and the sum over refers to summing over neighboring lattice points and . A negative value of denotes an antiferromagnetic type interaction between spins at points and . The sum runs over all nearest neighbor positions on a lattice, of any dimension. The variables representing the magnetic nature of the spin-spin interactions are called bond or link variables.
In order to determine the partition function for this system, one needs to average the free energy where , over all possible values of . The distribution of values of is taken to be a Gaussian with a mean and a variance :
Solving for the free energy using the replica method, below a certain temperature, a new magnetic phase called the spin glass phase (or glassy phase) of the system is found to exist which is characterized by a vanishing magnetization along with a non-vanishing value of the two point correlation function between spins at the same lattice point but at two different replicas:
where are replica indices. The order parameter for the ferromagnetic to spin glass phase transition is therefore , and that for paramagnetic to spin glass is again . Hence the new set of order parameters describing the three magnetic phases consists of both and .
Under the assumption of replica symmetry, the mean-field free energy is given by the expression:[6]
Sherrington–Kirkpatrick model
editIn addition to unusual experimental properties, spin glasses are the subject of extensive theoretical and computational investigations. A substantial part of early theoretical work on spin glasses dealt with a form of mean-field theory based on a set of replicas of the partition function of the system.
An important, exactly solvable model of a spin glass was introduced by David Sherrington and Scott Kirkpatrick in 1975. It is an Ising model with long range frustrated ferro- as well as antiferromagnetic couplings. It corresponds to a mean-field approximation of spin glasses describing the slow dynamics of the magnetization and the complex non-ergodic equilibrium state.
Unlike the Edwards–Anderson (EA) model, in the system though only two-spin interactions are considered, the range of each interaction can be potentially infinite (of the order of the size of the lattice). Therefore, we see that any two spins can be linked with a ferromagnetic or an antiferromagnetic bond and the distribution of these is given exactly as in the case of Edwards–Anderson model. The Hamiltonian for SK model is very similar to the EA model:
where have same meanings as in the EA model. The equilibrium solution of the model, after some initial attempts by Sherrington, Kirkpatrick and others, was found by Giorgio Parisi in 1979 with the replica method. The subsequent work of interpretation of the Parisi solution—by M. Mezard, G. Parisi, M.A. Virasoro and many others—revealed the complex nature of a glassy low temperature phase characterized by ergodicity breaking, ultrametricity and non-selfaverageness. Further developments led to the creation of the cavity method, which allowed study of the low temperature phase without replicas. A rigorous proof of the Parisi solution has been provided in the work of Francesco Guerra and Michel Talagrand.[7]
Phase diagram
editWhen there is a uniform external magnetic field of magnitude , the energy function becomes Let all couplings are IID samples from the gaussian distribution of mean 0 and variance . In 1979, J.R.L. de Almeida and David Thouless[8] found that, as in the case of the Ising model, the mean-field solution to the SK model becomes unstable when under low-temperature, low-magnetic field state.
The stability region on the phase diagram of the SK model is determined by two dimensionless parameters . Its phase diagram has two parts, divided by the de Almeida-Thouless curve, The curve is the solution set to the equations[8] The phase transition occurs at . Just below it, we have At low temperature, high magnetic field limit, the line is
Infinite-range model
editThis is also called the "p-spin model".[3] The infinite-range model is a generalization of the Sherrington–Kirkpatrick model where we not only consider two-spin interactions but -spin interactions, where and is the total number of spins. Unlike the Edwards–Anderson model, but similar to the SK model, the interaction range is infinite. The Hamiltonian for this model is described by:
where have similar meanings as in the EA model. The limit of this model is known as the random energy model. In this limit, the probability of the spin glass existing in a particular state depends only on the energy of that state and not on the individual spin configurations in it. A Gaussian distribution of magnetic bonds across the lattice is assumed usually to solve this model. Any other distribution is expected to give the same result, as a consequence of the central limit theorem. The Gaussian distribution function, with mean and variance , is given as:
The order parameters for this system are given by the magnetization and the two point spin correlation between spins at the same site , in two different replicas, which are the same as for the SK model. This infinite range model can be solved explicitly for the free energy[6] in terms of and , under the assumption of replica symmetry as well as 1-Replica Symmetry Breaking.[6]
Non-ergodic behavior and applications
editA thermodynamic system is ergodic when, given any (equilibrium) instance of the system, it eventually visits every other possible (equilibrium) state (of the same energy). One characteristic of spin glass systems is that, below the freezing temperature , instances are trapped in a "non-ergodic" set of states: the system may fluctuate between several states, but cannot transition to other states of equivalent energy. Intuitively, one can say that the system cannot escape from deep minima of the hierarchically disordered energy landscape; the distances between minima are given by an ultrametric, with tall energy barriers between minima.[note 2] The participation ratio counts the number of states that are accessible from a given instance, that is, the number of states that participate in the ground state. The ergodic aspect of spin glass was instrumental in the awarding of half the 2021 Nobel Prize in Physics to Giorgio Parisi.[9][10][11]
For physical systems, such as dilute manganese in copper, the freezing temperature is typically as low as 30 kelvins (−240 °C), and so the spin-glass magnetism appears to be practically without applications in daily life. The non-ergodic states and rugged energy landscapes are, however, quite useful in understanding the behavior of certain neural networks, including Hopfield networks, as well as many problems in computer science optimization and genetics.
Spin-glass without structural disorder
editElemental crystalline neodymium is paramagnetic at room temperature and becomes an antiferromagnet with incommensurate order upon cooling below 19.9 K.[12] Below this transition temperature it exhibits a complex set of magnetic phases[13][14] that have long spin relaxation times and spin-glass behavior that does not rely on structural disorder.[15]
History
editA detailed account of the history of spin glasses from the early 1960s to the late 1980s can be found in a series of popular articles by Philip W. Anderson in Physics Today.[16][17][18][19][20][21][22][23]
Discovery
editIn 1930s, material scientists discovered the Kondo effect, where the resistivity of nominally pure gold reaches a minimum at 10 K, and similarly for nominally pure Cu at 2 K. It was later understood that the Kondo effect occurs when a nonmagnetic metal is infused with dilute magnetic atoms.
Unusual behavior was observed in of iron-in-gold alloy (AuFe) and manganese-in-copper alloy (CuMn) at around 1 to 10 atomic percent. Cannella and Mydosh observed in 1972[24] that AuFe had an unexpected cusplike peak in the a.c. susceptibility at a well defined temperature, which would later be termed spin glass freezing temperature.[25]
It was also called "mictomagnet" (micto- is Greek for "mixed"). The term arose from the observation that these materials often contain a mix of ferromagnetic ( ) and antiferromagnetic ( ) interactions, leading to their disordered magnetic structure. This term fell out of favor as the theoretical understanding of spin glasses evolved, recognizing that the magnetic frustration arises not just from a simple mixture of ferro- and antiferromagnetic interactions, but from their randomness and frustration in the system.
Sherrington-Kirkpatrick model
editSherrington and Kirkpatrick proposed the SK model in 1975, and solved it by the replica method.[26] They discovered that at low temperatures, its entropy becomes negative, which they thought was because the replica method is a heuristic method that does not apply at low temperatures.
It was then discovered that the replica method was correct, but the problem lies in that the low-temperature broken symmetry in the SK model cannot be purely characterized by the Edwards-Anderson order parameter. Instead, further order parameters are necessary, which leads to replica breaking ansatz of Giorgio Parisi. At the full replica breaking ansatz, infinitely many order parameters are required to characterize a stable solution.[27]
Applications
editThe formalism of replica mean-field theory has also been applied in the study of neural networks, where it has enabled calculations of properties such as the storage capacity of simple neural network architectures without requiring a training algorithm (such as backpropagation) to be designed or implemented.[28]
More realistic spin glass models with short range frustrated interactions and disorder, like the Gaussian model where the couplings between neighboring spins follow a Gaussian distribution, have been studied extensively as well, especially using Monte Carlo simulations. These models display spin glass phases bordered by sharp phase transitions.
Besides its relevance in condensed matter physics, spin glass theory has acquired a strongly interdisciplinary character, with applications to neural network theory, computer science, theoretical biology, econophysics etc.
Spin glass models were adapted to the folding funnel model of protein folding.
See also
editNotes
editReferences
edit- ^ a b Mydosh, J. A. (1993). Spin Glasses: An Experimental Introduction. London, Washington DC: Taylor & Francis. p. 3. ISBN 0748400389. 9780748400386.
- ^ Ford, Peter J. (March 1982). "Spin glasses". Contemporary Physics. 23 (2): 141–168. Bibcode:1982ConPh..23..141F. doi:10.1080/00107518208237073. ISSN 0010-7514.
- ^ a b Mézard, Marc; Montanari, Andrea (2009). Information, physics, and computation. Oxford graduate texts. Oxford: Oxford university press. ISBN 978-0-19-857083-7.
- ^ a b Joy, P. A.; Kumar, P. S. Anil; Date, S. K. (7 October 1998). "The relationship between field-cooled and zero-field-cooled susceptibilities of some ordered magnetic systems". J. Phys.: Condens. Matter. 10 (48): 11049–11054. Bibcode:1998JPCM...1011049J. doi:10.1088/0953-8984/10/48/024. S2CID 250734239.
- ^ Nordblad, P.; Lundgren, L.; Sandlund, L. (February 1986). "A link between the relaxation of the zero field cooled and the thermoremanent magnetizations in spin glasses". Journal of Magnetism and Magnetic Materials. 54–57 (1): 185–186. Bibcode:1986JMMM...54..185N. doi:10.1016/0304-8853(86)90543-3.
- ^ a b c d Nishimori, Hidetoshi (2001). Statistical Physics of Spin Glasses and Information Processing: An Introduction. Oxford: Oxford University Press. p. 243. ISBN 9780198509400.
- ^ Michel Talagrand, Mean Field Models for Spin Glasses Volume I: Basic Examples (2010)
- ^ a b Almeida, J R L de; Thouless, D J (May 1978). "Stability of the Sherrington-Kirkpatrick solution of a spin glass model". Journal of Physics A: Mathematical and General. 11 (5): 983–990. Bibcode:1978JPhA...11..983D. doi:10.1088/0305-4470/11/5/028. ISSN 0305-4470.
- ^ Geddes, Linda (2021-10-05). "Trio of scientists win Nobel prize for physics for climate work". The Guardian. Retrieved 2023-12-23.
- ^ "The Nobel Prize in Physics 2021 - Popular Science Background" (PDF). Retrieved 2023-12-23.
- ^ "Scientific Background for the Nobel Prize in Physics 2021" (PDF). Nobel Committee for Physics. 5 October 2021. Retrieved 3 November 2023.
- ^ Andrej Szytula; Janusz Leciejewicz (8 March 1994). Handbook of Crystal Structures and Magnetic Properties of Rare Earth Intermetallics. CRC Press. p. 1. ISBN 978-0-8493-4261-5.
- ^ Zochowski, S W; McEwen, K A; Fawcett, E (1991). "Magnetic phase diagrams of neodymium". Journal of Physics: Condensed Matter. 3 (41): 8079–8094. Bibcode:1991JPCM....3.8079Z. doi:10.1088/0953-8984/3/41/007. ISSN 0953-8984.
- ^ Lebech, B; Wolny, J; Moon, R M (1994). "Magnetic phase transitions in double hexagonal close packed neodymium metal-commensurate in two dimensions". Journal of Physics: Condensed Matter. 6 (27): 5201–5222. Bibcode:1994JPCM....6.5201L. doi:10.1088/0953-8984/6/27/029. ISSN 0953-8984.
- ^ Kamber, Umut; Bergman, Anders; Eich, Andreas; Iuşan, Diana; Steinbrecher, Manuel; Hauptmann, Nadine; Nordström, Lars; Katsnelson, Mikhail I.; Wegner, Daniel; Eriksson, Olle; Khajetoorians, Alexander A. (2020). "Self-induced spin glass state in elemental and crystalline neodymium". Science. 368 (6494). arXiv:1907.02295. doi:10.1126/science.aay6757. ISSN 0036-8075. PMID 32467362.
- ^ Philip W. Anderson (1988). "Spin Glass I: A Scaling Law Rescued" (PDF). Physics Today. 41 (1): 9–11. Bibcode:1988PhT....41a...9A. doi:10.1063/1.2811268.
- ^ Philip W. Anderson (1988). "Spin Glass II: Is There a Phase Transition?" (PDF). Physics Today. 41 (3): 9. Bibcode:1988PhT....41c...9A. doi:10.1063/1.2811336.
- ^ Philip W. Anderson (1988). "Spin Glass III: Theory Raises its Head" (PDF). Physics Today. 41 (6): 9–11. Bibcode:1988PhT....41f...9A. doi:10.1063/1.2811440.
- ^ Philip W. Anderson (1988). "Spin Glass IV: Glimmerings of Trouble" (PDF). Physics Today. 41 (9): 9–11. Bibcode:1988PhT....41i...9A. doi:10.1063/1.881135.
- ^ Philip W. Anderson (1989). "Spin Glass V: Real Power Brought to Bear" (PDF). Physics Today. 42 (7): 9–11. Bibcode:1989PhT....42g...9A. doi:10.1063/1.2811073.
- ^ Philip W. Anderson (1989). "Spin Glass VI: Spin Glass As Cornucopia" (PDF). Physics Today. 42 (9): 9–11. Bibcode:1989PhT....42i...9A. doi:10.1063/1.2811137.
- ^ Philip W. Anderson (1990). "Spin Glass VII: Spin Glass as Paradigm" (PDF). Physics Today. 43 (3): 9–11. Bibcode:1990PhT....43c...9A. doi:10.1063/1.2810479.
- ^ All of them combined.
- ^ Cannella, V.; Mydosh, J. A. (1972-12-01). "Magnetic Ordering in Gold-Iron Alloys". Physical Review B. 6 (11): 4220–4237. Bibcode:1972PhRvB...6.4220C. doi:10.1103/PhysRevB.6.4220.
- ^ Mulder, C. A. M.; van Duyneveldt, A. J.; Mydosh, J. A. (1981-02-01). "Susceptibility of the $\mathrm{Cu}\mathrm{Mn}$ spin-glass: Frequency and field dependences". Physical Review B. 23 (3): 1384–1396. doi:10.1103/PhysRevB.23.1384.
- ^ Sherrington, David; Kirkpatrick, Scott (1975-12-29). "Solvable Model of a Spin-Glass". Physical Review Letters. 35 (26): 1792–1796. Bibcode:1975PhRvL..35.1792S. doi:10.1103/physrevlett.35.1792. ISSN 0031-9007.
- ^ Parisi, G. (1979-12-03). "Infinite Number of Order Parameters for Spin-Glasses". Physical Review Letters. 43 (23): 1754–1756. Bibcode:1979PhRvL..43.1754P. doi:10.1103/PhysRevLett.43.1754. ISSN 0031-9007.
- ^ Gardner, E; Deridda, B (7 January 1988). "Optimal storage properties of neural network models" (PDF). J. Phys. A. 21 (1): 271. Bibcode:1988JPhA...21..271G. doi:10.1088/0305-4470/21/1/031.
Literature
editExpositions
edit- Stein, Daniel L.; Newman, Charles M. (2013). Spin glasses and complexity. Primers in complex systems. Princeton: Princeton University Press. ISBN 978-0-691-14733-8. Popular exposition, with a minimal amount of mathematics.
- Montanari, Andrea; Sen, Subhabrata (2024-01-09). "A Friendly Tutorial on Mean-Field Spin Glass Techniques for Non-Physicists". Foundations and Trends in Machine Learning. 17 (1): 1–173. arXiv:2204.02909. doi:10.1561/2200000105. ISSN 1935-8237. A practical tutorial introduction.
- Mézard, Marc; Montanari, Andrea (2009). Information, Physics, and Computation. Oxford, U.K.: Oxford University Press. ISBN 9780198570837. OCLC 234430714. 1st 15 chapters of 2008 draft version, available at www.stat.ucla.edu Textbook that focuses on the cavity method and the applications to computer science, especially constraint satisfaction problems.
- Nishimori, Hidetoshi (2001). Statistical physics of spin glasses and information processing: an introduction. International series of monographs on physics. Oxford; New York: Oxford University Press. ISBN 978-0-19-850940-0. OCLC 47063323. Introduction focused on computer science applications, including neural networks.
- Mydosh, J. A. (1993). Spin glasses: an experimental introduction. London; Washington, DC: Taylor & Francis. ISBN 978-0-7484-0038-6. Focuses on the experimentally measurable properties of spin glasses (such as copper-manganese alloy).
- Fischer, K. H.; Hertz, John (1991). Spin glasses. Cambridge studies in magnetism. Cambridge; New York, NY, USA: Cambridge University Press. ISBN 978-0-521-34296-4. Covers mean field theory, experimental data, and numerical simulations.
- Mezard, Marc; Parisi, Giorgio; Virasoro, Miguel Angel (1987), Spin glass theory and beyond, Singapore: World Scientific, ISBN 978-9971-5-0115-0. Early exposition containing the pre-1990 breakthroughs, such as the replica trick.
- De Dominicis, Cirano; Giardina, Irene (2006). Random fields and spin glasses: a field theory approach. Cambridge, UK; New York: Cambridge University Press. ISBN 978-0-521-84783-4. OCLC 70764844. Approach via statistical field theory.
- Talagrand, Michel (2010). Mean field models for spin glasses. 1: Basic examples. Ergebnisse der Mathematik und ihrer Grenzgebiete (Softcover repr. of the harcover 1st ed. 2010 ed.). Berlin Heidelberg: Springer. ISBN 978-3-642-26598-3. and Talagrand, Michel (2011). Mean field models for spin glasses. Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge = A series of modern surveys in mathematics. Heidelberg; New York: Springer. ISBN 978-3-642-15201-6. OCLC 733249730.. Compendium of rigorously provable results.
Primary sources
edit- Edwards, S.F.; Anderson, P.W. (1975), "Theory of spin glasses", Journal of Physics F: Metal Physics, 5 (5): 965–974, Bibcode:1975JPhF....5..965E, doi:10.1088/0305-4608/5/5/017. ShieldSquare Captcha
- Sherrington, David; Kirkpatrick, Scott (1975), "Solvable model of a spin-glass", Physical Review Letters, 35 (26): 1792–1796, Bibcode:1975PhRvL..35.1792S, doi:10.1103/PhysRevLett.35.1792. Papercore Summary http://papercore.org/Sherrington1975
- Nordblad, P.; Lundgren, L.; Sandlund, L. (1986), "A link between the relaxation of the zero field cooled and the thermoremanent magnetizations in spin glasses", Journal of Magnetism and Magnetic Materials, 54: 185–186, Bibcode:1986JMMM...54..185N, doi:10.1016/0304-8853(86)90543-3.
- Binder, K.; Young, A. P. (1986), "Spin glasses: Experimental facts, theoretical concepts, and open questions", Reviews of Modern Physics, 58 (4): 801–976, Bibcode:1986RvMP...58..801B, doi:10.1103/RevModPhys.58.801.
- Bryngelson, Joseph D.; Wolynes, Peter G. (1987), "Spin glasses and the statistical mechanics of protein folding", Proceedings of the National Academy of Sciences, 84 (21): 7524–7528, Bibcode:1987PNAS...84.7524B, doi:10.1073/pnas.84.21.7524, PMC 299331, PMID 3478708....
- Parisi, G. (1980), "The order parameter for spin glasses: a function on the interval 0-1" (PDF), J. Phys. A: Math. Gen., 13 (3): 1101–1112, Bibcode:1980JPhA...13.1101P, doi:10.1088/0305-4470/13/3/042 Papercore Summary http://papercore.org/Parisi1980.
- Talagrand, Michel (2000), "Replica symmetry breaking and exponential inequalities for the Sherrington–Kirkpatrick model", Annals of Probability, 28 (3): 1018–1062, doi:10.1214/aop/1019160325, JSTOR 2652978.
- Guerra, F.; Toninelli, F. L. (2002), "The thermodynamic limit in mean field spin glass models", Communications in Mathematical Physics, 230 (1): 71–79, arXiv:cond-mat/0204280, Bibcode:2002CMaPh.230...71G, doi:10.1007/s00220-002-0699-y, S2CID 16833848
External links
edit- Statistics of frequency of the term "Spin glass" in arxiv.org


