
Summary
3-3 duoprism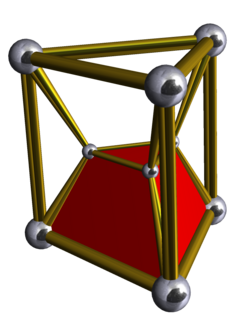 Schlegel diagram | |
|---|---|
| Type | Uniform duoprism |
| Schläfli symbol | {3}×{3} = {3}2 |
| Coxeter diagram | |
| Cells | 6 triangular prisms |
| Faces | 9 squares, 6 triangles |
| Edges | 18 |
| Vertices | 9 |
| Vertex figure | 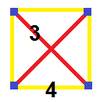 Tetragonal disphenoid |
| Symmetry | [[3,2,3]] = [6,2+,6], order 72 |
| Dual | 3-3 duopyramid |
| Properties | convex, vertex-uniform, facet-transitive |
In the geometry of 4 dimensions, the 3-3 duoprism or triangular duoprism is a four-dimensional convex polytope. It can be constructed as the Cartesian product of two triangles and is the simplest of an infinite family of four-dimensional polytopes constructed as Cartesian products of two polygons, the duoprisms.
It has 9 vertices, 18 edges, 15 faces (9 squares, and 6 triangles), in 6 triangular prism cells. It has Coxeter diagram ![]()
![]()
![]() , and symmetry [[3,2,3]], order 72. Its vertices and edges form a rook's graph.
, and symmetry [[3,2,3]], order 72. Its vertices and edges form a rook's graph.
Hypervolume edit
The hypervolume of a uniform 3-3 duoprism, with edge length a, is . This is the square of the area of an equilateral triangle, .
Graph edit
The graph of vertices and edges of the 3-3 duoprism has 9 vertices and 18 edges. Like the Berlekamp–van Lint–Seidel graph and the unknown solution to Conway's 99-graph problem, every edge is part of a unique triangle and every non-adjacent pair of vertices is the diagonal of a unique square. It is a toroidal graph, a locally linear graph, a strongly regular graph with parameters (9,4,1,2), the rook's graph, and the Paley graph of order 9.[1] This graph is also the Cayley graph of the group with generating set .
Images edit
| Net | 3D perspective projection with 2 different rotations |
|---|
Symmetry edit
In 5-dimensions, some uniform 5-polytopes have 3-3 duoprism vertex figures, some with unequal edge-lengths and therefore lower symmetry:
| Symmetry | [[3,2,3]], order 72 | [3,2], order 12 | ||
|---|---|---|---|---|
| Coxeter diagram |
|
|||
| Schlegel diagram |
||||
| Name | t2α5 | t03α5 | t03γ5 | t03β5 |
The birectified 16-cell honeycomb also has a 3-3 duoprism vertex figure. There are three constructions for the honeycomb with two lower symmetries.
| Symmetry | [3,2,3], order 36 | [3,2], order 12 | [3], order 6 |
|---|---|---|---|
| Coxeter diagram |
|||
| Skew orthogonal projection |
Related complex polygons edit
The regular complex polytope 3{4}2, , in has a real representation as a 3-3 duoprism in 4-dimensional space. 3{4}2 has 9 vertices, and 6 3-edges. Its symmetry is 3[4]2, order 18. It also has a lower symmetry construction, , or 3{}×3{}, with symmetry 3[2]3, order 9. This is the symmetry if the red and blue 3-edges are considered distinct.[2]
| Perspective projection |
Orthogonal projection with coinciding central vertices |
Orthogonal projection, offset view to avoid overlapping elements. |
Related polytopes edit
| Space | Finite | Euclidean | Hyperbolic | ||
|---|---|---|---|---|---|
| n | 4 | 5 | 6 | 7 | 8 |
| Coxeter group |
A2A2 | E6 | =E6+ | =E6++ | |
| Coxeter diagram |
|||||
| Symmetry | [[32,2,-1]] | [[32,2,0]] | [[32,2,1]] | [[32,2,2]] | [[32,2,3]] |
| Order | 72 | 1440 | 103,680 | ∞ | |
| Graph | ∞ | ∞ | |||
| Name | −122 | 022 | 122 | 222 | 322 |
3-3 duopyramid edit
| 3-3 duopyramid | |
|---|---|
| Type | Uniform dual duopyramid |
| Schläfli symbol | {3}+{3} = 2{3} |
| Coxeter diagram | |
| Cells | 9 tetragonal disphenoids |
| Faces | 18 isosceles triangles |
| Edges | 15 (9+6) |
| Vertices | 6 (3+3) |
| Symmetry | [[3,2,3]] = [6,2+,6], order 72 |
| Dual | 3-3 duoprism |
| Properties | convex, vertex-uniform, facet-transitive |
The dual of a 3-3 duoprism is called a 3-3 duopyramid or triangular duopyramid. It has 9 tetragonal disphenoid cells, 18 triangular faces, 15 edges, and 6 vertices.
It can be seen in orthogonal projection as a 6-gon circle of vertices, and edges connecting all pairs, just like a 5-simplex seen in projection.
Related complex polygon edit
The regular complex polygon 2{4}3, also 3{ }+3{ } has 6 vertices in with a real representation in matching the same vertex arrangement of the 3-3 duopyramid. It has 9 2-edges corresponding to the connecting edges of the 3-3 duopyramid, while the 6 edges connecting the two triangles are not included. It can be seen in a hexagonal projection with 3 sets of colored edges. This arrangement of vertices and edges makes a complete bipartite graph with each vertex from one triangle is connected to every vertex on the other. It is also called a Thomsen graph or 4-cage.[3]
| The 2{4}3 with 6 vertices in blue and red connected by 9 2-edges as a complete bipartite graph. |
It has 3 sets of 3 edges, seen here with colors. |
See also edit
- 3-4 duoprism
- Tesseract (4-4 duoprism)
- 5-5 duoprism
- Convex regular 4-polytope
- Duocylinder
Notes edit
- ^ Makhnev, A. A.; Minakova, I. M. (January 2004), "On automorphisms of strongly regular graphs with parameters , ", Discrete Mathematics and Applications, 14 (2), doi:10.1515/156939204872374, MR 2069991, S2CID 118034273
- ^ Coxeter, H. S. M.; Regular Complex Polytopes, Cambridge University Press, (1974).
- ^ Regular Complex Polytopes, p.110, p.114
References edit
- Regular Polytopes, H. S. M. Coxeter, Dover Publications, Inc., 1973, New York, p. 124.
- Coxeter, The Beauty of Geometry: Twelve Essays, Dover Publications, 1999, ISBN 0-486-40919-8 (Chapter 5: Regular Skew Polyhedra in three and four dimensions and their topological analogues)
- Coxeter, H. S. M. Regular Skew Polyhedra in Three and Four Dimensions. Proc. London Math. Soc. 43, 33-62, 1937.
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26)
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- Catalogue of Convex Polychora, section 6, George Olshevsky.
- Apollonian Ball Packings and Stacked Polytopes Discrete & Computational Geometry, June 2016, Volume 55, Issue 4, pp 801–826
External links edit
- The Fourth Dimension Simply Explained—describes duoprisms as "double prisms" and duocylinders as "double cylinders"
- Polygloss – glossary of higher-dimensional terms
- Exploring Hyperspace with the Geometric Product



