
Summary
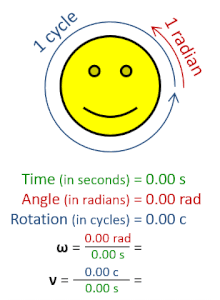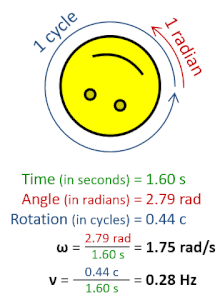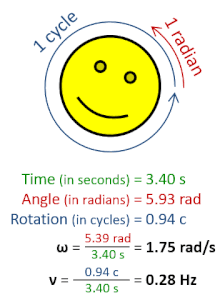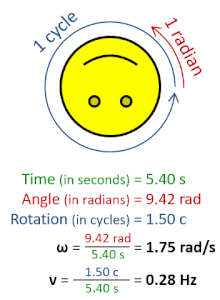
In physics, angular frequency (symbol ω), also called angular speed and angular rate, is a scalar measure of the angle rate (the angle per unit time) or the temporal rate of change of the phase argument of a sinusoidal waveform or sine function (for example, in oscillations and waves). Angular frequency (or angular speed) is the magnitude of the pseudovector quantity angular velocity.[1]
| Angular frequency | |
|---|---|
 | |
Other names | angular speed, angular rate |
Common symbols | ω |
| SI unit | radian per second (rad/s) |
Other units | degrees per second (°/s) |
| In SI base units | s−1 |
Derivations from other quantities | ω=2π rad ⋅ ν, ω=dθ/dt |
| Dimension | |

Angular frequency can be obtained multiplying rotational frequency, ν (or ordinary frequency, f) by a full turn (2π radians): ω = 2π rad⋅ν. It can also be formulated as ω = dθ/dt, the instantaneous rate of change of the angular displacement, θ, with respect to time, t.[2][3]
Unit
editIn SI units, angular frequency is normally presented in the unit radian per second. The unit hertz (Hz) is dimensionally equivalent, but by convention it is only used for frequency f, never for angular frequency ω. This convention is used to help avoid the confusion[4] that arises when dealing with quantities such as frequency and angular quantities because the units of measure (such as cycle or radian) are considered to be one and hence may be omitted when expressing quantities in terms of SI units.[5][6]
In digital signal processing, the frequency may be normalized by the sampling rate, yielding the normalized frequency.
Examples
editCircular motion
editIn a rotating or orbiting object, there is a relation between distance from the axis, , tangential speed, , and the angular frequency of the rotation. During one period, , a body in circular motion travels a distance . This distance is also equal to the circumference of the path traced out by the body, . Setting these two quantities equal, and recalling the link between period and angular frequency we obtain: Circular motion on the unit circle is given by where:
- ω is the angular frequency (SI unit: radians per second),
- T is the period (SI unit: seconds),
- f is the ordinary frequency (SI unit: hertz).
Oscillations of a spring
editAn object attached to a spring can oscillate. If the spring is assumed to be ideal and massless with no damping, then the motion is simple and harmonic with an angular frequency given by[7] where
- k is the spring constant,
- m is the mass of the object.
ω is referred to as the natural angular frequency (sometimes be denoted as ω0).
As the object oscillates, its acceleration can be calculated by where x is displacement from an equilibrium position.
Using standard frequency f, this equation would be
LC circuits
editThe resonant angular frequency in a series LC circuit equals the square root of the reciprocal of the product of the capacitance (C, with SI unit farad) and the inductance of the circuit (L, with SI unit henry):[8]
Adding series resistance (for example, due to the resistance of the wire in a coil) does not change the resonant frequency of the series LC circuit. For a parallel tuned circuit, the above equation is often a useful approximation, but the resonant frequency does depend on the losses of parallel elements.
Terminology
editAlthough angular frequency is often loosely referred to as frequency, it differs from frequency by a factor of 2π, which potentially leads confusion when the distinction is not made clear.
See also
editReferences and notes
edit- ^ Cummings, Karen; Halliday, David (2007). Understanding physics. New Delhi: John Wiley & Sons, authorized reprint to Wiley – India. pp. 449, 484, 485, 487. ISBN 978-81-265-0882-2.(UP1)
- ^ "ISO 80000-3:2019 Quantities and units — Part 3: Space and time" (2 ed.). International Organization for Standardization. 2019. Retrieved 2019-10-23. [1] (11 pages)
- ^
Holzner, Steven (2006). Physics for Dummies. Hoboken, New Jersey: Wiley Publishing. pp. 201. ISBN 978-0-7645-5433-9.
angular frequency.
- ^ Lerner, Lawrence S. (1996-01-01). Physics for scientists and engineers. p. 145. ISBN 978-0-86720-479-7.
- ^ Mohr, J. C.; Phillips, W. D. (2015). "Dimensionless Units in the SI". Metrologia. 52 (1): 40–47. arXiv:1409.2794. Bibcode:2015Metro..52...40M. doi:10.1088/0026-1394/52/1/40. S2CID 3328342.
- ^ "SI units need reform to avoid confusion". Editorial. Nature. 548 (7666): 135. 7 August 2011. doi:10.1038/548135b. PMID 28796224.
- ^ Serway, Raymond A.; Jewett, John W. (2006). Principles of physics (4th ed.). Belmont, CA: Brooks / Cole – Thomson Learning. pp. 375, 376, 385, 397. ISBN 978-0-534-46479-0.
- ^ Nahvi, Mahmood; Edminister, Joseph (2003). Schaum's outline of theory and problems of electric circuits. McGraw-Hill Companies (McGraw-Hill Professional). pp. 214, 216. ISBN 0-07-139307-2. (LC1)
Related Reading:
- Olenick, Richard P.; Apostol, Tom M.; Goodstein, David L. (2007). The Mechanical Universe. New York City: Cambridge University Press. pp. 383–385, 391–395. ISBN 978-0-521-71592-8.



