
Summary
The second (symbol: s) is a unit of time, historically defined as 1⁄86400 of a day – this factor derived from the division of the day first into 24 hours, then to 60 minutes and finally to 60 seconds each (24 × 60 × 60 = 86400).
| second | |
|---|---|
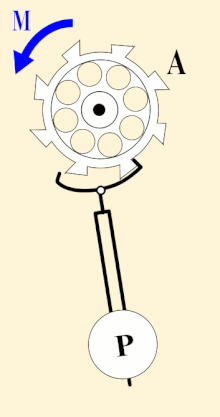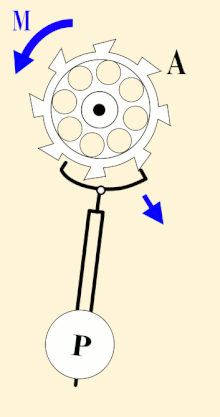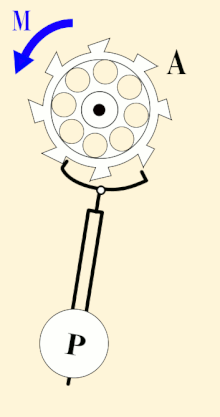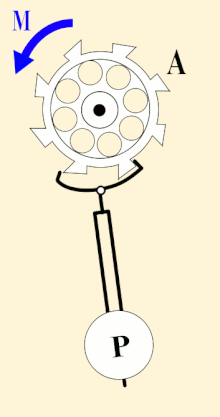 A pendulum-governed escapement of a clock, ticking every second | |
| General information | |
| Unit system | SI |
| Unit of | time |
| Symbol | s |
The current and formal definition in the International System of Units (SI) is more precise:
The second [...] is defined by taking the fixed numerical value of the caesium frequency, ΔνCs, the unperturbed ground-state hyperfine transition frequency of the caesium 133 atom, to be 9192631770 when expressed in the unit Hz, which is equal to s−1.[1]
This current definition was adopted in 1967 when it became feasible to define the second based on fundamental properties of nature with caesium clocks.[2] Because the speed of Earth's rotation varies and is slowing ever so slightly, a leap second is added at irregular intervals to civil time[nb 1] to keep clocks in sync with Earth's rotation.
Etymology
edit"Minute" comes from the Latin pars minuta prima, meaning "first small part" i.e. first division of the hour - dividing into sixty, and "second" comes from the pars minuta secunda, "second small part", dividing again into sixty.[3]
Uses
editAnalog clocks and watches often have sixty tick marks on their faces, representing seconds (and minutes), and a "second hand" to mark the passage of time in seconds. Digital clocks and watches often have a two-digit seconds counter.
SI prefixes are frequently combined with the word second to denote subdivisions of the second: milliseconds (thousandths), microseconds (millionths), nanoseconds (billionths), and sometimes smaller units of a second. Multiples of seconds are usually counted in hours and minutes. Though SI prefixes may also be used to form multiples of the second such as kiloseconds (thousands of seconds), such units are rarely used in practice. An everyday experience with small fractions of a second is a 1-gigahertz microprocessor that has a cycle time of 1 nanosecond. Camera shutter speeds are often expressed in fractions of a second, such as 1⁄30 second or 1⁄1000 second.
Sexagesimal divisions of the day from a calendar based on astronomical observation have existed since the third millennium BC, though they were not seconds as we know them today.[4] Small divisions of time could not be measured back then, so such divisions were mathematically derived. The first timekeepers that could count seconds accurately were pendulum clocks invented in the 17th century. Starting in the 1950s, atomic clocks became better timekeepers than Earth's rotation, and they continue to set the standard today.
Clocks and solar time
editA mechanical clock, which does not depend on measuring the relative rotational position of the Earth, keeps uniform time called mean time, within whatever accuracy is intrinsic to it. That means that every second, minute and every other division of time counted by the clock has the same duration as any other identical division of time. But a sundial, which measures the relative position of the Sun in the sky called apparent time, does not keep uniform time. The time kept by a sundial varies by time of year, meaning that seconds, minutes and every other division of time is a different duration at different times of the year. The time of day measured with mean time versus apparent time may differ by as much as 15 minutes, but a single day differs from the next by only a small amount; 15 minutes is a cumulative difference over a part of the year. The effect is due chiefly to the obliqueness of Earth's axis with respect to its orbit around the Sun.
The difference between apparent solar time and mean time was recognized by astronomers since antiquity, but prior to the invention of accurate mechanical clocks in the mid-17th century, sundials were the only reliable timepieces, and apparent solar time was the only generally accepted standard.
Events and units of time in seconds
editFractions of a second are usually denoted in decimal notation, for example 2.01 seconds, or two and one hundredth seconds. Multiples of seconds are usually expressed as minutes and seconds, or hours, minutes and seconds of clock time, separated by colons, such as 11:23:24, or 45:23 (the latter notation can give rise to ambiguity, because the same notation is used to denote hours and minutes). It rarely makes sense to express longer periods of time like hours or days in seconds, because they are awkwardly large numbers. For the metric unit of second, there are decimal prefixes representing 10−30 to 1030 seconds.
Some common units of time in seconds are: a minute is 60 seconds; an hour is 3,600 seconds; a day is 86,400 seconds; a week is 604,800 seconds; a year (other than leap years) is 31,536,000 seconds; and a (Gregorian) century averages 3,155,695,200 seconds; with all of the above excluding any possible leap seconds. In astronomy, a Julian year is precisely 31,557,600 seconds.
Some common events in seconds are: a stone falls about 4.9 meters from rest in one second; a pendulum of length about one meter has a swing of one second, so pendulum clocks have pendulums about a meter long; the fastest human sprinters run 10 meters in a second; an ocean wave in deep water travels about 23 meters in one second; sound travels about 343 meters in one second in air; light takes 1.3 seconds to reach Earth from the surface of the Moon, a distance of 384,400 kilometers.
Other units incorporating seconds
editA second is directly part of other units, such as frequency measured in hertz (inverse seconds or s−1), speed in meters per second, and acceleration in meters per second squared. The metric system unit becquerel, a measure of radioactive decay, is measured in inverse seconds and higher powers of second are involved in derivatives of acceleration such as jerk. Though many derivative units for everyday things are reported in terms of larger units of time, not seconds, they are ultimately defined in terms of the SI second; this includes time expressed in hours and minutes, velocity of a car in kilometers per hour or miles per hour, kilowatt hours of electricity usage, and speed of a turntable in rotations per minute.
Moreover, most other SI base units are defined by their relationship to the second: the meter is defined by setting the speed of light (in vacuum) to be 299 792 458 m/s, exactly; definitions of the SI base units kilogram, ampere, kelvin, and candela also depend on the second. The only base unit whose definition does not depend on the second is the mole, and only two of the 22 named derived units, radian and steradian, do not depend on the second either.
Timekeeping standards
editA set of atomic clocks throughout the world keeps time by consensus: the clocks "vote" on the correct time, and all voting clocks are steered to agree with the consensus, which is called International Atomic Time (TAI). TAI "ticks" atomic seconds.[5]: 207–218
Civil time is defined to agree with the rotation of the Earth. The international standard for timekeeping is Coordinated Universal Time (UTC). This time scale "ticks" the same atomic seconds as TAI, but inserts or omits leap seconds as necessary to correct for variations in the rate of rotation of the Earth.[5]: 16–17, 207
A time scale in which the seconds are not exactly equal to atomic seconds is UT1, a form of universal time. UT1 is defined by the rotation of the Earth with respect to the Sun, and does not contain any leap seconds.[5]: 68, 232 UT1 always differs from UTC by less than a second.
Optical lattice clock
editWhile they are not yet part of any timekeeping standard, optical lattice clocks with frequencies in the visible light spectrum now exist and are the most accurate timekeepers of all. A strontium clock with frequency 430 THz, in the red range of visible light, during the 2010s held the accuracy record: it gains or loses less than a second in 15 billion years, which is longer than the estimated age of the universe. Such a clock can measure a change in its elevation of as little as 2 cm by the change in its rate due to gravitational time dilation.[6]
History of definition
editThere have only ever been three definitions of the second: as a fraction of the day, as a fraction of an extrapolated year, and as the microwave frequency of a caesium atomic clock, which have each realized a sexagesimal division of the day from ancient astronomical calendars.
Sexagesimal divisions of calendar time and day
editCivilizations in the classic period and earlier created divisions of the calendar as well as arcs using a sexagesimal system of counting, so at that time the second was a sexagesimal subdivision of the day (ancient second = day/60×60), not of the hour like the modern second (= hour/60×60). Sundials and water clocks were among the earliest timekeeping devices, and units of time were measured in degrees of arc. Conceptual units of time smaller than realisable on sundials were also used.
There are references to "second" as part of a lunar month in the writings of natural philosophers of the Middle Ages, which were mathematical subdivisions that could not be measured mechanically.[nb 2][nb 3]
Fraction of solar day
editThe earliest mechanical clocks, which appeared starting in the 14th century, had displays that divided the hour into halves, thirds, quarters and sometimes even 12 parts, but never by 60. In fact, the hour was not commonly divided in 60 minutes as it was not uniform in duration. It was not practical for timekeepers to consider minutes until the first mechanical clocks that displayed minutes appeared near the end of the 16th century. Mechanical clocks kept the mean time, as opposed to the apparent time displayed by sundials. By that time, sexagesimal divisions of time were well established in Europe.[nb 4]
The earliest clocks to display seconds appeared during the last half of the 16th century. The second became accurately measurable with the development of mechanical clocks. The earliest spring-driven timepiece with a second hand that marked seconds is an unsigned clock depicting Orpheus in the Fremersdorf collection, dated between 1560 and 1570.[9]: 417–418 [10] During the 3rd quarter of the 16th century, Taqi al-Din built a clock with marks every 1/5 minute.[11] In 1579, Jost Bürgi built a clock for William of Hesse that marked seconds.[9]: 105 In 1581, Tycho Brahe redesigned clocks that had displayed only minutes at his observatory so they also displayed seconds, even though those seconds were not accurate. In 1587, Tycho complained that his four clocks disagreed by plus or minus four seconds.[9]: 104
In 1656, Dutch scientist Christiaan Huygens invented the first pendulum clock. It had a pendulum length of just under a meter, giving it a swing of one second, and an escapement that ticked every second. It was the first clock that could accurately keep time in seconds. By the 1730s, 80 years later, John Harrison's maritime chronometers could keep time accurate to within one second in 100 days.
In 1832, Gauss proposed using the second as the base unit of time in his millimeter–milligram–second system of units. The British Association for the Advancement of Science (BAAS) in 1862 stated that "All men of science are agreed to use the second of mean solar time as the unit of time."[12] BAAS formally proposed the CGS system in 1874, although this system was gradually replaced over the next 70 years by MKS units. Both the CGS and MKS systems used the same second as their base unit of time. MKS was adopted internationally during the 1940s, defining the second as 1⁄86,400 of a mean solar day.
Fraction of an ephemeris year
editSometime in the late 1940s, quartz crystal oscillator clocks with an operating frequency of ~100 kHz advanced to keep time with accuracy better than 1 part in 108 over an operating period of a day. It became apparent that a consensus of such clocks kept better time than the rotation of the Earth. Metrologists also knew that Earth's orbit around the Sun (a year) was much more stable than Earth's rotation. This led to proposals as early as 1950 to define the second as a fraction of a year.
The Earth's motion was described in Newcomb's Tables of the Sun (1895), which provided a formula for estimating the motion of the Sun relative to the epoch 1900 based on astronomical observations made between 1750 and 1892.[13] This resulted in adoption of an ephemeris time scale expressed in units of the sidereal year at that epoch by the IAU in 1952.[14] This extrapolated timescale brings the observed positions of the celestial bodies into accord with Newtonian dynamical theories of their motion.[13] In 1955, the tropical year, considered more fundamental than the sidereal year, was chosen by the IAU as the unit of time. The tropical year in the definition was not measured but calculated from a formula describing a mean tropical year that decreased linearly over time.
In 1956, the second was redefined in terms of a year relative to that epoch. The second was thus defined as "the fraction 1⁄31,556,925.9747 of the tropical year for 1900 January 0 at 12 hours ephemeris time".[13] This definition was adopted as part of the International System of Units in 1960.[15]
Atomic definition
editEven the best mechanical, electric motorized and quartz crystal-based clocks develop discrepancies from environmental conditions; far better for timekeeping is the natural and exact "vibration" in an energized atom. The frequency of vibration (i.e., radiation) is very specific depending on the type of atom and how it is excited.[16] Since 1967, the second has been defined as exactly "the duration of 9,192,631,770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the caesium-133 atom". This length of a second was selected to correspond exactly to the length of the ephemeris second previously defined. Atomic clocks use such a frequency to measure seconds by counting cycles per second at that frequency. Radiation of this kind is one of the most stable and reproducible phenomena of nature. The current generation of atomic clocks is accurate to within one second in a few hundred million years. Since 1967, atomic clocks based on atoms other than caesium-133 have been developed with increased precision by a factor of 100. Therefore a new definition of the second is planned.[17]
Atomic clocks now set the length of a second and the time standard for the world.[5]: 231–232
Table
edit| Evolution of the Second | ||
|---|---|---|
| Decisions of the CIPM | Resolution of the CGPM | Information |
| That according to the decisions of the 8th General Assembly of the International Astronomical Union (Rome, 1952), the second of ephemeris time (ET) is the fraction
of the tropical year for 1900 January 0 at 12 h ET. |
The second is the fraction of the tropical year for 1900 January 0 at 12 hours ephemeris time. | 1956 CIPM
11th CGPM 1960 Resolution 9 |
| The standard to be employed is the transition between the hyperfine levels F=4, M=0 and F=3, M=0 of the ground state of the caesium 133 atom, unperturbed by external fields, and that the frequency of this transition is assigned the value 9192631770 hertz. | The second is the duration of 9 192 631 770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the caesium 133 atom | 13th CGPM Resolution 1
CIPM 1967 |
| This definition implies that the caesium atom is at rest and unperturbed. In consequence, in its practical realization, measurements must be corrected for velocity of the atoms with respect to the clock reference frame, for magnetic and electric fields including ambient black-body radiation, for spin-exchange effects and for other possible perturbations. | At its 1997 meeting, the CIPM affirmed that: This definition refers to a caesium atom at rest at a temperature of 0 K. This note was intended to make it clear that the definition of the SI second is based on a Cs atom unperturbed by black-body radiation, that is, in an environment whose temperature is 0 K, and that the frequencies of primary frequency standards should therefore be corrected for the shift due to ambient radiation, as stated at the meeting of the CCTF in 1999. | footnote added by the 14th meeting of the Consultative Committee for Time and Frequency in 1999
the footnote was added at the 86th (1997) meeting of the CIPM GCPM 1998 7th Edition SI Brochure |
| The definition of a unit refers to an idealized situation that can be reached in the practical realization with some uncertainty only. In this spirit, the definition of the second has to be understood as referring to atoms free of any perturbation, at rest and in the absence of electric and magnetic fields.
A future re-definition of the second would be justified if these idealized conditions can be achieved much easier than with the current definition. The definition of the second should be understood as the definition of the unit of proper time: it applies in a small spatial domain that shares the motion of the caesium atom used to realize the definition. In a laboratory sufficiently small to allow the effects of the non-uniformity of the gravitational field to be neglected when compared to the uncertainties of the realization of the second, the proper second is obtained after application of the special relativistic correction for the velocity of the atom in the laboratory. It is wrong to correct for the local gravitational field. |
The second, symbol s, is the SI unit of time. It is defined by taking the fixed numerical value of the caesium frequency, ΔνCs, the unperturbed ground-state hyperfine transition frequency of the caesium 133 atom, to be 9 192 631 770 when expressed in the unit Hz, which is equal to s−1.
The reference to an unperturbed atom is intended to make it clear that the definition of the SI second is based on an isolated caesium atom that is unperturbed by any external field, such as ambient black-body radiation. The second, so defined, is the unit of proper time in the sense of the general theory of relativity. To allow the provision of a coordinated time scale, the signals of different primary clocks in different locations are combined, which have to be corrected for relativistic caesium frequency shifts (see section 2.3.6). The CIPM has adopted various secondary representations of the second, based on a selected number of spectral lines of atoms, ions or molecules. The unperturbed frequencies of these lines can be determined with a relative uncertainty not lower than that of the realization of the second based on the 133Cs hyperfine transition frequency, but some can be reproduced with superior stability. |
Current Definition resolved in 2018 effective after the 26th GCPM approved the redefinition May 20, 2019.
SI Brochure 9 |
Future redefinition
editIn 2022, the best realisation of the second is done with caesium primary standard clocks such as IT-CsF2, NIST-F2, NPL-CsF2, PTB-CSF2, SU–CsFO2 or SYRTE-FO2. These clocks work by laser-cooling a cloud of Cs atoms to a microkelvin in a magneto-optic trap. These cold atoms are then launched vertically by laser light. The atoms then undergo Ramsey excitation in a microwave cavity. The fraction of excited atoms is then detected by laser beams. These clocks have 5×10−16 systematic uncertainty, which is equivalent to 50 picoseconds per day. A system of several fountains worldwide contribute to International Atomic Time. These caesium clocks also underpin optical frequency measurements.
Optical clocks are based on forbidden optical transitions in ions or atoms. They have frequencies around 1015 Hz, with a natural linewidth of typically 1 Hz, so the Q-factor is about 1015, or even higher. They have better stabilities than microwave clocks, which means that they can facilitate evaluation of lower uncertainties. They also have better time resolution, which means the clock "ticks" faster.[18] Optical clocks use either a single ion, or an optical lattice with 104–106 atoms.
Rydberg constant
editA definition based on the Rydberg constant would involve fixing the value to a certain value: . The Rydberg constant describes the energy levels in a hydrogen atom with the nonrelativistic approximation .
The only viable way to fix the Rydberg constant involves trapping and cooling hydrogen. This is difficult because it is very light and the atoms move very fast, causing Doppler shifts. The radiation needed to cool the hydrogen – 121.5 nm – is also difficult. Another hurdle involves improving the uncertainty in QED calculations, specifically the Lamb shift in the 1s-2s transition of the hydrogen atom.[19]
Requirements
editA redefinition must include improved optical clock reliability. TAI must be contributed to by optical clocks before the BIPM affirms a redefinition. A consistent method of sending signals must be developed before the second is redefined, such as fiber-optics.[19]
SI multiples
editSI prefixes are commonly used for times shorter than one second, but rarely for multiples of a second. Instead, certain non-SI units are permitted for use with SI: minutes, hours, days, and in astronomy Julian years.[20]
| Submultiples | Multiples | ||||||
|---|---|---|---|---|---|---|---|
| Value | SI symbol | Name | Value | SI symbol | Name | Equivalent to | |
| 10−1 s | ds | decisecond | 101 s | das | decasecond | 10 seconds | |
| 10−2 s | cs | centisecond | 102 s | hs | hectosecond | 1 minute, 40 seconds | |
| 10−3 s | ms | millisecond | 103 s | ks | kilosecond | 16 minutes, 40 seconds | |
| 10−6 s | μs | microsecond | 106 s | Ms | megasecond | 11 days, 13 hours, 46 minutes, 40 seconds | |
| 10−9 s | ns | nanosecond | 109 s | Gs | gigasecond | 31.7 years | |
| 10−12 s | ps | picosecond | 1012 s | Ts | terasecond | 31,700 years | |
| 10−15 s | fs | femtosecond | 1015 s | Ps | petasecond | 31.7 million years | |
| 10−18 s | as | attosecond | 1018 s | Es | exasecond | 31.7 billion years | |
| 10−21 s | zs | zeptosecond | 1021 s | Zs | zettasecond | 31.7 trillion years | |
| 10−24 s | ys | yoctosecond | 1024 s | Ys | yottasecond | 31.7 quadrillion years | |
| 10−27 s | rs | rontosecond | 1027 s | Rs | ronnasecond | 31.7 quintillion years | |
| 10−30 s | qs | quectosecond | 1030 s | Qs | quettasecond | 31.7 sextillion years | |
See also
editNotes
edit- ^ Civil time is set, directly or indirectly, to Coordinated Universal Time, which includes leap seconds. Other time scales are used in scientific and technical fields that do not contain leap seconds.
- ^ In 1000, the Persian scholar al-Biruni, writing in Arabic, used the term second, and defined the division of time between new moons of certain specific weeks as a number of days, hours, minutes, seconds, thirds, and fourths after noon Sunday.[7]
- ^ In 1267, the medieval English scientist Roger Bacon, writing in Latin, defined the division of time between full moons as a number of hours, minutes, seconds, thirds, and fourths (horae, minuta, secunda, tertia, and quarta) after noon on specified calendar dates.[8]
- ^ It may be noted that 60 is the smallest multiple of the first 6 counting numbers. So a clock with 60 divisions would have a mark for thirds, fourths, fifths, sixths and twelfths (the hours); whatever units the clock would likely keep time in, would have marks.
References
edit- ^ "SI Brochure (2019)" (PDF). SI Brochure. BIPM. p. 130. Archived (PDF) from the original on May 23, 2019. Retrieved May 23, 2019.
- ^ Gill, Patrick (October 28, 2011). "When should we change the definition of the second?". Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences. 369 (1953): 4109–4130. Bibcode:2011RSPTA.369.4109G. doi:10.1098/rsta.2011.0237. PMID 21930568. S2CID 6896025.
- ^ "second | Etymology of second by etymonline". www.etymonline.com. Retrieved October 4, 2024.
- ^ "mathematics – Ancient mathematical sources". Encyclopedia Britannica. Retrieved September 20, 2021.
- ^ a b c d McCarthy, Dennis D.; Seidelmann, P. Kenneth (2009). Time: From Earth Rotation to Atomic Physics. Weinheim: Wiley.
- ^ Vincent, James (April 22, 2015). "The most accurate clock ever built only loses one second every 15 billion years". TheVerge. Archived from the original on January 27, 2018. Retrieved January 26, 2018.
- ^ Al-Biruni (1879) [1000]. The chronology of ancient nations. Translated by Sachau, C. Edward. pp. 147–149. Archived from the original on September 16, 2019. Retrieved February 23, 2016.
- ^ Bacon, Roger (2000) [1267]. The Opus Majus of Roger Bacon. translated by Robert Belle Burke. University of Pennsylvania Press. table facing page 231. ISBN 1-85506-856-7.
- ^ a b c Landes, David S. (1983). Revolution in Time. Cambridge, Massachusetts: Harvard University Press. ISBN 0-674-76802-7.
- ^ Willsberger, Johann (1975). Clocks & watches. New York: Dial Press. ISBN 0-8037-4475-7. full page color photo: 4th caption page, 3rd photo thereafter (neither pages nor photos are numbered).
- ^ Selin, Helaine (July 31, 1997). Encyclopaedia of the History of Science, Technology, and Medicine in Non-Western Cultures. Springer Science & Business Media. p. 934. ISBN 0-7923-4066-3. Archived from the original on November 20, 2016. Retrieved February 23, 2016.
- ^ Jenkin, Henry Charles Fleeming, ed. (1873). Reports of the committee on electrical standards. British Association for the Advancement of Science. p. 90. Archived from the original on November 20, 2016. Retrieved February 23, 2016.
- ^ a b c "Leap Seconds". Time Service Department, United States Naval Observatory. Archived from the original on March 12, 2015. Retrieved November 22, 2015.
- ^
Nautical Almanac Offices of the United Kingdom and the United States of America (1961), Explanatory Supplement to the Astronomical Ephemeris and the American Ephemeris and Nautical Almanac, p. 9,
... defined ephemeris time ... [was] adopted by the International Astronomical Union in Sept. 1952.
- ^ "SI Brochure (2006)" (PDF). SI Brochure 8th Edition. BIPM. p. 112. Archived (PDF) from the original on May 3, 2019. Retrieved May 23, 2019.
- ^ McCarthy, Dennis D.; Seidelmann, P. Kenneth (2009). "Definition and Role of a Second". Time: From Earth Rotation to Atomic Physics. Weinheim: Wiley.
- ^ Draft resolutions of the 27. General Conference on Weights and Measures in November 2022, Section E, p. 25
- ^ National Physical Laboratory (2011). "When should we change the definition of the second?". Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences. 369 (1953): 4109–4130. Bibcode:2011RSPTA.369.4109G. doi:10.1098/rsta.2011.0237. PMID 21930568. S2CID 6896025.
- ^ a b Gill, Patrick (October 28, 2011). "When should we change the definition of the second?". Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences. 369 (1953): 4109–4130. Bibcode:2011RSPTA.369.4109G. doi:10.1098/rsta.2011.0237. PMID 21930568. S2CID 6896025.
- ^ International Astronomical Union. "Recommendations Concerning Units". Archived from the original on February 16, 2007. Retrieved February 18, 2007. Reprinted from the "IAU Style Manual" by G.A. Wilkinson, Comm. 5, in IAU Transactions XXB (1987).
External links
edit- National Physical Laboratory: Trapped ion optical frequency standards
- High-accuracy strontium ion optical clock; National Physical Laboratory (2005)
- National Research Council of Canada: Optical frequency standard based on a single trapped ion
- NIST: Definition of the second; notice the cesium atom must be in its ground state at 0 K
- Official BIPM definition of the second
- The leap second: its history and possible future
- What is a Cesium atom clock?
- SLAC: Scales of Time – Our universe from 1018 to 10−18 seconds


