
Summary
In geometry, an epitrochoid (/ɛpɪˈtrɒkɔɪd/ or /ɛpɪˈtroʊkɔɪd/) is a roulette traced by a point attached to a circle of radius r rolling around the outside of a fixed circle of radius R, where the point is at a distance d from the center of the exterior circle.
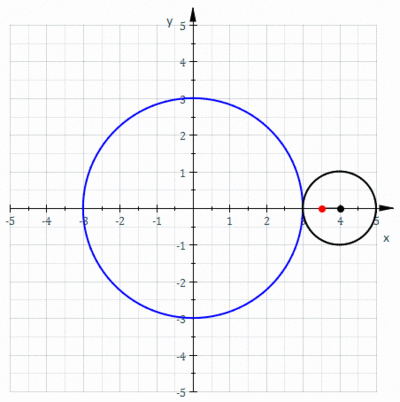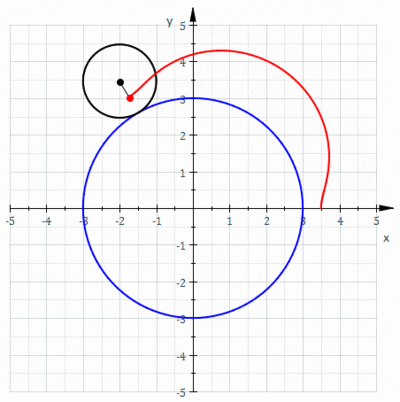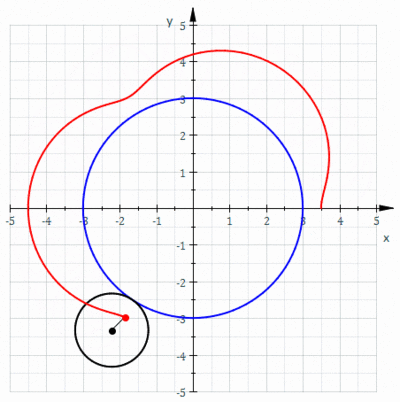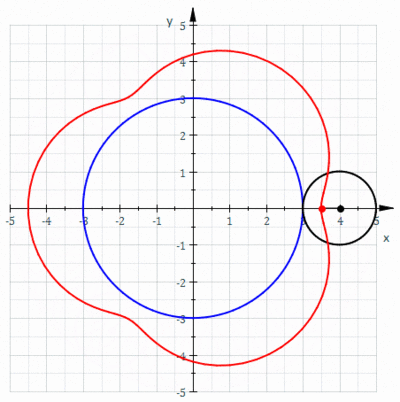
The parametric equations for an epitrochoid are
The parameter θ is geometrically the polar angle of the center of the exterior circle. (However, θ is not the polar angle of the point on the epitrochoid.)
Special cases include the limaçon with R = r and the epicycloid with d = r.
The classic Spirograph toy traces out epitrochoid and hypotrochoid curves.
The paths of planets in the once popular geocentric system of deferents and epicycles are epitrochoids with for both the outer planets and the inner planets.
The orbit of the Moon, when centered around the Sun, approximates an epitrochoid.
The combustion chamber of the Wankel engine is an epitrochoid.
See also edit
References edit
- J. Dennis Lawrence (1972). A catalog of special plane curves. Dover Publications. pp. 160–164. ISBN 0-486-60288-5.
External links edit
- Epitrochoid generator
- Weisstein, Eric W. "Epitrochoid". MathWorld.
- Visual Dictionary of Special Plane Curves on Xah Lee 李杀网
- Interactive simulation of the geocentric graphical representation of planet paths
- O'Connor, John J.; Robertson, Edmund F., "Epitrochoid", MacTutor History of Mathematics Archive, University of St Andrews
- Plot Epitrochoid -- GeoFun





