
Summary
In mathematics, the floor function (or greatest integer function) is the function that takes as input a real number x, and gives as output the greatest integer less than or equal to x, denoted ⌊x⌋ or floor(x). Similarly, the ceiling function maps x to the smallest integer greater than or equal to x, denoted ⌈x⌉ or ceil(x).[1]
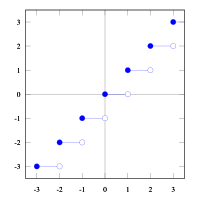

For example, for floor: ⌊2.4⌋ = 2, ⌊−2.4⌋ = −3, and for ceiling: ⌈2.4⌉ = 3, and ⌈−2.4⌉ = −2.
Historically, the floor of x has been–and still is–called the integral part or integer part of x, often denoted [x] (as well as a variety of other notations).[2] However, the same term, integer part, is also used for truncation towards zero, which differs from the floor function for negative numbers.
For n an integer, ⌊n⌋ = ⌈n⌉ = [n] = n.
Although floor(x+1) and ceil(x) produce graphs that appear exactly alike, they are not the same when the value of x is an exact integer. For example, when x=2.0001; ⌊2.0001+1⌋ = ⌈2.0001⌉ = 3. However, if x=2, then ⌊2+1⌋ = 3, while ⌈2⌉ = 2.
| x | Floor ⌊x⌋ | Ceiling ⌈x⌉ | Fractional part {x} |
|---|---|---|---|
| 2 | 2 | 2 | 0 |
| 2.0001 | 2 | 3 | 0.0001 |
| 2.4 | 2 | 3 | 0.4 |
| 2.9 | 2 | 3 | 0.9 |
| 2.999 | 2 | 3 | 0.999 |
| −2.7 | −3 | −2 | 0.3 |
| −2 | −2 | −2 | 0 |
Notation edit
The integral part or integer part of a number (partie entière in the original) was first defined in 1798 by Adrien-Marie Legendre in his proof of the Legendre's formula.
Carl Friedrich Gauss introduced the square bracket notation [x] in his third proof of quadratic reciprocity (1808).[3] This remained the standard[4] in mathematics until Kenneth E. Iverson introduced, in his 1962 book A Programming Language, the names "floor" and "ceiling" and the corresponding notations ⌊x⌋ and ⌈x⌉.[5][6] (Iverson used square brackets for a different purpose, the Iverson bracket notation.) Both notations are now used in mathematics, although Iverson's notation will be followed in this article.
In some sources, boldface or double brackets ⟦x⟧ are used for floor, and reversed brackets ⟧x⟦ or ]x[ for ceiling.[7][8]
The fractional part is the sawtooth function, denoted by {x} for real x and defined by the formula
- {x} = x − ⌊x⌋[9]
For all x,
- 0 ≤ {x} < 1.
These characters are provided in Unicode:
- U+2308 ⌈ LEFT CEILING (⌈, ⌈)
- U+2309 ⌉ RIGHT CEILING (⌉, ⌉)
- U+230A ⌊ LEFT FLOOR (⌊, ⌊)
- U+230B ⌋ RIGHT FLOOR (⌋, ⌋)
In the LaTeX typesetting system, these symbols can be specified with the \lceil, \rceil, \lfloor, and \rfloor commands in math mode, and extended in size using \left\lceil, \right\rceil, \left\lfloor, and \right\rfloor as needed.
Some authors define [x] as the round-toward-zero function[citation needed], so [2.4] = 2 and [−2.4] = −2, and call it the "integer part".
Definition and properties edit
Given real numbers x and y, integers m and n and the set of integers , floor and ceiling may be defined by the equations
Since there is exactly one integer in a half-open interval of length one, for any real number x, there are unique integers m and n satisfying the equation
where and may also be taken as the definition of floor and ceiling.
Equivalences edit
These formulas can be used to simplify expressions involving floors and ceilings.[10]
In the language of order theory, the floor function is a residuated mapping, that is, part of a Galois connection: it is the upper adjoint of the function that embeds the integers into the reals.
These formulas show how adding an integer n to the arguments affects the functions:
The above are never true if n is not an integer; however, for every x and y, the following inequalities hold:
Monotonicity edit
Both floor and ceiling functions are monotonically non-decreasing functions:
Relations among the functions edit
It is clear from the definitions that
- with equality if and only if x is an integer, i.e.
In fact, for integers n, both floor and ceiling functions are the identity:
Negating the argument switches floor and ceiling and changes the sign:
and:
Negating the argument complements the fractional part:
The floor, ceiling, and fractional part functions are idempotent:
The result of nested floor or ceiling functions is the innermost function:
due to the identity property for integers.
Quotients edit
If m and n are integers and n ≠ 0,
If n is a positive integer[11]
If m is positive[12]
For m = 2 these imply
More generally,[13] for positive m (See Hermite's identity)
The following can be used to convert floors to ceilings and vice versa (m positive)[14]
For all m and n strictly positive integers:[15]
which, for positive and coprime m and n, reduces to
and similarly for the ceiling and fractional part functions (still for positive and coprime m and n),
Since the right-hand side of the general case is symmetrical in m and n, this implies that
More generally, if m and n are positive,
This is sometimes called a reciprocity law.[16]
Division by positive integers gives rise to an interesting and sometimes useful property. Assuming ,
Similarly,
Indeed,
keeping in mind that The second equivalence involving the ceiling function can be proved similarly.
Nested divisions edit
For positive integer n, and arbitrary real numbers m,x:[17]
Continuity and series expansions edit
None of the functions discussed in this article are continuous, but all are piecewise linear: the functions , , and have discontinuities at the integers.
is upper semi-continuous and and are lower semi-continuous.
Since none of the functions discussed in this article are continuous, none of them have a power series expansion. Since floor and ceiling are not periodic, they do not have uniformly convergent Fourier series expansions. The fractional part function has Fourier series expansion[18]
for x not an integer.
At points of discontinuity, a Fourier series converges to a value that is the average of its limits on the left and the right, unlike the floor, ceiling and fractional part functions: for y fixed and x a multiple of y the Fourier series given converges to y/2, rather than to x mod y = 0. At points of continuity the series converges to the true value.
Using the formula floor(x) = x − {x} gives
for x not an integer.
Applications edit
Mod operator edit
For an integer x and a positive integer y, the modulo operation, denoted by x mod y, gives the value of the remainder when x is divided by y. This definition can be extended to real x and y, y ≠ 0, by the formula
Then it follows from the definition of floor function that this extended operation satisfies many natural properties. Notably, x mod y is always between 0 and y, i.e.,
if y is positive,
and if y is negative,
Quadratic reciprocity edit
Gauss's third proof of quadratic reciprocity, as modified by Eisenstein, has two basic steps.[19][20]
Let p and q be distinct positive odd prime numbers, and let
First, Gauss's lemma is used to show that the Legendre symbols are given by
The second step is to use a geometric argument to show that
Combining these formulas gives quadratic reciprocity in the form
There are formulas that use floor to express the quadratic character of small numbers mod odd primes p:[21]
Rounding edit
For an arbitrary real number , rounding to the nearest integer with tie breaking towards positive infinity is given by ; rounding towards negative infinity is given as .
If tie-breaking is away from 0, then the rounding function is (see sign function), and rounding towards even can be expressed with the more cumbersome , which is the above expression for rounding towards positive infinity minus an integrality indicator for .
Rounding a real number to the nearest integer value forms a very basic type of quantizer – a uniform one. A typical (mid-tread) uniform quantizer with a quantization step size equal to some value can be expressed as
- ,
Number of digits edit
The number of digits in base b of a positive integer k is
Number of strings without repeated characters edit
The number of possible strings of arbitrary length that doesn't use any character twice is given by[22][better source needed]
where:
- n > 0 is the number of letters in the alphabet (e.g., 26 in English)
- the falling factorial denotes the number of strings of length k that don't use any character twice.
- n! denotes the factorial of n
- e = 2.718... is Euler's number
For n = 26, this comes out to 1096259850353149530222034277.
Factors of factorials edit
Let n be a positive integer and p a positive prime number. The exponent of the highest power of p that divides n! is given by a version of Legendre's formula[23]
where is the way of writing n in base p. This is a finite sum, since the floors are zero when pk > n.
Beatty sequence edit
The Beatty sequence shows how every positive irrational number gives rise to a partition of the natural numbers into two sequences via the floor function.[24]
Euler's constant (γ) edit
There are formulas for Euler's constant γ = 0.57721 56649 ... that involve the floor and ceiling, e.g.[25]
and
Riemann zeta function (ζ) edit
The fractional part function also shows up in integral representations of the Riemann zeta function. It is straightforward to prove (using integration by parts)[26] that if is any function with a continuous derivative in the closed interval [a, b],
Letting for real part of s greater than 1 and letting a and b be integers, and letting b approach infinity gives
This formula is valid for all s with real part greater than −1, (except s = 1, where there is a pole) and combined with the Fourier expansion for {x} can be used to extend the zeta function to the entire complex plane and to prove its functional equation.[27]
For s = σ + it in the critical strip 0 < σ < 1,
In 1947 van der Pol used this representation to construct an analogue computer for finding roots of the zeta function.[28]
Formulas for prime numbers edit
The floor function appears in several formulas characterizing prime numbers. For example, since is equal to 1 if m divides n, and to 0 otherwise, it follows that a positive integer n is a prime if and only if[29]
One may also give formulas for producing the prime numbers. For example, let pn be the n-th prime, and for any integer r > 1, define the real number α by the sum
Then[30]
A similar result is that there is a number θ = 1.3064... (Mills' constant) with the property that
are all prime.[31]
There is also a number ω = 1.9287800... with the property that
are all prime.[31]
Let π(x) be the number of primes less than or equal to x. It is a straightforward deduction from Wilson's theorem that[32]
Also, if n ≥ 2,[33]
None of the formulas in this section are of any practical use.[34][35]
Solved problems edit
Ramanujan submitted these problems to the Journal of the Indian Mathematical Society.[36]
If n is a positive integer, prove that
Some generalizations to the above floor function identities have been proven.[37]
Unsolved problem edit
The study of Waring's problem has led to an unsolved problem:
Are there any positive integers k ≥ 6 such that[38]
Mahler has proved there can only be a finite number of such k; none are known.[39]
Computer implementations edit
In most programming languages, the simplest method to convert a floating point number to an integer does not do floor or ceiling, but truncation. The reason for this is historical, as the first machines used ones' complement and truncation was simpler to implement (floor is simpler in two's complement). FORTRAN was defined to require this behavior and thus almost all processors implement conversion this way. Some consider this to be an unfortunate historical design decision that has led to bugs handling negative offsets and graphics on the negative side of the origin.[citation needed]
An arithmetic right-shift of a signed integer by is the same as . Division by a power of 2 is often written as a right-shift, not for optimization as might be assumed, but because the floor of negative results is required. Assuming such shifts are "premature optimization" and replacing them with division can break software.[citation needed]
Many programming languages (including C, C++,[40][41] C#,[42][43] Java,[44][45] PHP,[46][47] R,[48] and Python[49]) provide standard functions for floor and ceiling, usually called floor and ceil, or less commonly ceiling.[50] The language APL uses ⌊x for floor. The J Programming Language, a follow-on to APL that is designed to use standard keyboard symbols, uses <. for floor and >. for ceiling.[51]
ALGOL usesentier for floor.
In Microsoft Excel the funtion INT rounds down rather than toward zero,[52] while FLOOR rounds toward zero, the opposite of what "int" and "floor" do in other languages. Since 2010 FLOOR has been changed to error if the number is negative.[53] The OpenDocument file format, as used by OpenOffice.org, Libreoffice and others, INT[54] and FLOOR both do floor, and FLOOR has a third argument to reproduce Excel's earlier behavior.[55]
See also edit
Citations edit
- ^ Graham, Knuth, & Patashnik, Ch. 3.1
- ^
1) Luke Heaton, A Brief History of Mathematical Thought, 2015, ISBN 1472117158 (n.p.)
2) Albert A. Blank et al., Calculus: Differential Calculus, 1968, p. 259
3) John W. Warris, Horst Stocker, Handbook of mathematics and computational science, 1998, ISBN 0387947469, p. 151 - ^ Lemmermeyer, pp. 10, 23.
- ^ e.g. Cassels, Hardy & Wright, and Ribenboim use Gauss's notation. Graham, Knuth & Patashnik, and Crandall & Pomerance use Iverson's.
- ^ Iverson, p. 12.
- ^ Higham, p. 25.
- ^ Mathwords: Floor Function.
- ^ Mathwords: Ceiling Function
- ^ Graham, Knuth, & Patashnik, p. 70.
- ^ Graham, Knuth, & Patashink, Ch. 3
- ^ Graham, Knuth, & Patashnik, p. 73
- ^ Graham, Knuth, & Patashnik, p. 85
- ^ Graham, Knuth, & Patashnik, p. 85 and Ex. 3.15
- ^ Graham, Knuth, & Patashnik, Ex. 3.12
- ^ Graham, Knuth, & Patashnik, p. 94.
- ^ Graham, Knuth, & Patashnik, p. 94
- ^ Graham, Knuth, & Patashnik, p. 71, apply theorem 3.10 with x/m as input and the division by n as function
- ^ Titchmarsh, p. 15, Eq. 2.1.7
- ^ Lemmermeyer, § 1.4, Ex. 1.32–1.33
- ^ Hardy & Wright, §§ 6.11–6.13
- ^ Lemmermeyer, p. 25
- ^ OEIS sequence A000522 (Total number of arrangements of a set with n elements: a(n) = Sum_{k=0..n} n!/k!.) (See Formulas.)
- ^ Hardy & Wright, Th. 416
- ^ Graham, Knuth, & Patashnik, pp. 77–78
- ^ These formulas are from the Wikipedia article Euler's constant, which has many more.
- ^ Titchmarsh, p. 13
- ^ Titchmarsh, pp.14–15
- ^ Crandall & Pomerance, p. 391
- ^ Crandall & Pomerance, Ex. 1.3, p. 46. The infinite upper limit of the sum can be replaced with n. An equivalent condition is n > 1 is prime if and only if .
- ^ Hardy & Wright, § 22.3
- ^ a b Ribenboim, p. 186
- ^ Ribenboim, p. 181
- ^ Crandall & Pomerance, Ex. 1.4, p. 46
- ^ Ribenboim, p. 180 says that "Despite the nil practical value of the formulas ... [they] may have some relevance to logicians who wish to understand clearly how various parts of arithmetic may be deduced from different axiomatzations ... "
- ^ Hardy & Wright, pp. 344—345 "Any one of these formulas (or any similar one) would attain a different status if the exact value of the number α ... could be expressed independently of the primes. There seems no likelihood of this, but it cannot be ruled out as entirely impossible."
- ^ Ramanujan, Question 723, Papers p. 332
- ^ Somu, Sai Teja; Kukla, Andrzej (2022). "On some generalizations to floor function identities of Ramanujan" (PDF). Integers. 22. arXiv:2109.03680.
- ^ Hardy & Wright, p. 337
- ^ Mahler, Kurt (1957). "On the fractional parts of the powers of a rational number II". Mathematika. 4 (2): 122–124. doi:10.1112/S0025579300001170.
- ^ "C++ reference of
floorfunction". Retrieved 5 December 2010. - ^ "C++ reference of
ceilfunction". Retrieved 5 December 2010. - ^ dotnet-bot. "Math.Floor Method (System)". docs.microsoft.com. Retrieved 28 November 2019.
- ^ dotnet-bot. "Math.Ceiling Method (System)". docs.microsoft.com. Retrieved 28 November 2019.
- ^ "Math (Java SE 9 & JDK 9 )". docs.oracle.com. Retrieved 20 November 2018.
- ^ "Math (Java SE 9 & JDK 9 )". docs.oracle.com. Retrieved 20 November 2018.
- ^ "PHP manual for
ceilfunction". Retrieved 18 July 2013. - ^ "PHP manual for
floorfunction". Retrieved 18 July 2013. - ^ "R: Rounding of Numbers".
- ^ "Python manual for
mathmodule". Retrieved 18 July 2013. - ^ Sullivan, p. 86.
- ^ "Vocabulary". J Language. Retrieved 6 September 2011.
- ^ "INT function". Retrieved 29 October 2021.
- ^ "FLOOR function". Retrieved 29 October 2021.
- ^ "Documentation/How Tos/Calc: INT function". Retrieved 29 October 2021.
- ^ "Documentation/How Tos/Calc: FLOOR function". Retrieved 29 October 2021.
References edit
- J.W.S. Cassels (1957), An introduction to Diophantine approximation, Cambridge Tracts in Mathematics and Mathematical Physics, vol. 45, Cambridge University Press
- Crandall, Richard; Pomerance, Carl (2001), Prime Numbers: A Computational Perspective, New York: Springer, ISBN 0-387-94777-9
- Graham, Ronald L.; Knuth, Donald E.; Patashnik, Oren (1994), Concrete Mathematics, Reading Ma.: Addison-Wesley, ISBN 0-201-55802-5
- Hardy, G. H.; Wright, E. M. (1980), An Introduction to the Theory of Numbers (Fifth edition), Oxford: Oxford University Press, ISBN 978-0-19-853171-5
- Nicholas J. Higham, Handbook of writing for the mathematical sciences, SIAM. ISBN 0-89871-420-6, p. 25
- ISO/IEC. ISO/IEC 9899::1999(E): Programming languages — C (2nd ed), 1999; Section 6.3.1.4, p. 43.
- Iverson, Kenneth E. (1962), A Programming Language, Wiley
- Lemmermeyer, Franz (2000), Reciprocity Laws: from Euler to Eisenstein, Berlin: Springer, ISBN 3-540-66957-4
- Ramanujan, Srinivasa (2000), Collected Papers, Providence RI: AMS / Chelsea, ISBN 978-0-8218-2076-6
- Ribenboim, Paulo (1996), The New Book of Prime Number Records, New York: Springer, ISBN 0-387-94457-5
- Michael Sullivan. Precalculus, 8th edition, p. 86
- Titchmarsh, Edward Charles; Heath-Brown, David Rodney ("Roger") (1986), The Theory of the Riemann Zeta-function (2nd ed.), Oxford: Oxford U. P., ISBN 0-19-853369-1
External links edit
- "Floor function", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Štefan Porubský, "Integer rounding functions", Interactive Information Portal for Algorithmic Mathematics, Institute of Computer Science of the Czech Academy of Sciences, Prague, Czech Republic, retrieved 24 October 2008
- Weisstein, Eric W. "Floor Function". MathWorld.
- Weisstein, Eric W. "Ceiling Function". MathWorld.


