Uniform heptagonal antiprism
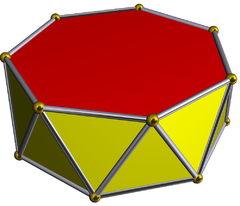
Type	Prismatic uniform polyhedron
Elements	F = 16, E = 28 V = 14 (χ = 2)
Faces by sides	14{3}+2{7}
Schläfli symbol	s{2,14} sr{2,7}
Wythoff symbol	| 2 2 7
Coxeter diagram
Symmetry group	D7d, [2+,14], (2*7), order 28
Rotation group	D7, [7,2]+, (722), order 14
References	U77(e)
Dual	Heptagonal trapezohedron
Properties	convex
Vertex figure 3.3.3.7

In geometry, the heptagonal antiprism is the fifth in an infinite set of antiprisms formed by two parallel polygons separated by a strip of triangles. In the case of the heptagonal antiprism, the caps are two regular heptagons. As a result, this polyhedron has 14 vertices, and 14 equilateral triangle faces. There are 14 edges where a triangle meets a heptagon, and another 14 edges where two triangles meet.

The heptagonal antiprism was first depicted by Johannes Kepler, as an example of the general construction of antiprisms.^[1]