
Summary
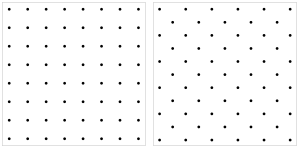
| |
| Upright square Simple |
diagonal square Centered |
|---|---|
In mathematics, the square lattice is a type of lattice in a two-dimensional Euclidean space. It is the two-dimensional version of the integer lattice, denoted as .[1] It is one of the five types of two-dimensional lattices as classified by their symmetry groups;[2] its symmetry group in IUC notation as p4m,[3] Coxeter notation as [4,4],[4] and orbifold notation as *442.[5]

Two orientations of an image of the lattice are by far the most common. They can conveniently be referred to as the upright square lattice and diagonal square lattice; the latter is also called the centered square lattice.[6] They differ by an angle of 45°. This is related to the fact that a square lattice can be partitioned into two square sub-lattices, as is evident in the colouring of a checkerboard.
Symmetry edit
The square lattice's symmetry category is wallpaper group p4m. A pattern with this lattice of translational symmetry cannot have more, but may have less symmetry than the lattice itself. An upright square lattice can be viewed as a diagonal square lattice with a mesh size that is √2 times as large, with the centers of the squares added. Correspondingly, after adding the centers of the squares of an upright square lattice one obtains a diagonal square lattice with a mesh size that is √2 times as small as that of the original lattice. A pattern with 4-fold rotational symmetry has a square lattice of 4-fold rotocenters that is a factor √2 finer and diagonally oriented relative to the lattice of translational symmetry.
With respect to reflection axes there are three possibilities:
- None. This is wallpaper group p4.
- In four directions. This is wallpaper group p4m.
- In two perpendicular directions. This is wallpaper group p4g. The points of intersection of the reflexion axes form a square grid which is as fine as, and oriented the same as, the square lattice of 4-fold rotocenters, with these rotocenters at the centers of the squares formed by the reflection axes.
| p4, [4,4]+, (442) | p4g, [4,4+], (4*2) | p4m, [4,4], (*442) |
|---|---|---|
| Wallpaper group p4, with the arrangement within a primitive cell of the 2- and 4-fold rotocenters (also applicable for p4g and p4m). Fundamental domain
|
Wallpaper group p4g. There are reflection axes in two directions, not through the 4-fold rotocenters. Fundamental domain
|
Wallpaper group p4m. There are reflection axes in four directions, through the 4-fold rotocenters. In two directions the reflection axes are oriented the same as, and as dense as, those for p4g, but shifted. In the other two directions they are linearly a factor √2 denser. Fundamental domain
|
Crystal classes edit
The square lattice class names, Schönflies notation, Hermann-Mauguin notation, orbifold notation, Coxeter notation, and wallpaper groups are listed in the table below.
| Geometric class, point group | Wallpaper groups | ||||
|---|---|---|---|---|---|
| Schön. | Intl | Orb. | Cox. | ||
| C4 | 4 | (44) | [4]+ | p4 (442) |
|
| D4 | 4mm | (*44) | [4] | p4m (*442) |
p4g (4*2) |
See also edit
References edit
- ^ Conway, John; Sloane, Neil J. A. (1999), Sphere Packings, Lattices and Groups, Springer, p. 106, ISBN 9780387985855.
- ^ Golubitsky, Martin; Stewart, Ian (2003), The Symmetry Perspective: From Equilibrium to Chaos in Phase Space and Physical Space, Progress in Mathematics, vol. 200, Springer, p. 129, ISBN 9783764321710.
- ^ Field, Michael; Golubitsky, Martin (2009), Symmetry in Chaos: A Search for Pattern in Mathematics, Art, and Nature (2nd ed.), SIAM, p. 47, ISBN 9780898717709.
- ^ Johnson, Norman W.; Weiss, Asia Ivić (1999), "Quadratic integers and Coxeter groups", Canadian Journal of Mathematics, 51 (6): 1307–1336, doi:10.4153/CJM-1999-060-6. See in particular the top of p. 1320.
- ^ Schattschneider, Doris; Senechal, Marjorie (2004), "Tilings", in Goodman, Jacob E.; O'Rourke, Joseph (eds.), Handbook of Discrete and Computational Geometry, Discrete Mathematics and Its Applications (2nd ed.), CRC Press, pp. 53–72, ISBN 9781420035315. See in particular the table on p. 62 relating IUC notation to orbifold notation.
- ^ Johnston, Bernard L.; Richman, Fred (1997), Numbers and Symmetry: An Introduction to Algebra, CRC Press, p. 159, ISBN 9780849303012.



