Uniform pentagrammic antiprism
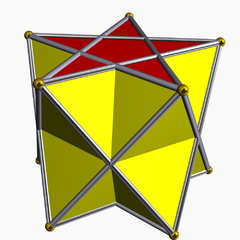
Type	Prismatic uniform polyhedron
Elements	F = 12, E = 20 V = 10 (χ = 2)
Faces by sides	10{3}+2{5/2}
Schläfli symbol	sr{2,5/2}
Wythoff symbol	| 2 2 5/2
Coxeter diagram
Symmetry	D5h, [5,2], (*552), order 20
Rotation group	D5, [5,2]+, (55), order 10
Index references	U79(a)
Dual	Pentagrammic trapezohedron
Properties	nonconvex
Vertex figure 3.3.3.5/2

In geometry, the pentagrammic antiprism is one in an infinite set of nonconvex antiprisms formed by triangle sides and two regular star polygon caps, in this case two pentagrams.

It has 12 faces, 20 edges and 10 vertices. This polyhedron is identified with the indexed name U₇₉ as a uniform polyhedron.^[1]

Note that the pentagram face has an ambiguous interior because it is self-intersecting. The central pentagon region can be considered interior or exterior depending on how interior is defined. One definition of interior is the set of points that have a ray that crosses the boundary an odd number of times to escape the perimeter.

In either case, it is best to show the pentagram boundary line to distinguish it from a concave decagon.