
Summary
In mathematics, the slope or gradient of a line is a number that describes both the direction and the steepness of the line.[1] Slope is often denoted by the letter m; there is no clear answer to the question why the letter m is used for slope, but its earliest use in English appears in O'Brien (1844)[2] who wrote the equation of a straight line as "y = mx + b" and it can also be found in Todhunter (1888)[3] who wrote it as "y = mx + c".[4]
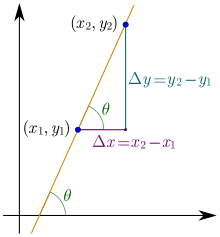
Slope is calculated by finding the ratio of the "vertical change" to the "horizontal change" between (any) two distinct points on a line. Sometimes the ratio is expressed as a quotient ("rise over run"), giving the same number for every two distinct points on the same line. A line that is decreasing has a negative "rise". The line may be practical – as set by a road surveyor, or in a diagram that models a road or a roof either as a description or as a plan.
The steepness, incline, or grade of a line is measured by the absolute value of the slope. A slope with a greater absolute value indicates a steeper line. The direction of a line is either increasing, decreasing, horizontal or vertical.
- A line is increasing if it goes up from left to right. The slope is positive, i.e. .
- A line is decreasing if it goes down from left to right. The slope is negative, i.e. .
- If a line is horizontal the slope is zero. This is a constant function.
- If a line is vertical the slope is undefined (see below).
The rise of a road between two points is the difference between the altitude of the road at those two points, say y1 and y2, or in other words, the rise is (y2 − y1) = Δy. For relatively short distances, where the Earth's curvature may be neglected, the run is the difference in distance from a fixed point measured along a level, horizontal line, or in other words, the run is (x2 − x1) = Δx. Here the slope of the road between the two points is simply described as the ratio of the altitude change to the horizontal distance between any two points on the line.
In mathematical language, the slope m of the line is
The concept of slope applies directly to grades or gradients in geography and civil engineering. Through trigonometry, the slope m of a line is related to its angle of inclination θ by the tangent function
Thus, a 45° rising line has a slope of +1 and a 45° falling line has a slope of −1.
As a generalization of this practical description, the mathematics of differential calculus defines the slope of a curve at a point as the slope of the tangent line at that point. When the curve is given by a series of points in a diagram or in a list of the coordinates of points, the slope may be calculated not at a point but between any two given points. When the curve is given as a continuous function, perhaps as an algebraic expression, then the differential calculus provides rules giving a formula for the slope of the curve at any point in the middle of the curve.
This generalization of the concept of slope allows very complex constructions to be planned and built that go well beyond static structures that are either horizontals or verticals, but can change in time, move in curves, and change depending on the rate of change of other factors. Thereby, the simple idea of slope becomes one of the main basis of the modern world in terms of both technology and the built environment.
Definition edit
The slope of a line in the plane containing the x and y axes is generally represented by the letter m,[5] and is defined as the change in the y coordinate divided by the corresponding change in the x coordinate, between two distinct points on the line. This is described by the following equation:
(The Greek letter delta, Δ, is commonly used in mathematics to mean "difference" or "change".)
Given two points and , the change in from one to the other is (run), while the change in is (rise). Substituting both quantities into the above equation generates the formula:
The formula fails for a vertical line, parallel to the axis (see Division by zero), where the slope can be taken as infinite, so the slope of a vertical line is considered undefined.
Examples edit
Suppose a line runs through two points: P = (1, 2) and Q = (13, 8). By dividing the difference in -coordinates by the difference in -coordinates, one can obtain the slope of the line:
- Since the slope is positive, the direction of the line is increasing. Since |m| < 1, the incline is not very steep (incline < 45°).
As another example, consider a line which runs through the points (4, 15) and (3, 21). Then, the slope of the line is
- Since the slope is negative, the direction of the line is decreasing. Since |m| > 1, this decline is fairly steep (decline > 45°).
Algebra and geometry edit
- If is a linear function of , then the coefficient of is the slope of the line created by plotting the function. Therefore, if the equation of the line is given in the form
- If the slope of a line and a point on the line are both known, then the equation of the line can be found using the point-slope formula:
- The slope of the line defined by the linear equation
- .
- Two lines are parallel if and only if they are not the same line (coincident) and either their slopes are equal or they both are vertical and therefore both have undefined slopes.
- Two lines are perpendicular if the product of their slopes is −1 or one has a slope of 0 (a horizontal line) and the other has an undefined slope (a vertical line).
- The angle θ between −90° and 90° that a line makes with the x-axis is related to the slope m as follows:
- (this is the inverse function of tangent; see inverse trigonometric functions).
Examples edit
For example, consider a line running through points (2,8) and (3,20). This line has a slope, m, of
One can then write the line's equation, in point-slope form:
or:
The angle θ between −90° and 90° that this line makes with the x-axis is
Consider the two lines: y = −3x + 1 and y = −3x − 2. Both lines have slope m = −3. They are not the same line. So they are parallel lines.
Consider the two lines y = −3x + 1 and y = x/3 − 2. The slope of the first line is m1 = −3. The slope of the second line is m2 = 1/3. The product of these two slopes is −1. So these two lines are perpendicular.
Statistics edit
In statistics, the gradient of the least-squares regression best-fitting line for a given sample of data may be written as:
- ,
This quantity m is called as the regression slope for the line . The quantity is Pearson's correlation coefficient, is the standard deviation of the y-values and is the standard deviation of the x-values. This may also be written as a ratio of covariances:[6]
Slope of a road or railway edit
There are two common ways to describe the steepness of a road or railroad. One is by the angle between 0° and 90° (in degrees), and the other is by the slope in a percentage. See also steep grade railway and rack railway.
The formulae for converting a slope given as a percentage into an angle in degrees and vice versa are:
- (this is the inverse function of tangent; see trigonometry)
and
where angle is in degrees and the trigonometric functions operate in degrees. For example, a slope of 100% or 1000‰ is an angle of 45°.
A third way is to give one unit of rise in say 10, 20, 50 or 100 horizontal units, e.g. 1:10. 1:20, 1:50 or 1:100 (or "1 in 10", "1 in 20", etc.) 1:10 is steeper than 1:20. For example, steepness of 20% means 1:5 or an incline with angle 11.3°.
Roads and railways have both longitudinal slopes and cross slopes.
-
Slope warning sign in the Netherlands
-
Slope warning sign in Poland
-
A 1371-meter distance of a railroad with a 20‰ slope. Czech Republic
-
Steam-age railway gradient post indicating a slope in both directions at Meols railway station, United Kingdom
Calculus edit
The concept of a slope is central to differential calculus. For non-linear functions, the rate of change varies along the curve. The derivative of the function at a point is the slope of the line tangent to the curve at the point, and is thus equal to the rate of change of the function at that point.
If we let Δx and Δy be the distances (along the x and y axes, respectively) between two points on a curve, then the slope given by the above definition,
- ,
is the slope of a secant line to the curve. For a line, the secant between any two points is the line itself, but this is not the case for any other type of curve.
For example, the slope of the secant intersecting y = x2 at (0,0) and (3,9) is 3. (The slope of the tangent at x = 3⁄2 is also 3 − a consequence of the mean value theorem.)
By moving the two points closer together so that Δy and Δx decrease, the secant line more closely approximates a tangent line to the curve, and as such the slope of the secant approaches that of the tangent. Using differential calculus, we can determine the limit, or the value that Δy/Δx approaches as Δy and Δx get closer to zero; it follows that this limit is the exact slope of the tangent. If y is dependent on x, then it is sufficient to take the limit where only Δx approaches zero. Therefore, the slope of the tangent is the limit of Δy/Δx as Δx approaches zero, or dy/dx. We call this limit the derivative.
The value of the derivative at a specific point on the function provides us with the slope of the tangent at that precise location. For example, let y = x2. A point on this function is (−2,4). The derivative of this function is dy⁄dx = 2x. So the slope of the line tangent to y at (−2,4) is 2 ⋅ (−2) = −4. The equation of this tangent line is: y − 4 = (−4)(x − (−2)) or y = −4x − 4.
Difference of slopes edit
An extension of the idea of angle follows from the difference of slopes. Consider the shear mapping
Then is mapped to . The slope of is zero and the slope of is . The shear mapping added a slope of . For two points on with slopes and , the image
has slope increased by , but the difference of slopes is the same before and after the shear. This invariance of slope differences makes slope an angular invariant measure, on a par with circular angle (invariant under rotation) and hyperbolic angle, with invariance group of squeeze mappings.[7][8]
Other uses edit
The concept of a slope or gradient is also used as a basis for developing other applications in mathematics:
- Gradient descent, a first-order iterative optimization algorithm for finding the minimum of a function
- Gradient theorem, theorem that a line integral through a gradient field can be evaluated by evaluating the original scalar field at the endpoints of the curve
- Gradient method, an algorithm to solve problems with search directions defined by the gradient of the function at the current point
- Conjugate gradient method, an algorithm for the numerical solution of particular systems of linear equations
- Nonlinear conjugate gradient method, generalizes the conjugate gradient method to nonlinear optimization
- Stochastic gradient descent, iterative method for optimizing a differentiable objective function
See also edit
- Euclidean distance
- Grade
- Inclined plane
- Linear function
- Line of greatest slope
- Mediant
- Slope definitions
- Theil–Sen estimator, a line with the median slope among a set of sample points
References edit
- ^ Clapham, C.; Nicholson, J. (2009). "Oxford Concise Dictionary of Mathematics, Gradient" (PDF). Addison-Wesley. p. 348. Archived from the original (PDF) on 29 October 2013. Retrieved 1 September 2013.
- ^ O'Brien, M. (1844), A Treatise on Plane Co-Ordinate Geometry or the Application of the Method of Co-Ordinates in the Solution of Problems in Plane Geometry, Cambridge, England: Deightons
- ^ Todhunter, I. (1888), Treatise on Plane Co-Ordinate Geometry as Applied to the Straight Line and Conic Sections, London: Macmillan
- ^ Weisstein, Eric W. "Slope". MathWorld--A Wolfram Web Resource. Archived from the original on 6 December 2016. Retrieved 30 October 2016.
- ^ An early example of this convention can be found in Salmon, George (1850). A Treatise on Conic Sections (2nd ed.). Dublin: Hodges and Smith. pp. 14–15.
- ^ Further Mathematics Units 3&4 VCE (Revised). Cambridge Senior Mathematics. 2016. ISBN 9781316616222 – via Physical Copy.
- ^ Bolt, Michael; Ferdinands, Timothy; Kavlie, Landon (2009). "The most general planar transformations that map parabolas into parabolas". Involve: A Journal of Mathematics. 2 (1): 79–88. doi:10.2140/involve.2009.2.79. ISSN 1944-4176.
- ^ Abstract Algebra/Shear and Slope at Wikibooks
External links edit
- "Slope of a Line (Coordinate Geometry)". Math Open Reference. 2009. Retrieved 30 October 2016. interactive







